Testsida

Från Wikiskola
Hoppa till navigering Hoppa till sök

Inledning

här testar jag transclusion för att göra en mattebok. Tanken är att varje moment typ procentbegreppet ska bli en lektionsmodul och ett lärobjekt.

Procentdelen 4.4 anv transclusion med sidan procent år 7 som innehåller taggen vilket innebär att det bra blir en del av sidan transcluderad.

Tal och räkning

Planer

Övningar tal och räkning 6A

Övningar tal och räkning 6B

Film.


Välkomna till en ny termin!

Först ska vi gå igenom Mina klassrumsregeler som handlar om hur jag vill ha det i klassrummet. Jag hoppas att alla håller med. Dessa regler gäller i alla sammanhang, oavsett om det är no, matte eler mentorstid.

När det gäller undervisningen i matte kommer det att se ut som förra året.

  • Information på wikiskola.se
  • bloggarna
  • resultat i infomenor
  • Läxor varje vecka utom när det är prov
  • Beting
  • Vi kommer ofta att arbeta utanför boken. Det kan vara laborationer, praktiska uppgifter, stenciler, spel, datorövningar, mattekluringar, känguru, skrivövningar, etc. Nytt för i år är halvklasslektioner i 7F.
  • Prov men förhoppningsvis även andra kunskapskontroller.
  • Möjlighet att göra prov för år 8.

Planer

Lektion 1 aritmetik år 7

Uppgift nr 9

Placering

Ni får skrivhäften, läxhäften och er mattebok.

Det går bra att börja räkna från sidan 8.

Den som mmissat diagnosen får göra den nu.

Vi avrundar med att lösa uppgift 9 på tavlan.

Kortfilm. Begreppen addition, subtraktion, multiplikation .. förklaras


Lektion 3 Decimaler

decimaltal

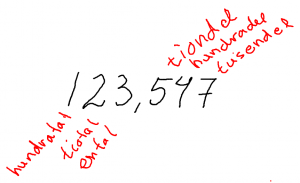
Vi tittar på arbetsplanen och vi väljer beting.

Decimaler är på sidan 12-13 i boken.

Se en kortfilm. Decimaler på Kunskapshubben

Uppgift Hur många centimeter är 2,375 meter?


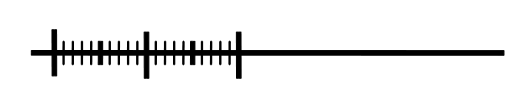
Lektion 4 - tallinjen

Mål. Förstå hur tiossystemet funkar - talsystemet

Introduktion: Vi ritar en tallinje på tavlan. Den sträcker sig från 1-100. Man kan sätta ett halvtjockt streck vid 50. elle ett var tionde. Sedan små streck för ental om man kunde förstora den. Låt eleverna komma fram och rita in tal. Tar det stopp? Zooma. Hur många tal finns det?

En annan från 1-10.

En tredje från 0-1.

  • Nu kan ni komma fram en och en och sätta ut tal på tallinjen

Datorövning: En övning i att rita tallinjer i powerpoint.

Räkneuppgifter till tallinjen på sidan 14-15 i matteDirekt år 7.

Datorövning. Matteva - storleksordna tal

Lektion 5 - Multiplicera och dividera med 10, 100, 1000, ...

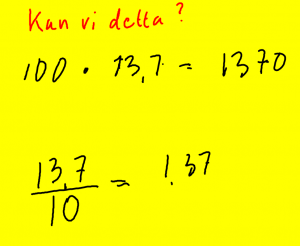
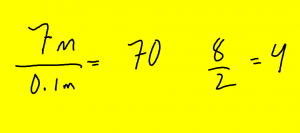
Mål: Multiplikation och division med 10, 100, 1000

Förmodligen kan du multiplicera med 10, 100 och tusen om det är heltal. 

 10* 15 = 150. man lägger till en nolla.

På samma sätt vet du hur man delar med 10 osv. 

 3700 / 100 = 37. Ta bort nollor.

Om det är decimaltal så flyttar du decimaltecknet. 

 10 * 37,5 = 375
 37,5 / 10 = 3,75

Räkna själv. MatteDirekt år 7, sid 16-17.

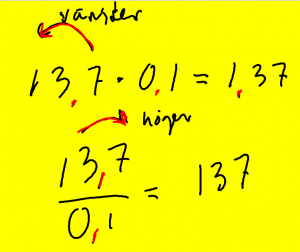
Men vad händer om du multiplicerar eller dividerar med 0,1 0,01 eller 0,001?

Det ser du på bilden till vänster.

Mål över G: Multiplikation och division med 0,1, 0,01, 0,001

  • Läsanvisning: Tetra B sid 8-11 (Stencil)

Datorövning. Multiplicera och dividera med 10, 100, 1000

Lektion 6 - Enheter

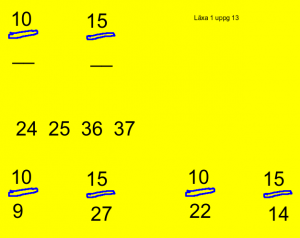
Uppföljning till läxa 1. Diskutera uppgifterna 6b och 13 på tavlan. Du ser dem här bredvid.

Längdenheter

Fundera på omdu kan alla dessa omvandlingar. 

 1 m = 10 dm = 100 cm = 1 000 mm = 1 000 000 mikrometer
 0,001 m = 1 mm  |  0,01 m = 1 cm  |  0,1 m = 1 dm
 1 km = 1000 m   |  10 km = 1 mil

Konvertera.nu

Titta på denna sida och svara på frågorna: konvertera.nu

Klicka på länken Volym. Välj sedan Signifikanta siffror 1. Då blir det en decimal. Testa att skriva 1 på liter och klicka utanför rutorna.

  1. Volym: Hur många centiliter går det på en liter?
  2. Volym. Hur många ml är en kubikcentimeter?
  3. Längd. Hur många meter är 1,2 km?
  4. Längd. Hur många nanomater går det på en mikrometer?

SI-enheter på wikipedia

Räkna själv:

Lektion 7 - Avrundning

Enkelt uttryckt. 1,2,3,4 avrundas nedåt. 6, 7, 8, 9 avrundas uppåt. numera avrundas femman uppåt men när jag lärde mig matte fanns det en krångligare regel så därför händer det att jag tvekar på detta. Så djupt sitter det man drillats i.

Mål: Kunna avrunda heltal och decimaltal

Datorövning från Matteva. Avrundning

  • MatteDirekt år 7, sid 10.
  • Matematikboken X sid 19-20 (stencil).

Lektion 8 - Överslagsräkning

Mål: Överslagsräkning

Gemensam övning

Räkna själv

  • Röd kurs sidorna 34-35 i matteDirekt.
  • (Matematikboken X sid 21-25 (stencil i pärmen).)

Datorövning. Matteva - uppskattning

Repetition

Inledning

Vi har nu gått igeneom alla delar som ingår i grundkursen för år 7. Nu ska vi testa vad ni kan och sedan ska ni få öva mer på det ni behöver öva mer på. beroende på hur långt ni kommit finns det två alternativ för vad ni ska göra. endast ett gäller.

Antingen gör ni diagnosen.

Eller så gör ni Repetitionsuppgifter på stencil.

Avslutning. Vad behöver vi jobba mer med?

Repetition 2

Genomgång läxa 2: uppgifterna 10 och 13.

Det blir inget extraprov på detta kapitel.

Jobba färdigt med diagnosen eller repetitionsuppgifterna.

Kluring. Vi vet att man kan testa om ett tal är delbart med tre genom att undersöka om siffersumman är delbar med tre. Men hur kan det vara så. Fundera ut en förklaring och blogga den.

Därefter:

  • blå kurs eller röd kurs beroende på diagnosen

Lektion 9 - Faktorisering

Genomgång läxa 3: uppgifterna 6B ? och 10.

Mål: Kunna faktorisera tvåsiffriga tal.


  • Memoryspel för att öva på att känna igen faktoriseringar. Memory kan säkert användas till en mängd övningar. I detta fall har jag gjort mallen i ppt där man printar åhörarkopior med sex bilder per sida. Varje bild är ett kort som man kan klippa ut och plasta in.
  • Uppgift. Du ska hitta på en matteuppgift. Den ska vara av typen - faktorisera talet xx. Du ska bestämma vad xx är för ett tal. Gör uppgiften svår genom att hitta på ett klurigt xx-tal. Alltså, hitta på det svåraste talet mellan 1-100 att faktorisera. Testa det på en kompis.

Datorövninga från matteva. http://www.skolresurs.fi/matteva/taluppfattning/faktorisering.html Faktorisering

Utmaning: spela 21

Lektion 10 Primtal

Mål: Veta vad ett primtal är och hur man undersöker om ett tal är ett primtal.

  • Spela Kenken. Där inser du att det kan vara bra att lära sig faktorisering.
  • MatteDirekt år 7 sid 38-39.
  • Hitta-primtalsspel med tärningar vilket jag kallat kryssa fullt. Poängen med spelet är att ....som vi förstår att ... vill inte avslöja mer.
  • Wikipedia förkarar Eratosthenes såll och jag lade till några uppgifter.
  • Matte Direkt sidan 41 om Eratosthenes beräkning av jordradien.
  • Pröva gärna att använda Excel för att undersöka om ett tal är ett primtal.

Datorövning. Lär dig mer om ett tal genom WolframAlpha. Du ser bland annat hur talet delas upp i faktorer. Skriv bara talet på raden och klicka enter.

Datorövninga från matteva. Delbarhetsreglerna

  • Här kan det vara bra att känna till att:
Ett helt tal är delbart med
2, 	om sista siffran (entalet) är jämt eller 0.
3, 	om talets siffersumma är delbar med 3.
4, 	om det tal, som bildas av de två sista siffrorna är delbart med 4.
5, 	när sista siffran är 0 eller 5.
6, 	när villkoren för 2 och 3 både är uppfyllda.
7, 	när talets tiotal minus dubbla antalet av talets ental är delbart med 7.
           Ex.:392 är delbart med 7 (39-4=35)
8, 	när det tal, som bildas av de tre sista siffrorna är delbart med 8.
9, 	när talets siffersumma är delbar med 9.
10, 	när talets sista siffra är en nolla.

Denna lista kommer från denna sida

  • Matte Direkt sidan 41, magiska kvadrater.
  • Matte Direkt sidan 43, fattiga, rika och perfekta tal.

Lektion 11 - Repetition

se igeniom målen i arbetsplanen och repetera huvudräkning, multiplikation med uppställning, kort division etc.

prov

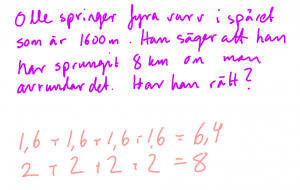
Tisdagen den 4 oktober.

Om du vill veta vad som gäller för proveet bör du läsa *arbetsplanen med målen för området.

Arbetsplanen innehåller desutom exempel inom varje mål. Ett bra snabbtest är att du kollar om du kan lösa dessa exempeluppgifter.

Övrigt

Projektarbete

  • Huvudräkning av Wiggo Kihlborn, är en powerpoint som jag har på hårddisken. jag skulle gärna publicera den om jag hade tillstånd men just nu har jag inte författarens kontaktuppgifter så jag kan inte ens fråga om han samtycker. Tills vidare finns boken Huvudräkning av författaren. jag tänker att eleverna kan få en huvudräkningsregel var att lära ut med exempel och förklaringar.

Bråk

Planer

Det finns tre beting för hur du kan planera ditt arbete för att göra betinget. En är på G-nivå, en är över G och en är super G.

Uppgifter

Se även Bråk år 7. Övningar, uppgifter, laborationer och Läsanvisningar ordnade efter delmål (i fet stil):

Kunna läsa och skriva bråk samt veta vad täljare och nämnare är

  • MatteDirekt Borgen 6A, sid 40-42.
  • Visa gärna första delen av denna PowerPoint om bråkens grunder men hoppa över den senare delan om förlängning och förkortning. Presentatione behöver på sikt förbättras, delas upp och byggas ut.
  • Övning. MattedDirekt 6A, Arbetsblad 2:9 som handlar om att slå tärningar. I korthet: Kasta två sexsidiga tärningar av olika färg. Den ena färgen visar täljaren och den andra nämnaren. Den spelare som får det största bråket vinner och får två poäng. Upprepa fem omgångar. Flest poäng vinner.

tal i bråkform och tal i blandad form.

  • MatteDirekt Borgen 6A, sid 43.

addition, subtraktion av bråk med samma nämnare.

  • MatteDirekt Borgen 6A, sid 44-45.

ange delen av något i bråkform.

  • MatteDirekt Borgen 6A, sid 46-47.

förkorta och förlänga bråk. (jämföra bråk)

Repetition och sammanfattning

  • En powerpoint med frågor om bråk i år 6. Eleverna svarar på frågor i punktform och ritar enkla bilder. Syftet är att öka begreppsförståelsen. den kan fungera som test efter att eleverna jobbat med webbmatte.se.

Tid över?

Övningar, uppgifter, laborationer och läsanvisningar ordnade efter delmål och synkade med boken MatteDirekt. Se även Bråk år 6.

Lektion 1 - inledning

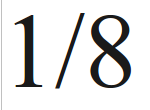
  • Inledande frågor sidan 75
  • Bokens mål sida 75

Uppgift. Matte Direkt sidorna 76-77.

Brak from Håkan Elderstig

  • PowerPoint om bråkens grunder samt om förlängning och förkortning. Filen kan laddas ned om man vill bygga ut powerointen. Den finns inbäddad till höger att titta på.

Lektion 2 - Delar av det hela

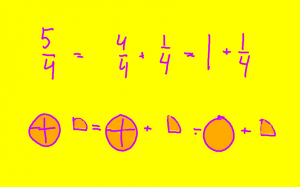
Film.

  • Täljare och nämnare, Kunskapshubben. OBS! man får ta filmen för vad den är. Den är lite fåning.
  • Blandad form, Kunskapshubben. Den här filmen är riktad till en viss grupp och därför är den personlig och skämtsam.

Beting. Matte Direkt sidorna 76-77.

Mål. ange delen av något i bråkform.

övningar

bråkövning
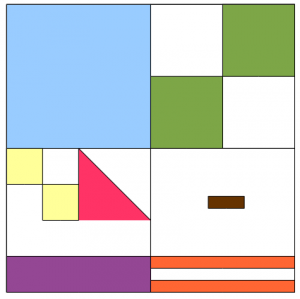
  • Övningsblad med grafiska bråk (pdf) En trevlig övning som antingen görs i datorn eller på papper som printas i färg och plastas in.

Datorövning.

Röd kurs. Delen och det hela på sidan 97

Geogebra

CC BY SA: Anthony Or. Education Bureau, Hong Kong. orchiming@gmail.com, http://www.geogebratube.org/material/show/id/14544

Lektion 3 - Vilket bråk är störst?

Den här lektionen handlar om att storleksordna bråk.

genomgång. Vi jämför bråken 3/4 med 4/5 samt 2/5 med 2/3.

Mål. Storleksordna naturliga tal och enkla tal i bråk- och decimalform.

Beting. Matte Direkt år 7 sidan 78.

Datorövning.

Röd kurs. bråk och proportioner sidan 99.

Lektion 4 - Bråk och decimaltal

Beting. Matte Direkt sidan 79.

Lektion 5 - Förlänga bråk - bråkplattor

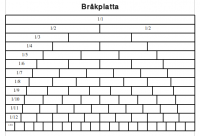
Bråkplatta
Bråkplatta

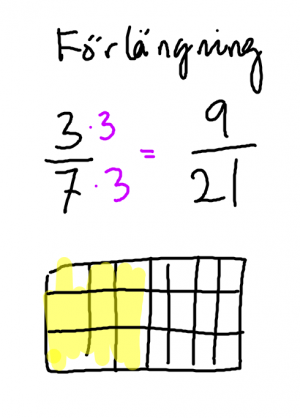
denna lektion handlar om att det finns flera bråk som uttrycker samma sak. 

Exempelvis 1/2 = 2/4.

Mål. förkorta och förlänga bråk. 

3/4 = 6/8 = 9/12

Genomgång. Visa bråkplattor. Här finns en wordfil med en bråkplatta som du kan skriva ut.

Den här filmen handlar om att omvandla bråk till decimaltal och vice versa. Men den kräver att man kan förlängning och förkortning av bråk.

Load video
YouTube

Beting. Matte Direkt sidorna 80-82

Klurig övning. Printa gärna dessa matematiska pyramider.

Datorövning. matteva - Förlänga och förkorta bråk

Överkurs: Wikipedia Junior på engelska

Röd kurs. Förlängning och förkortning sidan 100. Röd kurs. Delbarhet sidan 101.

Lektion 6 - Hur stor är delen?

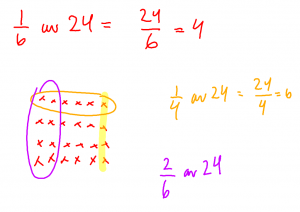
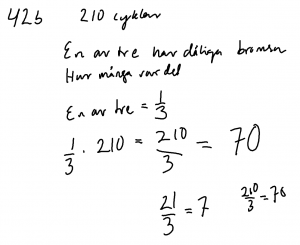
Idag handlar det om Bråk som andelen av ett atal. Deet svarar på frågan. Hur stor är delen?

Mål. Beräkna storleken utifrån given bråkdel. 

(ex 1/6 av 24).

Film. Hur stor är delen, Kunskapshubben.

Övning. Vi jobbar med Bråkplattoroch gör alla övningar som finns om man följer länken. De som är för år sex gör vi gemensamt.

  • Matte Direkt sidorna 82-83

Röd kurs. Delen och det hela på sidan 98

Lektion 7 - Addition och subtraktion med bråk

Bilden fr Wikimedia

I boken heter detta avsnitt Räkna med bråk.

Mål. Addition, subtraktion av bråk med samma nämnare.

Film.

Datorövning

Beting

  • Lös uppgifterna i Matte Direkt på sidan 84. Du bör nu ha räknat alla sidorna fram till denna.

Överkurs.

Ni som vill lära er mer kan titta på denna film som tar upp hur man adderar och subtraherar bråk med olika nämnare:

Load video
YouTube

Det kräver att man gör liknämningt genom att finna minsta gemensamma nämnaren.

  • Uppgift (Svår!): Vad blir summan 1/2+1/4+1/8+1/16+....... , där antalet bråk är oändligt.
Ledtrådarfinns här.
Uppgiften kan dels visa på problemet om man inte har samma nämnare med olika metoder att koma runt det och dels kanske hur man kan göra liknämnigt för att förstå problemet.

Röd kurs. Lägg samman och dra ifrånr sidan 97.

Lektion Extra - längd, vikt och volym - utgår 2010

Mål - Att räkna med vardagliga mått. 

Kunna utföra enhetsomvandling mellan längmått (km, m, dm, cm och mm)
Ex. hur många dm är 35,7 m, skriv 72,4 mm som cm
  • Matte Direkt sidorna 85-86.
  • MatteDirekt sid 87.

Laboration. Liter 

Tillverka ett litermått. Det får inte var 1 dm * 1 dm * 1 dm.

Material: Ris eller makaroner. Papper, tejp, linjaler, saxar.

Mål. Omvandlingar mellan tal i bråkform och tal i decimalform.

  • MatteDirekt sid 85-86 (med volymsmått och viktsmått).
  • Enheter för volym (1 sida i ppt) - om det är svårt med mått för volym.
  • MatteDirekt sid 102-103 (Röd kurs).

Lektion 8 - Räkna mer med bråk

Mål. Mmultiplikation av bråk med ett heltal.

  • Matte Direkt 87.
  • Även sant och falskat

Datorövning.

Röd kurs. sid 102-105. Bråk i decimalform, förlängning förkortning. Sammanfattning. Utmaning.

M Bondestam ger en förklaring som är överkurs för oss men kul ändå!

Load video
YouTube

Lektion 9 - Diagnosen - Repetition / utvikning

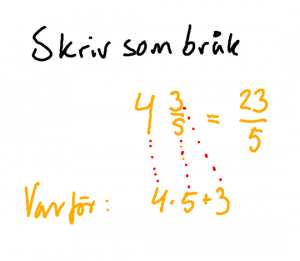
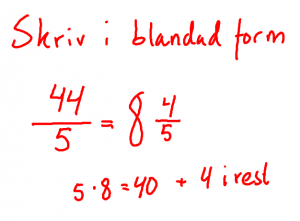
Diagnosen i boken

  • Matte Direkt sidorna 88-89.
  • Även Kluringarna

Dessa passar att printa ut:

Bra utmaning.

  • Repetitionsuppgifter från lärarhandledningen. Några lösningar till repetitionsuppgifterna finns här bredvid.

Extrauppgifter

  • Kluring. Hur många månader går det på ett hundår?
  • *MatteDirekt sid 88-89 (diagnos och kluringar)
  • Multiplikation med bråk. MatteDirekt år 8 sid 115
  • Division med bråk
  • Addition av bråk med olika nämnare. MatteDirekt år 8 sid 133. (kopia i pärm)
  • Skrivövningar om bråk
  • Tärningsspel med bråk. Det är inte riktigt spelbart men en intressant idé.
  • bråkfrågor i ppt Detta är en powerpointövning där eleverna sammanfattar kursen och tränar sig i att använda matematiska begrepp.
  • Övning. En variant av Arbetsblad 2:9 ovan. Giriggris med bråk. Tag en tiosidig tärning. Nämnaren bestäms i förväg till sex. Slå bråk med tiosidiga tärningen som täljare. Slå flera gånger och addera bråken. Om bråket blir större än ett förloras alla bråkpoäng i omgången. Om man stannar adderas bråken och skrivs upp. Gör vid behov om till hela och delar. Man kan byta täljare mellan omgångarna och även slå med sexsidig tärning för att bestämma nämnaren.
  • En powerpoint med frågor om bråk i år 6. Eleverna svarar på frågor i punktform och ritar enkla bilder. Syftet är att öka begreppsförståelsen. den kan fungera som test efter att eleverna jobbat med webbmatte.se. Finns även i år 6.

lektion X

Överkurs på år 9-nivå: Kunna beräkna hela mängden med hjälp av procentsats och delmängd.

  • Vattenmelonen
En vattenmelon med vikten 2 kg bestod till 99% av vatten. Efter att ha legat en hel dag i solen hade den minskat i vikt eftersom vatten avdunstat. Vattenhalten hade minskat till 98%. Hur mycket vägde melonen då?
Lösningar till vattenmelonen

Upptäck hur du kan använda en ekvation för att lösa svårare procentuppgifter

Om 18% av något är 4140, vad hade vi från början?
Redovisa först hur man kan tänka om man räknar ut vad e procent är osv.
Kalla priset från början för Y. Skriv en ekvation med Y, procentsatsen och 4140.
Försök generalisera ekvation genom att kalla procenttalet p osv.

Procent

här samlar jag all procent, dvs år 6, 7 och 8.

OBS Det är viktigt att man plockar sidnamnet från URL-fönstret så att det blir understreck istället för mellanslag i sidnamnet.

Planer

Beting

Delmål år 6

Förstå procentbegreppet. År 6

Behärska 100, 50, 25, 20, 10 % År 6

  • MatteDirekt 6B, sidorna 68-73.

Kunna göra enklare procentberäkningar i huvudet År 6

  • MatteDirekt 6B, sidorna 76-77.
  • Andra övningar.

Kunna beräkna hur mycket _____% är av något.

  • MatteDirekt 6B, sidorna 74-75.
  • Ett övningsblad från lektion.se, lektion-se_5742_Matteruta%.pdf på hårddisken min.
  • Kortis Hur många kronor billigare blir det om det är 10% rabatt på priset 200 kr?
  • Kortis Var handlar du billigast? A) 10 % rabatt på 150 kr eller B) 20 % på 170 kr.
  • Procentövningar på matteva

Speciella matteuppgifter till den som vill ha ett eget projekt

Mer än godkänt

Höjningar och sänkningar

  • MatteDirekt 6B (Röd kurs), sidorna 88-90.

Kunna utföra omvandlingar mellan tal i bråkform och tal i decimalform till procentform.

  • MatteDirekt 6B (Röd kurs), sidan 91.
  • Arbetsblad 8:7 i MatteDirekt 6B.
  • En uppgift som handlar om ekvivalensen mellan bråk, procent och decimaltal. Den lämpar sig för datasalen eller att elevern ritar om utskrifter av excelfilen
  • Här finns en interaktiv övning där mam ser bråk-, decimal- och procentform.

planer

Inledning

  • Läxor som vanligt men även en klurig hemuppgift som alternativ.

Lektion 1 - Introduktion Procent

Testa vad du kan redan

Ladda om sidan om du inte ser frågorna.

Det här testet bygger på en sida i Google Drive. När alla har gjort testet kan ni titta på statistiken och diskutera vad ni behöver öva på.

Svara på frågorna och tryck på Submit när du är klar.

Se resultatet genom att expandera rutan

Här ser vi resultatet. Vi kommer att projicera det på tavlan så vi kan diskutera det.

Det ser tyvärr ut som att jag måste vara inloggad för att se resultaten trots att jag har delat filen.

Här är kalkylarket där man kan nollställa resultatet genom att ta bort svarsraderna i tabellen.


Lär dig grunderna om procent

WEBBMATTE.SE Läs och begrunda - Välkommen till procent



Årstaskolan Stockholm - Kunskapshubben


Lektion 2 - procentbegreppet

MatteDirekt 7: sid 108-109.


Förstå procentbegreppet.

Teori: Vad är procent 1?

Procent betyder hundradelar. procent är att dela det hela i hundra delar. Här ser du att det egentligen är samma sak som bråk.

MatteDirekt 8:

  • Sid 142 bråk
  • Sid 143 Olika bråk men lika stor del
  • Sid 144 procent betyder hundradel
WEBBMATTE.SE Läs och begrunda - Presentation av begreppet


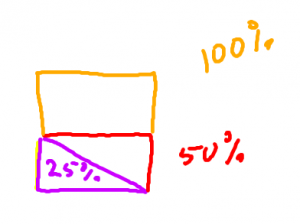
Lektion 3 - bråk-, decimal, procentform

MatteDirekt År 7: Röd kurs.  : Sidan 128.

MatteDirekt År 8:  : Sidan 145, jämför och använd procent

MatteDirekt 7: Uppgift: sid 110.

thmb
thmb

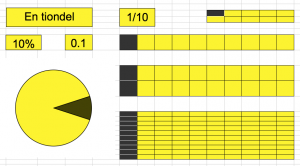
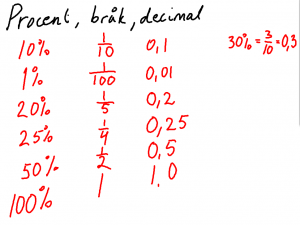
Mål: Kunna utföra omvandlingar mellan tal i bråkform och tal i decimalform till procentform.

Omvandlingar mellan bråk-, decimal- och procentform. Procent är bråk. Det vet vi sen tidigare. men hundradelar är decimaltal, 0.01. Så procent är även decimaltal

Data. matteva om procent-, decimal- och bråkform

Excel: Bilden med en tiondel i olika gulsvarta representationer kommer från en Excelfil som heter Procent_som_bilder.xlsx. Kanske vill du prova att skapa en egen bild av något annat procenttal.

lektion 4 - Enkla procenttal

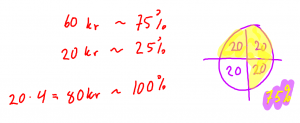
Mål: Behärska 100, 50, 25, 20, 10 %

Mål: kunna göra enklare procentberäkningar i huvudet

Teori: Räkna med procent 1

Utgå ifrån de kända procenttalen och deras motsvarigheter i bråkform. 

 exempel. 
 Om du vet att tio procent är en tiondel. 
 Då är 10% av 200 = 20. 
 Då vet du också att 30 % av 200 är 60 (3*20)

Samma sak med hundradelar
En procent av 350 är 3,50. 
4% av 350 är 4 * 3,50 = 14.

Teori: Räkna med procent 2

Tag procenten * det hela och dela med 100 

vad är 10 % av 400? 
400/100 = 4. 
10 * 4 = 40. 
Svar: 40.


Tänk! Tänk efter:

Exempel två ovan med hundradelar är ju både Räkna med procent 1 och 2!

'

Matte'Direkt År 7: Uppgift. sid 111.

MatteDirekt Röd kurs. : Sidan 129.

Film

Exempelvis lär vi oss att räkna ut 4 % av 120 i denna film: Martin Procent 1


Årstaskolan Stockholm - Kunskapshubben

Data. matteva har en övning med procentrutor som är ganska fiffig om man fastnar för den eller helt knäpp om man inte gillar den. Försök klura ut vad du tycker.


Uppgift 2: Gruppuppgift. Hälften och hälften igen. Arbetsblad 4:7 (Andelar i %) från Lärarhandledningen till matteDirekt år 7.

Lektion 5 - beräkna procent av något

Kunna beräkna hur mycket _____% är av något.

Webbmatte: Läs och begrunda Vi söker delen

Formel. Delen = Andelen * det hela

Uppgift.

MatteDirekt År 7: sid 112.

  • Gruppuppgift. Procentspel. Arbetsblad 4:8 från MD. Ett papper per elev så att ni kan läsa instruktionen men ni bör spela på samma plan. Lärarhandledning till Procentspel.

Lektion 6 - Räkna ut hur många procent det är

Mål. kunna beräkna procenttalet då delen och helheten är givna

Teori: Vad är procent 2?

Vad är procent om man ser till den praktiska användningen? 

Formel:  andelen = delen / det hela
WEBBMATTE.SE Läs och begrunda - Vi söker procenten


Bondestam återkommer med en formel för procenträkningen:

Load video
YouTube


Matte'Direkt år 7: Uppgift, sid 113.


MatteDirekt År 7: Röd kurs: Sid 130-131

Centikuber och procent

Centikuber och procent2 from Håkan Elderstig

Hur många procent är rosa? Laboration. Du får en näven centikuber av olika färg. Ta reda på hur många procent av dessa som är rosa. Om du inte har centikuber kan du be eleverna titta på denna flipchart.

Detta är en praktisk övning som börjar med en presentation. Sedan får du en näve centikuber i olika färger. uppgiften är att beräkan andelen rosa och ange detta som ett procenttal. Titta på presentationen först och testa sedan. Det är lätt!

Presentationen ligger inbäddad bredvid om man snabbt vill titta igenom den men eftersom den är animerad kan det vara roligare att köra powerpointfilen Centikuber och procent2.

Lärarhandledning

Gör en egen undersökning om procenten

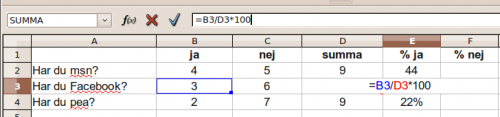
Resultatet av en undersökning om Facebookanvändande mm.
  • Gruppuppgift. Gör en undersökning där du ställer frågot till ett antal kompisar. Frågorna hittar du på själv. Det ska vara frågor som är av typen Ja/Nej eller där man kan svara rätt eller fel. Hitta på omkring tio frågor. frågorna kan gärna höra till ett tema, exemelvis sport , ordkunskap, matematik, film eller liknade. Sedan gör du en tabell i Excel och skriver in dina värden. Du kan låta Excel räkna ut procenten åt dig men det får din lärare visa dig. En exempelfil finns här.

Procent på E-nivå

Procent genomgang grunder2 from Håkan Elderstig

Här är en presentation av grunderna i procenträkning. Du får en genomgång av de olika sätten att tänka för att förstå procent. När du förstått detta kommer du förmodligen at använda dig av en formel för att räkna ut procentuppgifter. Mer om detta snart.

Det finns några saker som behöver en kommunikativ förbättring. I så fall ligger filen här: Powerpoint: Procent genomgång grunder2


Lektion 7 - Räkna mer med procent: decimaltal och multiplikation

Procent 2 varianter from Håkan Elderstig

Nu ska vi lära oss den metod som de flesta vuxna användernär de räknar procent i vardagliga livet. Det händer att elever säger "Varför sa du inte det här med en gång" när de får reda på detta. En didaktisk tankeställare för oss lärare.

Presentationen till höger finns för nedladdning här: Procent 2 varianter

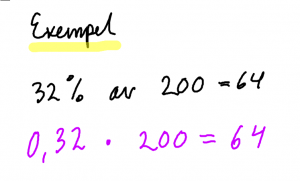
Mål: Kunna göra beräkningar med procent.

Teori: Räkna med procent 3

gör om procent till ett decimaltal. Multiplicera (gärna med miniräknare) 

32 % av 200 kr = 0,32 * 200 kr = 64 kr

Tillåt miniräknare på provet. Jag menar ... de kluriga uppgifterna är ju ändå svåra. de klurigaste uppgifterna är kanske att räkna procent 1...

Film

Här kommer först Mikael Bondestam och förklarar hur man räknar ut procent på de två vanligaste sätten, dels genom att multiplicera med ett decimaltal och dels genom att ta ett enklare procenttal.

Om frågan är vad 20 % av 50 kr är kan man dels ta 0,20 * 50 = 10 eller tänka 10 % innebär 50 / 10 = 5 kr och sedan ta 2 * 5 = 10 kr (vilket då är 20 %).

Vilket alternativ föredrar du?
Load video
YouTube

Mikael Bondestam om skillnaden mellan procent och procentenheter.

Load video
YouTube
WEBBMATTE.SE Läs och begrunda - Procentenheter och promille


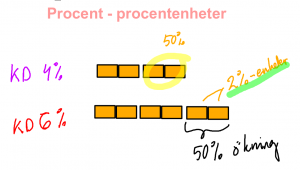
Övningsuppgift på procent - procentenheter

Det är skillnad på procent och procentenheter
Om vi tänker oss att miljöpartiet ökar från 8% till 10% i en undersökning av väljarsympatier då kan man uttrycka ökningen på två sätt.
1 Miljöpartiet har ökat med 2 procentenheter
2 Miljöpartiet har ökat med 25%
Fundera en stund och förklara hur det här hänger ihop.

MatteDirekt år 7: sid 114-116.

Röd kurs: Sid 132-135. mer än 100 %, prishöjning och sänkning, Procent på olika sätt.


Lektion 8 - Överkurs om procentformeln

Vi har ju tidigare stött på uttrycket andelen = delen / det hela. om man förstått och lärt sig det uttrycket har man stor nytta av att kunna modifiera algebraiska uttryck. Det finns några regler som gäller för vaad man kan göra för att förändra ett uttryck utan att förstöra sambandet. uttrycket om andel är egentligen tre uttryck i ett. Som det ser ut nu visar det hur man kan räkna ut andelen. men om man vrder på uttrycket kan man använda det för att räkna ut delen. Eller Det hela. tricket är att skriva om uttrycket så att rätt ord kommer för likhetstecknet.

Denna flipchart berättar hur man kan stuva om i formler och hur det används på andelen-formeln.

Vänd på uttrycket andelen = delen / det hela.

Då blir uttrycket: det hela = delen / andelen 

 exempel. Du vet att 4 motsvara 20 % Hur mycket är det hela? använd ekvationen 0,20 = 4 / x <==> x = 4 / 0,20

Jämför med det traditionella sättet att räkna enligt Räkna med procent 1. 

 Ex.:  Om 4 motsvarar 20 %
 så gäller att 2 motsvarar 10 %
 och då får vi att 20 motsvarar 100 %

Alternativ. Man ser kanske att 20 % är en femtedel. Då är det bara att multiplicera 4 med 5.

Det viktiga här är att inse att man kan göra på flera olika sätt men att de senare lämpar sig bäst för huvudräkning med enklare tal. Med siffror från verkliga uppgifter går det oftast inte jämnt ut och då lämpar sig ekvationslösningen och dator/miniräknare bäst.

Övning - Momsberäkningar

Du vet att det är 25% moms på en vara som man köper i affären men om du köper in saker i ett företag så anges priset ex moms (utan moms). Tänk dig att köpt en vara för 50 kr (ex moms). Hur mycket ska du lägga på för att få priset inkl moms?
Det är inte 25%, varför?

Kunskapskontroll med Google Forms

Klicka på länken och svara på frågorna. tryck Submit / Skicka när du är klar. Ladda om sidan ifall formuläret inte syns.

Det här testet kan eleverna göra och sedan kan man titta på statistiken över svaren och diskutera vad man behöver arbeta mer med i gruppen.

Se resultatet genom att expandera rutan

Här ser vi resultatet. Vi kommer att projicera det på tavlan så vi kan diskutera det.

Här är kalkylarket där man kan nollställa resultatet genom att ta bort svarsraderna i tabellen. Nollställ innan du kör detta med en ny elevgrupp.

Jag kan redigera frågorna här.--Håkan Elderstig 2 november 2012 kl. 23.06 (UTC)



Lektion 9 - Över G

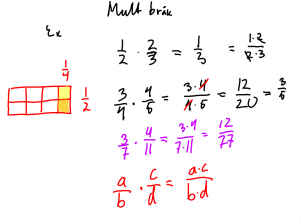
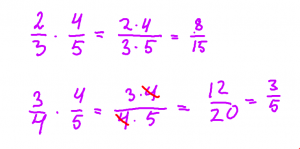
MD År 8

Det kan vara lämpligt att ta upp multiplikation av bråk sid 150, förändringsfaktor s 164, upprepade förändringar s 165, ekvationer s 166, division av bråk s 169-171.

Över G. Kunna räkna med förändring.

Över G: Kunna räkna med upprepad förändring.

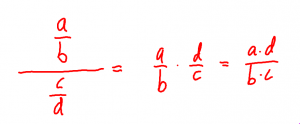
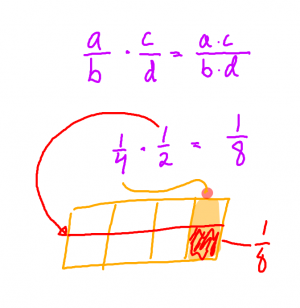
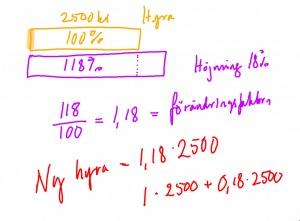
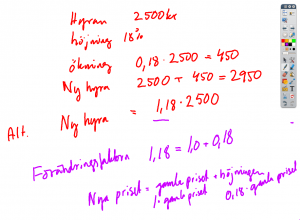
WEBBMATTE.SE Läs och begrunda - Förändring i procent


Procent på procent

Antag att vi har en vara som från början kostar 200 kr.
Priset på varan höjs fyra gånger med 5%.
Hur mycket kostar varan då?
Det handlar om en höjning i taget så det innebär inte en höjning med 4*5 = 20%.
Hur kan det se ut. Visa med ett exempel
Egentligen fungerar det lika dant oavsett vad ursprungspriset är. Kalla ursprungspriset för x och försök skapa ett uttryck för priset efter höjningarna.
Pröva att generalisera uttrycket ytterligare. Kalla räntan för r. hur ser uttrycket ut nu?

Lektion 10 - Över G2

Extrauppgifter på papper eller här:

Lektion 11 - repetition

Repetitionsuppgifter: Nu är det dags att dela ut repetitionsfrågor till kap 7 och 8. Dessutom kan det finnas gamla prov att öva på.

Om provet

Det är ok att använda miniräknare på provets B-del. Vi har bland annat lärt oss metoden att omvandla procent till decimalform och multoplicera med det hela. Detta fungerar i alla sammanhang och är anpassat för att använda miniräknare.

  • PPT Presentation med sammanfattning av grunderna i procenräkning.
  • Det finns en definition av procentbegreppet på svenska Wikipedia. Den är värd att läsa för att den är lite mer teoretisk än vad du finner i matteboken.
  • Jag kan rekommendera att en genomläsning av hela denna sida på wikiskola om procent.

Lektion 12 - Prov

lektion X

Överkurs på år 9-nivå: Kunna beräkna hela mängden med hjälp av procentsats och delmängd.

  • Vattenmelonen
En vattenmelon med vikten 2 kg bestod till 99% av vatten. Efter att ha legat en hel dag i solen hade den minskat i vikt eftersom vatten avdunstat. Vattenhalten hade minskat till 98%. Hur mycket vägde melonen då?
Lösningar till vattenmelonen

Upptäck hur du kan använda en ekvation för att lösa svårare procentuppgifter

Om 18% av något är 4140, vad hade vi från början?
Redovisa först hur man kan tänka om man räknar ut vad e procent är osv.
Kalla priset från början för Y. Skriv en ekvation med Y, procentsatsen och 4140.
Försök generalisera ekvation genom att kalla procenttalet p osv.

Geometri och mätningar

Planer

Övningar

Sidhänvisningar i boken och länkar till olika uppgifter.

Begreppen triangel, rektangel och kvadrat samt kunna rita dessa

Euklides. Bilden kommer från Wikipedia.
  • Allra enklaste geobrädesuppgifterna från och med åk 5

Räkna ut en figurs omkrets

  • MatteDirekt borgen 6A sid 68.

Räkna ut en sammansatt figurs omkrets

  • MatteDirekt borgen 6A sid 69.

Känna till några enheter för area

  • MatteDirekt borgen 6A sid 70-71.

Beräkna arean av en kvadrat

  • MatteDirekt borgen 6A sid 76-77.

Beräkna arean av en rektangel

Beräkna arean av en triangel

  • Finsk sida på nätet med en mängd matteuppgifter. Klicka på matematik och markera alternativen area, rektanglar och trianglar. Se till att cirklar mm inte är markerat. Sen är det bara att sätta igång och öva!
  • Övning med papper och sax. Tag ett papper och rita en så stor triangel som möjligt på papperet. klipp ut triangeln. Lägg de lossklippta bitarna på triangeln och se om de täcker den precis.
  • MatteDirekt borgen 6A sid 72-75.
  • Fler uppgifter för geobräden.
  • Rätta provet
  • Uppgift: Titta på denna sammanfattning i en bild. Den skulle kunna vara en kom-i-håglapp till geometrin. (Tack Sandra för hjälpen) Gör en egen kom-i-håglapp.

Extrauppgifter

  • MatteDirekt borgen 6A sid 78-79. (Diagnos och kluringar)
  • MatteDirekt borgen 6A sid 90-91. (Fyrhörningar)
  • Webbmatte om Geometri

Repetition

Beting

Varje lektion har ett beting som rymmer både G och Super G. Betinget är egentligen en lektionsplanering. Det betyder att betinget är uppdelat på varje lektion. Avsikten är att alla elever ska arbeta med samma saker på en lektion och att man ska kunna göra vettiga genomgångar och uppgifter för alla.

Diagnosen är valfri.

Allmänna övningar

Nu ska vi jobba mindre i boken och ha fler styrda övningar och genomgångar. Det kom vi överens om på Öppna huset.

Enheter och skala

Enhetsomvandlingar area

Vecka 6

Hastighet

Vecka 7

Skala

Vecka 8

De ska göra läxa 5 men de behöver inte lämna in den utan behåller boken för att göra läxa 6 efter lovet.

  • Måndag: Fortsätt räkna i boken från förra lektionen.
  • PPT En presentation om begreppen tid, hastighet, vikt och volym. Det blir lite repetition av det tidigare och samtidigt förberedelse för det kommande.

Volym

  • Tisdag: Vikt, sid 45-47. blå sid 57. Röd = valfritt. Fördjupningshäftet.
  • PPT Enheter för volym. Detta är endast en sida som sammanfattar övergångarna mellan olika voymsmått. Den kommer från presentationen ovan.
  • Torsdag: Volym 48-48. blå sid 58. Röd = valfritt. Fördjupningshäftet.

Extra

Vecka 10

Vecka 11

JMF gärna med arbetsplanen geometri år 6.

Lektion 1 - Intro

Proven. Dela ut proven. Klistra in proven i provhäftet.

nyheter. Nytt mot år sex är:

  • Vinklar
  • Att vi ska lära oss räkna ut cirkelns omkrets. Till detta använder vi pi.

Arbetsplan Titta på arbetsplanen.

Titta igenom inledningssidorna och diskutera frågorna där.

Bläddra igenom boken.

Anders lathund i Geometri år 7 Lathunden

Duggor. Vi kommer att ha två duggor. Se geometrisidan

Arbetstakt och beting. Det kommer att bli många korta genomgångar. Varje avsnitt i grön kurs får en genomgång. Dessutom skriver jag vilka uppgifter alla måste göra. Dessutom varvar jag detta med att ha genomgångar av innehållet i röd kurs. På dessa lektioner väljer du om du vill fortsätta med betinget från grön kurs på den tidigare lektionen eller om du vill göra rödkursuppgifter.

Geometrihistoria. Lernify

Lektion 2 - Vinklar

Genomgång läxa 3 uppgift 12. Hönsägg 55 gram. Strutsägg 2300 gram. Hur många många hönsägg motsvarar det?

Läxorna innehåller uppgifter som vi inte gått igenom. Det här är något som jag inte noterat förrän nu och förmodligen något som bokens författare också missat. Kanske är det en uppgift som hängt med sedan tidigare.

Uppgift 12 på läxa tre kräver division med tvåsiffrig nämnare och det har vi inte gått igenom och det finns inte heller förklarat i boken. Förr i tiden var det lättare med liggande stolen och liknande metoder men idag tycker vi (lärare) att eleverna kan göra detta i datorn eller med miniräknare.

Problemet är att hela kapitel 1 i boken är inriktat mot räkning utan miniräknare. De allra flesta uppgifterna förlorar sin mening om man använder miniräkanre. Uppgift nummer tolv på läxa tre har i och för sig en del av sin svårighet i att förstå uppgiften och välja räknesätt varför det kunde vara befogat att använda miniräknare men i så fall borde det stå i uppgiften.

Material. Vi behöver gradskivor.

Dema med gradskiva på tavlan.

Mål. Kunna uppskatta, mäta och beräkna vinklar, dvs

Beting. Alla ska göra alla uppgifterna på sid 46 i MD.

Lektion 3 - Vinklar igen

En spetsig vinkel
en trubbig vinkel

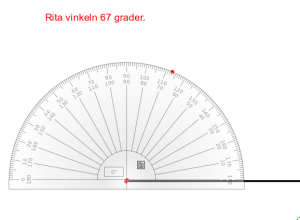
Mål

  • Kunna rita en viss vinkel.
  • Veta vad en spetsig, trubbig och rät vinkel är

Beting. Alla ska göra alla uppgifterna på sid 47 i MD och uppgift 6-7 på sidan 48.

Datorövning. matteva - uppskatta vinklar.

Lektion 4 - mer om vinklar (gärna två lektioner)

Vinkelsumma etc

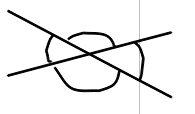
Det här hör till röd kurs. Du kan räkna fortsätta med dina uppgifter på grön kurs om du vill.

Beting över G. Röd kurs uppg 11-19.

Mål

  • Känna till förhållandet mellan vinklarna som uppstår då två linjer skär varandra

Begrepp

Namnge vinklar Matte Direkt sidan 66. 

Ex vinkeln BAC

Vertikalvinkel, sidovinkel och vinkelsumma. Matte Direkt sidan 67.

Bisektriser. Matte Direkt sidan 70.

Film. Fröken Matte om vinklar.

Eller denna:

Load video
YouTube

Båda filmerna är från kursen Matte A på gymnasiet men det går faktiskt att förstå ändå.

lektion 5 - Beskriva trianglar

Trianglar

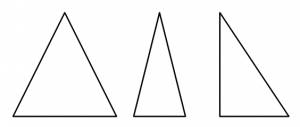
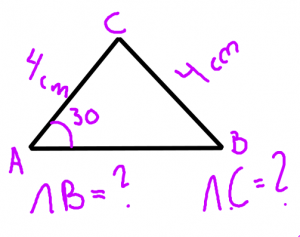
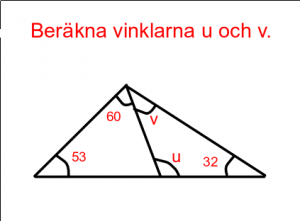
Mål

  • Veta att vinkelsumman i en triangel är 180 grader och kunna utföra beräkningar baserat på detta.
  • Kunna beskriva egenskaperna hos en spetsig, trubbig, liksidig, likbent och en rätvinklig triangel
Ex vilka sidor och vinklar som är lika
  • Veta skillnaden mellan rätvinklig, liksidig och likbent triangel.
Ex kunna beräkna alla vinklar i en likbent triangel om toppvinkeln är 30 grader.

Genomgång Vi löser vinkeluppgiften till höger tillsammans.

Film. http://www.arstaskolan.se/index.php?option=com_hwdvideoshare&task=viewvideo&Itemid=186&video_id=228 martin om olika typer av trianglar

Den här filmen visar hur man sätter namn på vinklar och sträckor. Sedan förklarar den vad likbenta och liksidiga trianglar har för egenskaper.

Load video
YouTube

Beting. Alla ska göra alla uppgifterna på sid 48-50 i MD. Det ska vara klart efter denna lektion. (sedan tidigare är man ju klar med alla uppgifter om vinklar på grön kurs)

Över G. Hur många olika trianglar kan man göra med samma omkrets (12 cm). Utmaning. Matte Direkt sidan 73. Detta är en bra uppgift. Gör den noga och redovisa så utförligt och snyggt du kan i datorn. Be om praktiskt material om diu behöver det.

Lektion 6 - Konstruera trianglar och bisektriser

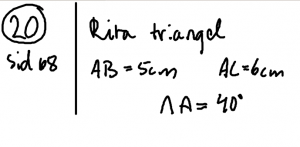
Mål. Kunna rita trianglar med hjälp av linjal, gradskiva och passare.

Mål. Kunna rita bisektriser med hjälp av linjal, gradskiva och passare.

Att göra. Fortsätt med betinget grön kurs om trianglar om du behöver det. Sid 48-50.

Överkurs. MatteDirekt sidorna 68-69 om att rita trianglar och sidan 70 om att konstruera bisektriser.

Lektion 7 - Beskriva rektangel och fyrhörningar.

En rektangel
Parallellogram

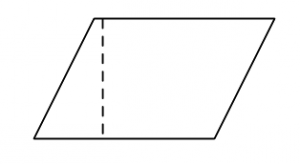
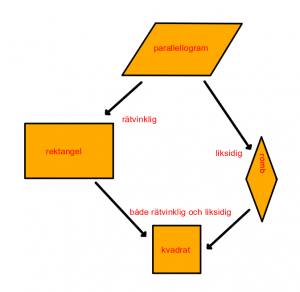
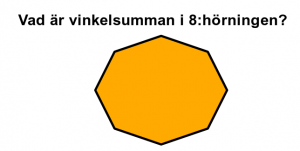
Begrepp: 

Parallellogram är en fyrhörnig geometrisk figur vars motstående sidor är parallella. 
Specialfall av parallellogrammer är kvadrater, rektanglar och romber.

En romb är en fyrhörnig geometrisk figur vars alla sidor är lika långa. 
Detta betyder också att motstående sidor är parallella.

En rektangel är en fyrhörnig geometrisk figur där alla fyra vinklarna är lika stora, d.v.s. räta (90°). 
Motstående sidor är lika stora.

En rektangel är ett specialfall av en parallellogram. 
En kvadrat är ett specialfall av en rektangel.

En kvadrat är ett specialfall av romb, rektangel och parallellogram.

All text om begreppen kommer från svenska Wikipedia.

Mål. Kunna beskriva en rektangel och en kvadrat samt kunna rita dessa.

Film. martin om olika fyrhörningar

Beting. Sidan 51 (grön kurs). Om du är klar med sidan gör du överkursuppgifterna nedan.

  • Geomeri åk 7 ppt. En presentation att använda vid genomgångar. Den skapades ursprungligen på ActivBoard.

Över G. Vinkelsumman i månghörningar. Matte Direkt sidan 71. Se kllippet nedan om vinkelsumman i en fyrhörning.

Load video
YouTube

Över G. Parallelltrapets.

Över G. Matteva - Sortera på symmetri.

Lektion 8 - Omkretsen för fyrhörningar, mm

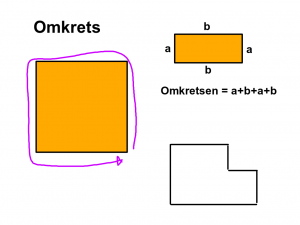
Genomgång.

  • Vad är omkrets?
  • Uppgift 28a

Provet kommer att vara vecka 47, må för 7B och torsdag för 7F

Michael bondestams film behandlar omkrets men även arean för en triangel. Det är repetition från förra året.

Load video
YouTube

Lektion 10 - Beskriv cirkeln och dess omkrets

Cirkelns radie och diameter


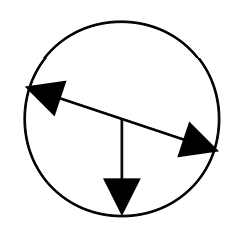
Mål.

  • Kunna beskriva en cirkel (sida, radie, diameter, mittpunkt)
  • Förstå vad talet Pi kommer ifrån och veta att det är en symbol för ca 3,14.

genomgång. vad är pi? genomgång - Cirkeln Cirklar och pi. En Powerpoint som beskriver nio olika övningar eller laborationer på pi. Svårighetgraden varierar från åk 6-9. Det finns ett exempel på hur två elever redovisar sitt arbete i ppt.

Mikael Bondestams film behandlar även arean. Det är överkurs :)

Load video
YouTube

Beting. Räkna alla uppgifter på sidan 53-54. Fördjupning. Matte Direkt sidan 64-65 där pi = 3,14.

Lektion 11 - Diagnosen

Nu kommer diagnosen sent i kursen och några av er har kanske gjort den redan men vi ska ändå göra den tillsammans. Alla på en gång. Och på tid. Därefter rättar du.

facit
facit

.

Efter det får ni reflektera över vad ni behöver öva på. Titta på diagnosresultatet. Bläddra igenom boken och titta på wikiskola. Därefter bloggar ni era instruktioner till er själva.

Lektion 12 - Repetition - Tänk till om geometri

Genomgång

  • Eleverna i en sjua gjorde varsin bild till en powerpoint som sammanfattar geometrin de jobbat med.
    • Eleverna gav synpunkter på varandras bilder och vi sammanställde det till en lagom lång presentation. Dessutom innehåller den en förbättringsuppgift för kommande elever. Eleverna berättar också vad de tyckte om övningen.
  • QWiki
  • Powerpointfrågor - geometri.En ppt med frågor till eleverna. Den tränar begrepp och förståelse. Eleverna kan jobba en och en eller två och två och skriver sina svar i ppt-filen. Filemn kan de spara på en server och få rättad.
  • Repetitionsuppgifter från lärarhandledningen som delas ut på papper.

Extrauppgifter

Anders lathund i Geometri år 7 Lathunden

Lektion 13 - Formelsamling /sammanfattnig

  1. Eleverna gör en formelsamling i ppt.
  2. Jag ställer frågor och de svarar.
  3. Sedan gensvar och hoplänkning.
  4. Vi tittar igenom den tillsammans och gör förbättringar.

Laboration – Omkrets delat med diameter

Inledning Börja med några mätningar. Ungefär hur lång omkrets har en cirkel med diametern. Försök att rita upp cirklarna och lägg ett snöre eller måttband runt. 

a)10 cm   b) 7 dm  c)2 m

Fortsättning Eleverna mäter omkrets och diameter på olika objekt

  • De gör en tabell
  • De dividerar ..
  • De drar slutsatser

Genomgång av geometriprovet

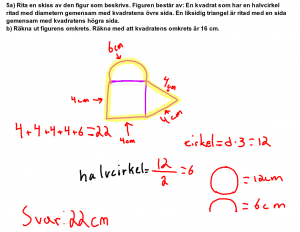
uppg 5 på geometriprovet

{{}}

Algebra

Statistik

Sannolikhetslära

Hämtad från ”https://wikiskola.se/index.php?title=Testsida&oldid=9017”