Algebra 2C
Intro Algebra Ma2C
Förenkling av uttryck
Ekvationer Ma2C
Kvadrerings- och konjugatregler
Parentesmultiplikation
Kvadreringsregeln Ma2C
En första läxa
Det är viktigt att vi kommer igång med att lära oss Geogebra.
Första naturliga ingången är egentligen räta linjen där det blir en tydlig koppling mellan funktion och utseende.
GGB-uppgift 1
Ladda ner programmet.
Skriv in en valfri räta linjens funktion.
Ändra färg och tjocklek på grafen.
Ändra så att grafens egenskap syns.
Mejla filen till din lärare.
Konjugatregeln Ma2C
Ekvationer med x^2-term
Andragradsekvationer
Enkla andragradsekvationer
Fullständiga andragradsekvationer
Kvadratkomplettering
Diagnos 2 med pq-formeln
Andragradsekvationer och rötter
Komplexa tal
Teori
| Definition |
|---|
| Komplexa tal
Ett komplext tal består av en realdel [math]\displaystyle{ a }[/math] och en imaginärdel [math]\displaystyle{ b }[/math].
|
Läs mer: Komplexa tal på wikipedia
Vad ska man ha komplexa tal till?
- Komplexa tal används när man räknar på växelström.
- Titta på denna ppt från Uppsala.
- j-omegametoden
Komplexa rötter
x2 = -16 har ingen reell rot men däremot två komplexa. Det beror på att lösningen är roten ut ett negativt tal. Roten ur -16 är +4i respektive -4i.
x2+3x+16=0 har också två komplexa rötter fast här beror varje rot av både en realdel och en imaginärdel.
Rotekvationer
Teori
Rotekvationer innehåller x-termer och roten ur x-termer. Man löser dem genom att kvadrera båda leden.
- [math]\displaystyle{ \sqrt{x+2} = x }[/math]
Kvadrera båda sidorna:
- [math]\displaystyle{ x+2 = x^2 }[/math]
- [math]\displaystyle{ x^2 - x - 2 = 0 }[/math]
- [math]\displaystyle{ x = \frac{1}{2} \pm \sqrt{\frac{1}{4} + 2} }[/math]
- [math]\displaystyle{ x = \frac{1}{2} \pm \sqrt{\frac{1}{4} + \frac{8}{4}} }[/math]
- [math]\displaystyle{ x = \frac{1}{2} \pm \sqrt{\frac{9}{4}} }[/math]
- [math]\displaystyle{ x = \frac{1}{2} \pm \frac{3}{2} }[/math]
- [math]\displaystyle{ x_1 = - 1, x_2 = 2 }[/math]
Viktigt att kolla om man har falska rötter.
[math]\displaystyle{ -1 }[/math] är en falsk rot eftersom den inte gör att vänster led och höger led blir lika i ursprungsekvationen.
Svaret är alltså [math]\displaystyle{ x = 2 }[/math]
Problemlösning med ekvationer
Professionell matte
Har ni tänkt på att det är ett tag sedan vi gjorde matte som man har nytta av i vardagen? Kvadreingsregeln, konjugatregeln, kvadratkompletteringen och pq-formel hör inte till vardagsmatten. De hör till den professionella matten. Sådan matte som ingenjörer använder.
Vad ska man ha andragradsekvationer till?
De används i spel till exempel.
- Wikipedia om projectile motion
- Här finns länkar om fysikmotorn bakom Angry Birds och mycket annat
- Det finns ett exempel med två bollar som faller och där den ena även far i x-led. Banan beskriver en parabel och det är ett klassiskt exempel på en andragradsekvation. Du kan se Action Script-koden.
PhET
En idé kan vara att ta en screenshot på en projektilbana från PhET-simuleringen ovan och klistra in i GeoGebra. Sedan sätter man tre eller fler punkter på kurvan och anpassar till en andragradsekvation. Det visar om inte annat bakvägen att fysiken innehåller andragradsfunktioner. Om man är osäker på hur man anpassar punkter till en funktion så har jag gjort det med mätvärdena från laborationen på tyngdacceleration.
Ekvationslösning med faktorisering
Diagnosen blir läxa att göra om hemma och denna gång ska den ha alla rätt. Det gäller alla. Facit kommer upp på tisdag så kan alla rätta själva.
På tisdag som är en lång lektion kommer vi att göra uppdelning i faktorer både med konjugatregeln och kvadreringsreglerna om det går.
Uppdelning i faktorer med konjugatregeln
| Uppgift |
|---|
|
Först ska vi repetera konjugatregeln med ett lösblad där det är rad snabba uppgifter. Dessa uppgifter bör klaras av på mindre än tre minuter. |
Uppdelning i faktorer med kvadreringsreglerna
| Uppgift |
|---|
|
Här ska vi också repetera kvadreringsreglerna med ett lösblad. |
Faktorisering och ekvationer
Onsdag
Repetera lösbladet från förra lektionen en gång till. I övrigt struntar vi i beting på faktorisering med kvadreringsregelerna.
Dagens beting: 1426-1430
Dataövning - konsekutiva tal
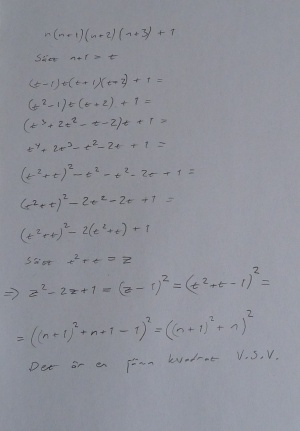
Del ett (n-1)(n+1)+1
Del två
Del tv är svårare. Det handlar om fyra konsekutiva tal. Addera ett till produkten av de fyra talen och ta roten ur. Detta ska bli ett heltal.
- Wolfram|Alpha har en lösning men ingen förklaring.
- Med hjälp av den ledtråden från Wolfram ser min lösning ut så här.
- Tanja löser uppgiften genom att pröva.
- Fredrik använder kvadratkomplettering och substitution för att lösa uppgiften. Lösningen syns i bilden till höger.
- Charlie i NV11 löser det genom att hitta mönster i de tal han prövar med och ...
Prov onsdag vecka 6
| Uppgift |
|---|
| Diagnos 14 |
Repetition på fredag och måndag
Uppgift: Khan Academy
Uppgifter
- Läs sammanfattningen på sidan 54.
- Gör Test 1 på sidan 55.
pappersövningar
- Öva ekvationer (= Extrablad ekvationer): finns bara på papper
- Faktorisering: finns bara på papper
- Öva enkla andragradsekvationer: finns bara på papper
Provet skall vara tisdag vecka 7 (ligger på SchoolSoft).
Facit och bedömning
Christers bedömningsmall från mellandagen bör finnas här. Lösningen är till Prov 1 ver 4 (2013)


