Lägesmått och spridningsmått: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) |
||
| Rad 91: | Rad 91: | ||
{{matteboken |[https xxx] }}<br /> | {{matteboken |[https xxx] }}<br /> | ||
|} | |} | ||
{{clear}} | |||
== Exit ticket == | == Exit ticket == | ||
Versionen från 1 maj 2018 kl. 10.10
Teori
Exempeluppgift - medelvärde
Varationsbredd och låddiagram
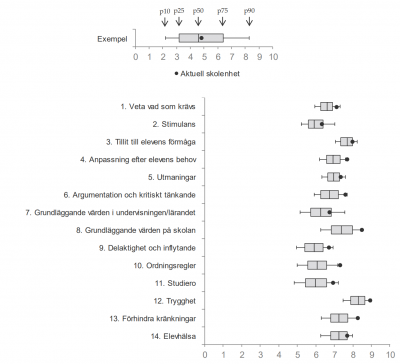
Några spridningsmått Sidorna 217-221.
Medelvärde och standardavvikelse
Här kan man tänka sig att eleverna gör egna undersökningar och redovisar...
| Definition |
|---|
Medelvärde, variationsbredd och standardavvikelse
|
Standardavvikelse
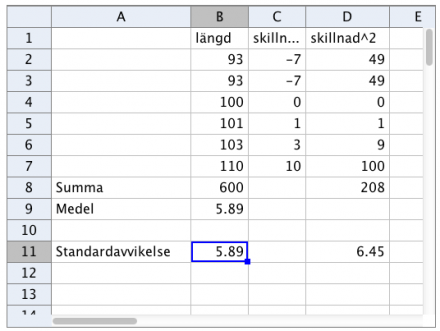
Så här kan det se ut i Geogebra om du beräknar standardavvikelsen själv. Till höger är bara en bild. Om du vill se GGB-filen klickar du på länken nedan.
Här är ett exempel där man använder Geogebras funktion för att beräkna standrdavikelsen:
| Uppgift |
|---|
| När började polarisarna smälta
Följ länken till Arctic Sea Ice News & Analysis Undersök vilket år isens areae hamnade utanför två standardavvikelser från medelvärdet under åren 1979-2000.
|
Aktivitet
Undersök statistikfunktionen i Python
Här är några enkla statisktikfunktioenr som finns i Python.
Statistikbibliotek i Python
Det finns ett bibliotek med fler statistikfunktioner.
Medelvärde med listor i Python
Lär mer
|
|




