Lägesmått och spridningsmått: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
(Skapade sidan med '{| |- | {{malruta | xxx Här undersöker vi xxx. }} | | {{sway | [https xxx]}}<br /> {{gleerups| [https xxx] }}<br /> {{matteboken |[https://www.matteboken.se/lektioner/matt...')
 
Rad 16: Rad 16:
<pdf>Medelvarde-08052012125522.pdf</pdf>
<pdf>Medelvarde-08052012125522.pdf</pdf>


{{clear}}


=== Varationsbredd och låddiagram ===
[[Fil:Skolinspektionen anv lådagram.PNG|400px|höger]]
'''Några spridningsmått''' Sidorna 217-221.
{{svwp|Lådagram}}
{{clear}}
=== Medelvärde och standardavvikelse ===
Här kan man tänka sig att eleverna gör egna undersökningar och redovisar...
{{defruta |'''Medelvärde, variationsbredd och standardavvikelse'''
: Aritmetiskt '''medelvärde''': <math>\, M(x) =\mu = \frac{x_1 + x_2 + \cdots + x_n}{n} = \frac{1}{n}\sum_{i=1}^n x_i</math>
: '''Variationsbredd''' är inom statistik ett mått på skillnaden mellan det minsta och största värdet i ett givet material. Variationsbredden räknas ut genom att ta skillnaden mellan max- och min-värdet i en datatabell.<br />
: '''Standardavvikelse''' kan skrivas:
:<math>\sigma = \frac{1}{n} \sqrt{\sum_{i=1}^n (x_i - \mu)^2};\qquad</math>
}}
=== Standardavvikelse ===
[[Fil:Standardavvikels_i_Geogebra.png|440px|right]]
Så här kan det se ut i Geogebra om du beräknar standardavvikelsen själv. Till höger är bara en bild. Om du vill se GGB-filen klickar du på länken nedan.
{{GGB|[[Standardavvikelse - uppgift i Geogebra]] }}
Här är ett exempel där man använder Geogebras funktion för  att beräkna standrdavikelsen:
{{GGB | '''Medelvärde och standardavvikelse'''
[https://www.geogebratube.org/student/m10956 Exempel på stapeldiagram.]
}}
{{uppgruta  | '''<big>När började polarisarna smälta</big>'''
Följ länken till [http://nsidc.org/arcticseaicenews/charctic-interactive-sea-ice-graph/ Arctic Sea Ice News & Analysis]
Undersök vilket år isens areae hamnade utanför två standardavvikelser från medelvärdet under åren 1979-2000.
}}
{{clear}}
== Aktivitet ==
=== Python 1 ===
{{Python|[[Statistikfunktionen_i_Python]] }}
Det finns ett bibliotek med fler statistikfunktioner.
{{clear}}
=== Undersök statistikfunktionen i Python ===
{{Python|[[Statistik_i_python]] och [https://wikiskola.se/index.php?title{{=}}Kategori:Python Fler uppgifter] }}
Här är några enkla statisktikfunktioenr som finns i Python.
{{clear}}
{{clear}}


Versionen från 27 april 2018 kl. 12.23

Mål för undervisningen xxx

Här undersöker vi xxx.

Swayen till detta avsnitt: [https xxx]


läromedel: [https xxx]


Läs om Lägesmått


Teori

Exempeluppgift - medelvärde


Varationsbredd och låddiagram

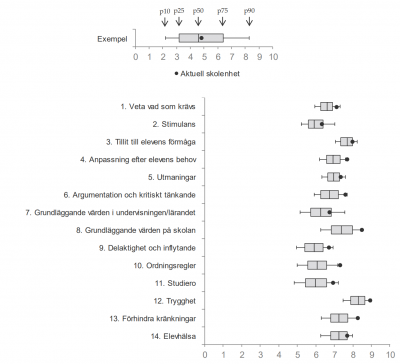
Några spridningsmått Sidorna 217-221.

Wikipedia skriver om Lådagram

Medelvärde och standardavvikelse

Här kan man tänka sig att eleverna gör egna undersökningar och redovisar...

Definition
Medelvärde, variationsbredd och standardavvikelse
Aritmetiskt medelvärde: [math]\displaystyle{ \, M(x) =\mu = \frac{x_1 + x_2 + \cdots + x_n}{n} = \frac{1}{n}\sum_{i=1}^n x_i }[/math]


Variationsbredd är inom statistik ett mått på skillnaden mellan det minsta och största värdet i ett givet material. Variationsbredden räknas ut genom att ta skillnaden mellan max- och min-värdet i en datatabell.


Standardavvikelse kan skrivas:
[math]\displaystyle{ \sigma = \frac{1}{n} \sqrt{\sum_{i=1}^n (x_i - \mu)^2};\qquad }[/math]


Standardavvikelse

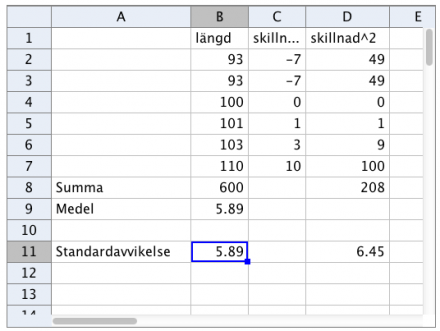
Så här kan det se ut i Geogebra om du beräknar standardavvikelsen själv. Till höger är bara en bild. Om du vill se GGB-filen klickar du på länken nedan.

Geogebra Undersök med Geogebra-applet: Standardavvikelse - uppgift i Geogebra


Här är ett exempel där man använder Geogebras funktion för att beräkna standrdavikelsen:

Geogebra Undersök med Geogebra-applet: Medelvärde och standardavvikelse

Exempel på stapeldiagram.


Uppgift
När började polarisarna smälta

Följ länken till Arctic Sea Ice News & Analysis

Undersök vilket år isens areae hamnade utanför två standardavvikelser från medelvärdet under åren 1979-2000.



Aktivitet

Python 1

Programmeringsuppgift

Statistikfunktionen_i_Python

Det finns ett bibliotek med fler statistikfunktioner.


Undersök statistikfunktionen i Python

Programmeringsuppgift

Statistik_i_python och Fler uppgifter

Här är några enkla statisktikfunktioenr som finns i Python.

Aktivitet

Medelvärde med listor i Python

Programmeringsuppgift

Medelvärde_med_listor_i_Python

Uppgift

Uppgift
xxx



Lär mer

Exit ticket

Hämtad från ”https://wikiskola.se/index.php?title=Lägesmått_och_spridningsmått&oldid=46713”