Lägesmått och spridningsmått

Teori

Varationsbredd och låddiagram

Figure 2. Boxplot with whiskers from minimum to maximum

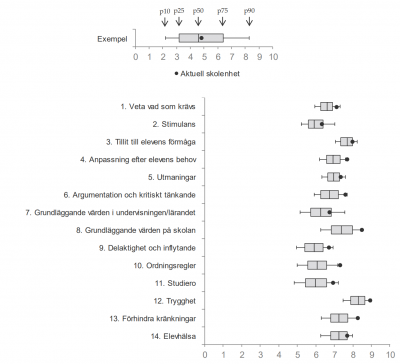
Definition

Låddiagram Lådagram, låddiagram eller boxplot är ett diagram där ett statistiskt material åskådliggörs i form av en låda, som rymmer den mittersta hälften av materialet. Lådagrammet sammanfattar materialet med hjälp av fem värden: medianvärdet, undre och övre kvartilen samt minimum och maximum. Eventuella extremvärden betraktas som utliggare och markeras med egna symboler. Wikipedia skriver om Lådagram

Låddiagram är inte så vanligt förekommande i nyhetsprogram och tidningar men dyker ofta upp på prov i Ma2c.

Medelvärde och standardavvikelse

Här kan man tänka sig att eleverna gör egna undersökningar och redovisar...

Definition

Medelvärde, variationsbredd och standardavvikelse Aritmetiskt medelvärde: [math]\displaystyle{ \, M(x) =\mu = \frac{x_1 + x_2 + \cdots + x_n}{n} = \frac{1}{n}\sum_{i=1}^n x_i }[/math] Variationsbredd är inom statistik ett mått på skillnaden mellan det minsta och största värdet i ett givet material. Variationsbredden räknas ut genom att ta skillnaden mellan max- och min-värdet i en datatabell. Standardavvikelse för ett stickprov kan skrivas: [math]\displaystyle{ s = \frac{1}{n-1} \sqrt{\sum_{i=1}^n (x_i - \mu)^2};\qquad }[/math]

Standardavvikelse i GeoGebra

Kör GeoGebra i Gafikmod.

Skapa listan genom att skriva in exempelvis {1,3,2,4,11,12}. GeoGebra kommer att döpa din lista till Lista₁.

Nu kan du skriva standardavvikelse och GeoGebra kommer att ge dig olika förslag. Välj till exempel standardavvikelse för urval och Skriv in Lista₁ (här får du använda under score).

Polarisen

Uppgift
När började polarisarna smälta Följ länken till Arctic Sea Ice News & Analysis Undersök vilket år isens areae hamnade utanför två standardavvikelser från medelvärdet under åren 1979-2000.

Aktivitet

Undersök statistikfunktionen i Python

Här är några enkla statisktikfunktioenr som finns i Python.

Statistikbibliotek i Python

Det finns ett bibliotek med fler statistikfunktioner.

Lär mer

Testa standardavvikelse i GeoGebra Classic

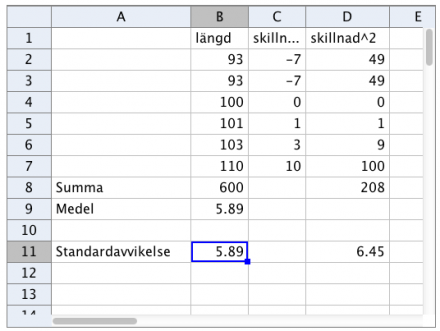
Så här kan det se ut i Geogebra om du beräknar standardavvikelsen själv. Till höger är bara en bild. Om du vill se GGB-filen klickar du på länken nedan.

Här är ett exempel där man använder Geogebras funktion för att beräkna standrdavikelsen: