|
|
| (97 mellanliggande sidversioner av 3 användare visas inte) |
| Rad 1: |
Rad 1: |
| == Lektion 1 Geometriskt bevis == | | == 2.1 Repetition == |
| {{lm3c|aktiviteten|57}}
| |
|
| |
|
| {{uppgruta|Ni ska göra en ppt och förklara de fyra geometriska bevisen. Det kommer att vara CC och ni jobbar gruppvis två och tvås eller tre. Det kommer att publiceras. Ni börjar alla på papper och sedan gör ni ett som vi kommer överens om i presentationen. För att lyckas kan ni behöva läsa sidan 54 i boken eller gå tillbaks till Ma2C länk...
| | == [[Lektion 1 Geometriskt bevis]] == |
|
| |
|
| Exempel på förklarande ppt: [[Algebra_2C#Parentesmultiplikation|Multiplikation genom uppdelning av talen]]
| | Bokens introduktion till kapitlet. |
|
| |
|
| Här ska ni jobba alla tillsammans på en presentation i Google Drive.
| | == [[Lektion 2 - Repetition potenser]] == |
|
| |
|
| [https://docs.google.com/presentation/d/1Uax4wMd-3sc6Cw0jmgdePtqMLoFm5MwcDA5eKKxlRk4/edit Klicka och börja jobba här] | | == [[Lektion 3 - Kvadreringsreglerna och andragradsekvationen]] == |
|
| |
|
| Presentationen är för tillfälet stängd för redigering för att undvika klotter. --[[Användare:Hakan|Håkan Elderstig]] 21 oktober 2012 kl. 12.25 (UTC)
| | == [[Lektion 4 - Faktorisera]] == |
| }}<html>
| |
| <iframe src="https://docs.google.com/presentation/embed?id=1Uax4wMd-3sc6Cw0jmgdePtqMLoFm5MwcDA5eKKxlRk4&start=false&loop=false&delayms=5000" frameborder="0" width="480" height="389" align="left" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true"></iframe>
| |
| </html>
| |
|
| |
|
| '''Resultatet''' ser du här till vänster.
| | == [[Lektion 5 - Aktivitet Geometriska bevis]] == |
| {{clear}}'
| |
| {{flipp|''Gå till elktion 2 och 'titta igenom provet igen'''}}
| |
| {{clear}}'
| |
|
| |
|
| == Repetition -Algebra == | | == 2.2 Polynom och faktorer == |
|
| |
|
| ''Här kan du repetera kvadreringsreglerna genom at expandera fönstret nedan:''
| | == [[Lektion 6 - Polynom, faktorer]] == |
| {{transclude|{{:kvadreringsregeln}}}}
| |
| ''Här kan du repetera konjugatregeln genom at expandera fönstret nedan:''
| |
| {{transclude|{{:konjugatregeln}}}}
| |
|
| |
|
| == Lektion 2 - Repetition potenser == | | == [[Lektion 7 - Faktorer, rötter och nollställen]] == |
|
| |
|
| Repetera avsnittet om potenser genom att expandera avsnittet nedan.
| | == 2.3 Rationella uttryck == |
|
| |
|
| {{lm3c|Sedan gör du uppgifterna i boken, sid 53-54.}}{{clear}}
| | == [[Lektion 8 - Förkorta rationella uttryck]] == |
|
| |
|
| ''Här kan du repetera potensreglerna genom at expandera fönstret nedan:''
| | == [[Lektion 9 - Mer om förenkling]] == |
|
| |
|
| {{transclude|{{:potenser}}}}
| | == Lektion 10 - [[Multiplikation och division av rationella uttryck]] == |
|
| |
|
| == Polynom, faktorer, rötter och nollställen == | | == Lektion 11 - [[Addition och subtraktion av rationella uttryck]] == |
|
| |
|
| {{lm3c|Här kan ni behöva repetera sidorna 56-65}}{{clear}}
| | == 2.4 Ekvationer och olikheter == |
| * Om andragradspolynomet p(x) har nollställen x=a och x=b kan vi faktorisera polynomet till p(x) = k*(x-a)*(x-b) där k är koefficienten framför x^2-termen
| |
| * Om ett andragradspolynom saknar nollställen, kan det inte faktoriseras!
| |
| * Om ett andragradspolynom har ett enda nollställe, t.ex. dubbelroten x=a kan polynomet skrivas på formen p(x) = k*(x-a)*(x-a) = k*(x-a)^2
| |
| <br />
| |
|
| |
|
| '''Hoppa över till senare:''' Det här är reptetion av tidigare stoff. Boken har en logisk sekvensiell uppbyggnad vilket kan bli tråkigt i längden. Ett alternativ är att gå rakt på de centrala delarna.En intressant möjlighet är att hitta en annan ingång till det nya centrala stoffet och istället repetera detta när behovet och motivationen finns.
| | Sid 79-89. |
|
| |
|
| === Repetition från tidigare kurser ===
| | ''Kursivt då ej centralt innehåll.'' |
|
| |
|
| * [[Taluppfattning_och_Aritmetik#Lektion_6_-_Potenser|Ma1C - Potenser]]
| | ==Lektion 12 - [[Ekvationer med nämnare]] == |
|
| |
|
| == Rationella uttryck == | | == Lektion 13 - [[Absolutbelopp]] == |
| {{lm3c|Rationella uttryck|66-78}}
| |
|
| |
|
| === Syfte === | | == Bevisa Pythagoras sats == |
|
| |
|
| Vi ska bli nyfikna på rationella uttryck genom att undersöka hur de ser ut. Genom att beskriva dem övar vi språket. Detta ska sedan leda till en planering av vad och hur vi ska lära kommande lektioner.
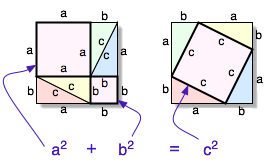
| | [[Fil:Pythagorean proof.png|miniatyr | right]] |
|
| |
|
| === Arbetsformer ===
| | Till höger ser du ett geometriskt bevis av Pythagoras sats. |
|
| |
|
| Para ihop er med en elev från varje klass i grupper om två, så att det finns minst en dator i gruppen.
| | Frågan är - kan du bevisa den algeriskt? |
|
| |
|
| Här finns [http://www.geogebra.org/cms/en/download GeoGebra att ladda ner]. Kicka på Webstart.
| | {{clear}} |
|
| |
|
| {{uppgruta|
| | == En övning i att ta fram provfrågor! == |
| Testa ditt uttryck i GeoGebra. Fundera över varför grafen ser ut som den gör.
| |
|
| |
|
| Beskriv grafen som bildas i GeoGebra med vanliga ord.
| | {{print|[[Media:Inför_prov_Ma3c,_Beskrivning_av_typuppgifter.pdf|beskrivning av typuppgifter]] som underlag för att göra provfrågor och facit}} |
| * Varför ser den ut så?
| |
| * Kommer grafen att skära y-axeln?
| |
| * Kommer grafen att tangera y-axeln?
| |
| * Kan x anta alla olika värden?
| |
| * Motivera dina svar.
| |
| * Försök hitta ett matematikord som är användbart. Ett tips är att titta lite i boken.
| |
|
| |
|
| '''Redovisa''': Skriv in din funktion och beskrivning här: [https://docs.google.com/document/d/1by0ILAzPXUEtdGZiPWRIc5k4UHyQq9eXzXUwJMWOWLY/edit Redovisa på Google]
| | Ni skapar en egen gemensam diagnos: |
| }} | | <br />I detta google-dokument kan ni skapa era uppgifter: [https://docs.google.com/document/d/1XHvoOU061d_Uo39CHCMkgNgdsGvWJEu90K77grod8xc/edit provfrågor] {{print|[[media:Inför_provet%2C_exempeluppgifter-2.pdf|Provfrågorna]]}} |
| | | <br />I detta google-dokument kan ni lägga lösningar till uppgifterna: [https://docs.google.com/document/d/19Ceh-bUUyRdtSRiTm09Ar0VuT23HOZUeHvcXrxfOH2E/edit Facit till provfrågorna] {{print|[[media:Inför_provet,_facit.pdf|Facit]]}} |
| === Mer ===
| | <br /><br /> |
| | | Här lägger vi upp de färdiga uppgifterna och lösningarna onsdag 5 december som ni får öva på till lektionen på torsdag 6 december. |
| Andra exempel att prova i GeoGebra:
| | <br />Vi tittar sedan på lektionen vilka uppgifter som ni tycker är svårast och löser några tillsammans. |
| :: f(x)=3/x
| | <br /><br /> |
| :: h(x) = 0.1 / (x - 1)
| | Utifrån era exempeluppgifter skapas ett prov med liknande uppgifter. Provet är på fredag 7 december. |
| :: g(x) = 1/x^2
| | <br />Ni får sedan rätta varandras prov. |
| :: f(x)= (2x^2+3x)/(x-4)
| | <br />Efter det berättar ni vad vi behöver öva mer på i grupp |
| :: f(x) = sin(x) / x
| | <br /> ytterligare några exempeluppgifter kommer under torsdag |
| | <br /><br /> |
| | Ni gör även individuella studieplaner för nästa vecka. |
| | <br />Sedan kommer vi att börja på nästa kapitel - Derivator. Vid behov kan vi återkomma till detta kapitel. |
|
| |
|
| * Beter sig denna kurva på samma sätt som ditt uttryck? Varför/varför inte?
| | === Så här blev provet i Algebra Ma3C === |
|
| |
|
| === Planera ===
| | {{uppgruta|'''Skapa ett facit''' |
| | Ni ska skapa ett facit med lösningsförslag till provet i Algebra. Ni får gärna sitta två och två och tillsammans diskutera lösningar till uppgifterna. Lösningarna ska vara strukturerade och utförliga så att alla kan förstå hur ni har löst uppgiften. Skriv era namn i början av ert lösningsförslag i Google-dokumentet. |
| | <br /><br />Här är provet i Algebra: [[media:Prov_Matematik_3c_121207.pdf|Prov Algebra]] |
| | <br />Här är ett Google-dokument ni kan skapa facit: [https://docs.google.com/document/d/1B_5J-rnJ_hwORYrYlgx290edF7Zz16kbiskccrwesaU/edit Facit till provet]}} |
| | <br /><br /> |
| | När ni känner er klara med detta, fundera ut vilka delar som ni tycker varit viktigast i kapitlet och vilka delar måste man kunna i kapitlet för att klara kursen. Skriv ner och lämna in! |
| | <br /><br />Nästa lektion ska vi titta på era prov och ni ska själva få avgöra hur bra ni tycker att det har gått och om det är någon del ni borde träna mer på. |
|
| |
|
| Sätt er nu med en annan grupp och diskutera vad man behöver lära sig för att kunna detta avsnitt, Rationella uttryck.
| | == Speciallektion 2 - en övning på begrepp, procedurer och relevans == |
|
| |
|
| == Faktorisering av rationella uttryck ==
| | {{TIS|Åke Dahllöf|[[Media:Speciallektion_2_Begrepp_procedur_och_relevans.pdf | Speciallektion 2]]}} |
|
| |
|
| | == Övningsprov i Kunskapsmatrisen == |
|
| |
|
| '''Syfte:'''
| | [http://Kunskapsmatrisen.se Kunskapsmatrisen.se] |
| * Öva på snygga redovisningar av lösningar
| |
| * Öva på faktorisering
| |
|
| |
|
| {{uppgruta| | | == Repetition av algebra efter provet == |
| # Vi ska titta på varför grafen ser ut som den gör för ett rationell uttryck. Varför är t.ex. x/(x-2)<sup>0.5</sup> speciellt?
| | {{#ev:youtube| yNXT96PN3C4|240|right}} |
| # Repetera hur man faktoriserar andragradsfunktioner. Vi tar upp hur man gör på tredjegradsfunktioner. Vi faktoriserar 2x<sup>3</sup>-8x<sup>2</sup>+6x tillsammans och skriver steg för steg vad som händer.
| | {{khanruta|'''Öva algebra''' |
| # Uppgift till eleverna: Faktorisera x<sup>4</sup>-2x<sup>3</sup>-15x<sup>2</sup>. Lösa det på ett kladdpapper för att få ut rätt lösning, skriva sedan rent och steg för steg redovisa på ett papper hur ni tänker.
| | :[http://www.khanacademy.org/math/algebra/polynomials/e/multiplying_expressions_0.5 Kvadreringsregeln] |
| # De som prova något mer får faktorisera det rationella uttrycket (x+2)/(x<sup>2</sup>+3x+1) och titta på vad uttrycket har för asymptoter.
| | :[http://www.khanacademy.org/math/arithmetic/factors-multiples/e/least_common_multiple Least common multiplier] |
| # Gå till förra lektionen på WikiSkola och titta på de andra rationella uttrycken i GeoGebra, de som ni inte tittade på sist.
| | :[http://www.khanacademy.org/math/algebra/polynomials/e/factoring_polynomials_1 Faktorisering av kvadratiska polynom] |
| | :[http://www.khanacademy.org/math/algebra/polynomials/e/factoring_difference_of_squares_1 mer faktorisering] |
| }} | | }} |
| | {{uppgruta|Denna är fin att klura på och diskutera. |
|
| |
|
| == Nyttan med Rationella funktioner ==
| | http://nrich.maths.org/7452 |
| | |
| <html>
| |
| <iframe src="http://www.slideshare.net/slideshow/embed_code/15224835" width="342" height="291" align="right" frameborder="10" marginwidth="10" marginheight="0" scrolling="no" style="border:1px solid #CCC;border-width:1px 1px 0;margin-bottom:5px" allowfullscreen webkitallowfullscreen mozallowfullscreen> </iframe> <div style="margin-bottom:5px"> <strong> <a href="http://www.slideshare.net/HkanElderstig/rationella-uttryck-och-nyttan" title="Rationella uttryck och nyttan" target="_blank">Rationella uttryck och nyttan</a> </strong> from <strong><a href="http://www.slideshare.net/HkanElderstig" target="_blank">Håkan Elderstig</a></strong> </div>
| |
| </html>
| |
| === Genomgång med exempel från verkligheten ===
| |
| | |
| Den här ppt:n ger exempel på hur rationella funktioner dyker upp i alla möjliga tekniska praktiska sammanhang. Det är bra att förstå hur dessa funktioner beter sig för att kunna förstå och beskriva olika fenomen i vår omvärld.
| |
| | |
| Exemplen kommer från Ellära, Fysik, mm.
| |
| | |
| === Nyttan i matematiken ===
| |
| | |
| Som så ofta förklarar vi nyttan av detta med att det behövs i fortsatt matematik. Det är svårare att förklara hur eftersom det bygger på matematik som vi inte ännu lärt oss men det kan ändå vara värt ett försök: Rationella uttryck leder oss till gränsvärden som leder till derivatan som har många tillämpningar.
| |
| | |
| jag använder bilder och teori från {{svwp|Rationella_funktioner}}
| |
| {{clear}}
| |
| {{uppgruta|'''Räkneövning med röda uppgifter'''
| |
| | |
| | |
| s. 65 uppgift 2234-2238
| |
| | |
| s. 68 uppgift 2316
| |
| | |
| s. 71 uppgift 2330b och extrauppgiften 2331
| |
| }} | | }} |
| | | Här finns ett gäng övningar på Khan Academy som ni kan göra. Logga in med era användare så jag ser vad ni gjort. Titta på filmen där Mikael bondestam förenklar rationella uttryck. |
| === Varför man inte kan dividera med noll ===
| |
| {{clear}}'
| |
| {{flipp|''-'''}}
| |
| {{#ev:youtube| BRRolKTlF6Q |240|right}}
| |
| | |
| Det här är en allmänt hållen film om att dividera med noll. Den passar till området men den går inte in på rationella uttryck.
| |
| {{clear}}
| |
| | |
| === Variation Function matching ===
| |
| | |
| Gör den här övningen.
| |
| | |
| Av: Michael Borcherds, http://www.geogebratube.org/material/show/id/18855
| |
| | |
| <ggb_applet width="729" height="536" version="4.0" ggbBase64="UEsDBBQACAgIAIdySEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ1VXdVRUX7QeuhukYShph+4awkFJaUGkpQUB6SEcCRliQLqFoZEu6UZCUkJwQEJSuvuN/t7749217r1rnXv2OWd/99t7f/uDrjaEhJCBEAAAkDxRV9VDv7+i7zh8XPSzAyfxKQBAu/pEFWzgO79r7uxCM0Czjvf5qjJpKM4gppTvqVmQ6hMONUMDCoKCuu04A65P1E+vcimUP42TE0ZCXryjLGMjV/GVwbWJdo0MpbOO7OspdU2z7+ymE2oQxj2uIqkWplvAWZgruv7mn9wWsL/Y0uLpur8YEFvX7GNvP5b9I+1H2n6mqOdjVEdwTnpGBoHX8brW9vY2O3JZEX/WPfZE3fH09PTxPKrFZ2u5J4LdwsKCFfXFk/sVQ5CZqamqTMWw2NqHxAdPjJBPgtbF0kDpNyK7V6c7bI6+FRkiy5ubm5G8wXUirkvtWTMV5hreb621r5e2p7/L+rw2Sescq8jU3kHW1k7xfKS6/OaoZ9Q65nA04GT/y3X2LHOGYD7pS5Zfycdna+E1NZGvRoBPNabuyQiZlOnp15LHqzgVYaVlH66ue6byD92VJQJ79uJOA/1QcGKK4sLCcCdnZ8fbq9OVYM100YjN47G2jgjf1mG2teUUj6YdYPAt/zMzRkeU5j6+gxwvryoOjioXl+rxOoVWdvkGqjHOYV3ze2tQBZS+pCWDR1b2xPTVw4nuMBlFzysiEPnvjZ0tGhrVqSKqpJQIBSqDF5pizg8mPptdvf0aEmALOR0yXldJSwFx8wlEj3CPem2Os9nTF2lzyfgnpoYn//RBnHi1gZc7vH82+xvuU1d2VGzEdzjourUV+ADGa+xUNVK2mQcDtco2rxvddm5GtqT2tyaCucberGYjh2OlguQm/vw4ObC4908ItxADXi5hLLGsSR6Lb/TgdcXGfdhDtRS9YLMIPAyrjR6Th3yfZ0hmIqO/6ewB/XZfAtvm0/0BprJG9Tc5xC9i2GJdH+ecgvbTxa8uYxhVx+SogrRaGiESqp5XivdPElOKiooKt/VlDwa+3Lx7J2TtwKELai+kw3DXTEfGPW0iO5L6tRAn96p9PVBEnpKV6tREJpr2arus0tp+Ugjz9mKAAtSngqt4cKAh/bhEBBCpxwXIbzpCxEA57Q7Ur8/347IIWGEpL4/eShv4XRQwDTGrOtH6qrP28ybjrm3tNkLNY9cyrYVJpKUxt+C0VNALtg6BpdATfOrCdZLip25Ndk3uy5jMcr6Is90FiKzPntjk+R6K8Xp99iXHfO1A475I5KnwCR3nO/POEpLViR+1FS4sVonxn8Ykh4dOtiKoauakwwNGiQAfRuNzcnRw9Or/UMPkrgUmckOThSNzhCLrnnfq4u/GG3VBdQPSdzF1MXoadA1pnFSEFvgRZPeMDNgLoRs5ZI3SqccZOa7akj9evu9f6aM9xXVrCE3dZXz1Q+AMESQnmyBvi1//cBPo5+fXLcXDW/igrDJuU3ZpQvy5wswdZ/QDojZNUjWAuGWUGIG7O8mG+r7fKknemff27bDF5uHSvTZU1lt3gPUOyOC2n3OnipqXx6LinmybMdqeZbBaqnP8Dj1/ROLgd9Ufkx8afAPzfyCQu6gGd1Aavv914mi1EnwxoKjHfeQYaEUFvhuobFVuE7Wf7EzgUk4O5dXHBh3Ee8fdLd2//Dpz3rK0VeMc0woZPjbZEcrT3JTSL5pU2Q2+Rz75Di/5cNY6+pF76zDDTS9u5uv729XT2ZKSkg9XwZcan/bafDZiERhyzS0tYdG/lipjpNx7IhPD8z9/1kIuMxwBSWZtCpaljSteUACgqOa3tsbc7FoZ6fJ3gzrRMtUz+mVnexzT5gLoyN81ZR4WkY5fynxo13cdzdMB8w4XY5oRSxtzzPo5M5+geazHvQchF3sY+MVStjPUs8wcgAuO5rvgS3fFh50Ryrx9yhqKPGWiHly3HAVNKa17le3iiIAVakl6R6YEMvRl4UtKzeFmLFqpSsZWuVzE/r/ZUkDmzZy+ue8Ocz6A/ZVDu1OB0Gk+mdyYICwsrHnievDO8bDyo/35eo2b9fV1Qhq5RIwXrEGALWLCiAHd4hgvNd1jhqsPuhvjNTUiJIU0U/Y50PUXriOnwl7Mqk3pvblUjTpNuPquZAvFt89abuVv5b3KdpIFyV647b0ubL9TMA4Zdbz7hBkmDG6WaJuHO34ugCUmJzOcsyoEmmhWAuM07REKmszYFXN+YX794zFWNwffevLARnVGkXWZw9J1mztqdS1WjW9eThqwM7SNL75YgCS5Jj3GirM9zAz2ULB7MZQbVvRAz8rm09c4CzmiRI+HYXf6l6zxeI6yZT5Rcnrhv2mG1e4MDcuKL4yqv+ov6r2+UW7YPnOCSdp21toGpe2Fh/clKLwiFg+6FReXkAjnnJ2eDhsMGV0uiK/iMv8EExg11cwXeTzRD2WMqTulndV/CWV5e7ZdOlCzLjLBG1vPJMrguf3DgCN4GsWX/lJGftvTvcOl6iOcW79rGnOCTcJoZ8z82Rflg97aeON1x00HoYoi4yK4s1Ry1vPHaeJp/SDboYphiT2qqYDd5yId0igQELqXKX2yPVddZzNA+ngsCGerwF5jSzLnJlw7U94q5IQxS9JhZuL5M8aAu6TA0hYLezFVscmrWH9jS755A0F6pSv7+ztJrcvLsS1nV+zDAOkEBmSKhHzarLUfe6GgR92B8rhsWQIfmeJXAN/7+O+xHp5vFcsBiRzPtlW+wHpV9AGr0caY5I2rVjg/JwBNUcR8cpZaY4nwITE+Pr6asVan6Y+n4gr8kNb/Eplt8U9UqCIgmcuyn8cOd5TSZUxBwixzv3IBRI2hNgtXZQk5yDqVjfE8wCpEnKdh3Ku/6y4vF3gKW/5OoO5TNZKMQkHokGay6nL+jh3Tg2/IiwAhWD7q7q//LoW1FDJjbsItgylDLGZG6TLsSdD57XwZkauQQHzIAxF4qqMzixvGnY8pF+hK8FpitqLPHFfx6G8K/nIaTzEVcsXOsTtvGfblMF64aJn2TiX+xkoiZ0lgMvaFNOU6h83pYdetd5Cid5DGutjFrslt8s8r6y6H0m14vVUPrllHwR3rrfpFgho/1U2xAbR67drgsK/7OtpAR3uB3rf0yvqTOUklKJlE3V5XihjIvLcL6mBK9RBSPydQ1xHTdSCarFZyWuntTISBmzUQLN/CMfibotKl4pU+Car7NI0kg5t1wM1RLYPBbrezTaAfYPTwgLbgQgNOIRMB1qShLP6ZOE5JUwaTi5S6+LlTIuGkY23366a9OFqyOTV2yoZLaT8Rod/qiVeRjOrGbyStdDcByDiWz/sHX4HyqUDzPtR7sBUxIlbwccd5m1LSvzOM5upiILFSNFPJi9HHbIwG3vQd9WPBM2qqV6F1FNjJ3hlZ1H7Yh5f43eHK4izopFf3ZrV/kw67WknhikfX06cfCOOsNykXP+zn4OaGqCYlUD+Dh21Nh2KF+qWAK+KqSPO24WFtubYKle0mr2+C/gRWl7crvYZWl1+2XlgPBhgGVku4LTI9vO8kAumOHa7GDlF/3gsv1Wa/tE5bKqO1ELi8Q09xj24CJVMhXtfn2ZiH+7VJwrp5gMx0ZLK8Mr3+xJNQ/EmU6UR8R35RT1Wh5KKbra4D3uSyYIyDHgY/HsyLSt3HWS3FWQYpngVm+wHzKvat3rHpHOoCorD/2n1riexMfzmt15c7TopUCfjtNeCPu3WIt1XKjN2Tul1I8ofJnkVIYDRqv92Zkah37LelvRotMAv8CVN9QMQswwRIPImFOUlPTcqmDhEzow2kR16TI0V5mNgRsdInc9WhAniwE/DKAZ6TnBBmhuAWmyy/NZwVm4dwroXYA9rbBhMqiaN79c3w62Lr+MsuMrhjbyT4Cn84hLQGP76GPdRLoBZVw4X4JWGl1FwKMtLQgMePjULWHaYmEHWxo6SlTfpWF+2WiiXm9S3FrSU/a0HJiWNloAeBQ2hqIirQyHdKht+sDugXSTQ38VKt1BdfWS+zGFoIbOVvTNMSdZS2mzgYc+zBcdgMzLUY9iQid/gYJTlt35cUZXsUrJzqSyfIdCfSIMua03MbV1iSYhgpH91gPH4lUPu2pNQWsaeC3sKJffW9UJqSv12BMw3oo45S86UGSKWqpCldiAfpjiB139PrGwZC8ZWa+bC4wXI2FHgxgcqPycfOl2bXC3lDBSGTuId1lBGhLOyIPTB6JoobiNJ0ecKKhk9Nz34Uu4HpCclkWjgGMo4+37km9R3e5LfeZC9xFhwcnMT4eArCyUPtCTAm8Wt6ZEsnkFvbqy+T/wG1FL+mmRlrfaNiQ5abt/eZ8/11vlyZBZYbVux6GRSK1SOyIb4P5xLCz6QOvl5QGkPRw4gTqASNtLUZkxLlyGPMskGmXnDv/de0GzQ0zGKOerD8jW85wfrXKw2T3WGSJVUHLIZG3vClPHbUblBf1IMJtuEhlkjtxrfO/EkpPk5j4+Y5xp+btYZTJBnPnyoU6SzRHv36Ovqa6vKNYgWzwk+rtbjGGdvFVr/EnBy3TCLBB51f8EiSc+oUCfL7jlbgdtotgZc18a82OGq9trQ+t1cyOEaQQlUWGlATQWaqQb21GZL7pRysadHRGXnPgg+6xD/rTzvH7DD6398+vlr7uMNuYWXFWN/gPbV0Z6Tj1jZd/Ns19+TkVennaRu6wkKJqQSu2c0YyUdTFeaf342tDZKYZriMy+gT2dmhCn2WXHN3F8z6akVEM8LKqbhnnKZyzorbTQ4U9U77TBtfM8tni8PvUj5SGXFrB1aTp+igOfSG1BBanZ6enjfEWpY1aPKB7x+lVuC/k4Ws1zYa9c2zbhERFH38fendOKTIHqVN4AN8fYCSTJnf6rBKsV8O1MhCi+6XR1X6LI56nGRqFHb2ZzlrjD/r64uIwHYRamtm/84uQZgXLZDZQF8/3yq+rc7NIowyFfMOMP7oESnOKCS2jkhN6dkEND7ckbnwpdTIJaAJY95+rP3R6NTka2dA27BkbhU1AHpz0QlbQL4VLynxUy8oIIu2Od8LR3i22ByuyIs5GeDcrtB+sZolZXJoaCMbE6WSwWNQJA1xLmF5+aXmmRemWKDDF3fot3TZOu/dLETgcLK4Y6dZB+nVL9h6l/ZpzNFwdMTi7drN5dVLEw4erAXwitQ7qX2TMw78KapmGbuofPcxTeLJj5TUi353fsayvCLq9ohsg9yqHTxF9zZ00vfHDPHCDYsnMLv78/OLvuLWTv6dW/BCbVQKuJlMqTlp7vmzGLyfmr+qeDa7cfwPelgfYjfZIbSP8ova7x1F9h9mp6RAdux8YTC8kt0+Wqz7R7AXrAmjOYo6bW1tYqXNzaYmbssrAAug1HCXSdi9eo94Joe83vwAa7AL0opKzKU9OnCun3UqwsTxom8mQ33gbdpDH6a6QrUEGscMCVdCjY+XeYOgqZny51QJ4RvNvFSxJIwSvYlLFZoLDa75KlQPx+NzbgU0gyTtlO1r+YumZEJ9qgX+fydbrNPSsFGnPV4xsjuilfXnRy1EQEWXBczH9326gbaupE/9+ABGHMlpGF7QAAZBML/jjVDW19dvM7/vYe2Nj5B4l9n1iuS/DzLqL8Ay/mVM88Sfo/GEwq5FRUXlsWp6Isj0vb0bKHNr95r2kiPeJuXaMIiGtzMItKSc09HSa8q1tkf4zkTMngH9iuuGm0JPjo48lgPI2JTrRB51UV9YkmYlJ68TIJbvzhcDQLZh2bT03n/mKFj4x8OITXSWTXGje/MhjGxzra0QfqHTI5YRuXLZsYDl+PT0UgPW58+fZ8/D1jAMK2e96VNI3wGzRSxlsQkmhqQ46V0oOnzTAL6vnzw6wJg7PZoWHQYAHRbfoD4Te26Mkjzn2oysgg16jtGTTA4HiKX0NOtNEJHtjB6/9F1bW+OZhvj7NxedWa4v15v3F8Dc35dIHX79RgOUFyD2AizZKX+HtMrgw06kDkNgeWdhRPBnX4FQVb8qLhRIhPhRLQncg7HTJ438lEIHUfF00OWLeJ0WqEPTa9fUN/ME0D4MnIW8kMH3Hm0qNHwYW2ZcGSVmsvZsIlUlR+pNtzCoGMDIwOBS/wjgB4iqNkimRBgaGk6U6BfJYcnQeAxzqK6GWUrDomKXE7sq5W70SHWYsZtdi99+6nJyaX04mTsKe/P7ZGuqzrqP8BO0uKwsPyGBcqLJ7WcTGI+UidzTpXgxCg4nEcRhwBc40kh5RNP6xtx081OMsCQPuQxQhv1iyD4EzzZdzq/GXUtIcTZzVoeGXfzltaTrJAQBjiHyIWd9Sw66toZe/k7REcMxbyY/PT3tJocRWrT519MtotWEgPWeFcPZqOx+5H1O0FVJOEQRuToQRxT0FUuc5QRl1uDyKYnfeBLdM5OcHmZKezrszHyeP7lBHoyFytEZVgVT23aLiwXJYVVgED0QIHf0EOv2nCCIpx1r5KdqXysVJvwd4NmCp2/8nP7t7dXssjDh4G27iYi2NdJDBkVLdGl4/lcOPgwu98ZdLL22lvc9sLQ965Px2Ss/vO/CgnZRl2elPhI0a9AUs5SWV5aRIV2fn7QUdZ0XWw16AUkfgYPuyp/r5BmmQcg3p7rwZFx3RMcnhGqQSGRk4PpG+vEVJbUTs8mjWjtEtiVQngWuN6LEql9uMxDLe4ifafqmnzjPdaHXwuj4YWp6CknYm1+Hkxr92lEuPCfG0isrTt25uvEDmxPNoAewk95x674AOg2ntgDnMpY9P8Qc6UqlRxUXFGmnFJEq1CX1b4csaDW1n2XZxNZUjD7uFjFa56Q7dmHmxSmIaNMjRdEi1yGbu+OKD3p5ttAvDfNCTyHEI6gQPc8OSn9qVPkKMYpWSlZztBX1SSzBO2Z1tsvKuFvoxuUvitTDMXHR0iQdB2lvdv6qbuFrCulTMwZHi/IBWpDevU4wA2U+AlpN2UkLB/tn+lrS+mg02eNuEeBOSt+EYpJJ8SjD7dgp8oV+7YtUnQpTM79/Ero+wnZ1c4zgpPidPCjZC4Ry2nWy82oIkONuKWBtlRJLKURikqnW1hcPVjOIbP6fGYem3xoGx8xctdUgO7FX55IdcActjMdsO6/IXE5t2P56nabkzouh3kj+n4NgXt7uj7PN1//rL7iy7fGGcSXpQkw2WAY9FJZblJ1XMT9fhdpEa0FiZBm6fYhQL/Q77UsIsCy5sF7WPex7VwNGl847SOxNUHq6w6/rJTLejyd93Q9u0dXT1dV1qN1ECi3gkEf9ZaDkcn0aC4G6MorzPusjpaQk9gfqnNb/cGVL/jGPvWP77zcJR+Kx4H8nEDTCtiZeESXuNi2nQFhtG8jnGWBbCxq9c6z2jfodivdC08Xa95iav6vQRJMFn7Gvvk5IXQcXMdpu8sivsw06Qrcw/Af+uxLdB7C+pn+q8aE/prZtBL2TvwdMGR5Fe23Jlkzwv04f/DKvf3rT125SlVlUUCCMLmijnPjOSrEsNMHoWgNRe59rg9jT/7t0zw58+n5E9LsiD/+1NVcoyCgPdgKJY6H/VME16NBihI6MTDqMAw+QeTP1JdgkgiWMDk0sMmoe1c3t0FCMVSZhFEWxGCWbJQ+PpKSxZS2RkQ3QoPWZmAmajEg8UuohX+bIVDhPM/B9lsTH1vC5fSnbpi0hudAsag6BWnEq2Ak21taH9pYAzp6sP8CCKsdUfNlaGwLBQuML/+eVzgAOTjSeKyjUrSFpLBnl6l1//+M3qnnNzTJmLJtM62x3K33wurUkY4e4GNpKzlgydIgcrE/3cKoEBSnEsCpmv2q/fGXA0upX3zHUJUwY8SQ83XOD57hlqcCGi+uZn3u0cjC6y7pyH9TVp3rDrfZfBL3L7UqXmpAKI6QLYUrFMhX6O/qRkTrdOrRz3Pf6zHVCOkQLefseTaaTNZww0Veb2a0wmoh42iw2EEinKQXdS/Kqb9CF9VDlu/8y7siDMLRX8VMN8GiO04URTzIfdfIpZ9g1/EWHW5LnPV/giQNE7i+kOgq6vuvRu9pRRtb/KCMbicUyhzX8ilttD0iwCEYTJATy3n1Mru9pAu8DmBeeXNXIDOVeGtg/IcTrrM+jk0O5yV7W2kIA7RFJWA9bz5RORFhAA4cE9VUZE/FkhCmuJthGAJ2XRoHyfmC2hosP5Gjj/wLi5CR12AUdDI1M93gv38knSvMCUAD09URNW7VC2fLd/wBQSwcIs2PmUvgXAAAcGAAAUEsDBBQACAgIAIdySEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICACHckhBAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1a647buBX+nX2KAxcIkmIskxSpS+LJdmeCtAGSzSIzLYoWWYCSaFtrWfJK8owd7I/923do0XfoI/RR8iQ9JCX5NjOxm9kkg9iUyEOecz6eG+kMv13OMrhSZZUW+WmPOqQHKo+LJM3Hp71FPeoHvW+ffTMcq2KsolLCqChnsj7tcU2ZJvjghjERnPUTGXp9rka0H4SM9Ec0FioaxYrRsAewrNInefG9nKlqLmN1EU/UTL4qYlkbxpO6nj8ZDK6vr52WlVOU48F4HDnLKukBiplXp73m4QkutzXp2jXkjBA6+OvrV3b5fppXtcxj1QOtwiJ99s2D4XWaJ8U1XKdJPTnt+QyFm6h0PEGdvCDowUATzRGQuYrr9EpVOHXj1ehcz+Y9QyZzPf7APkHWqdODJL1KE1We9ojjM0I97pGQCJeHyKIoU5XXDSltWA7axYZXqbq2q+onC3IP6qLIIqkXhF9+AUYYgRPdUNswbDzPDhHbR1zbMNtw2whLw+10bkm5peGWhrs9uEqrNMrUaW8kswoBTPNRiZvXvVf1KlNGnqZjrTw9QZ2q9D0SuwStxCKO/YSc6I+HH64HBttK0g2udbk4kmnL0qfu4SzZJynqtjwFE/s8mbhFTe8OplbvQ/SkYgNaZGX+mc8eR/cuNXc52vdPY+jxz6LicNC6yrDxDqgmmraxnlrNKu0vbggi1GZPQaBveD5auQAaYuMzQG8AKoALfKUBeLr1wfVxgIMLAWg66oJxDhHgF/fNYh4IXEz3+uiTQJERB+ECNT7FAT0JjF+ijzIXKYQAgZM0e8r0Eq4H3MM3NwCOMmqX9CkSujgR35E9A5eCqydTH5gHnl6Pcu3qXqBFxyUZeAQ8qhdEr0aPtt6M9AG4WhuvgSvN54t6C6J4lrSPdTHv9gKpMR6tg56NT1sx8cEwk5HKME1c6J0EuJKZ9gjDaFTkNbSbGNi+cSnnkzSuLlRd46wKfpJX8pWs1fIFUlctb0MbF3n1Q1nU50W2mOUVQFxkpJO5yOjGM+ukxhd3Y4BvDoiNAW/j2b+Rb4EjsKgU8i/KqiWXSfJSU6xDAyL5Js9WZ6WS03mRbqsxHJiMM1SLOEuTVOZ/QWPVXDQu0CUgHa7aBCQobQUpyuRiVaEFw/JvqiwQWuE5PFz/YR5Z2REmhIM+wZkIXOYxF7e7iqV2PRY6Pgnc7g9HVu0QdVhIPZfSgHiU+5avuuq2Ry5Vp/m4TJPN55fVWZElHQ5G9XM5rxelKRtQo1Ir9F0+zpQxD+PUmJPjaVQsL6xduHaty9Uc34jlH40N5FAarZCgaSPbGhotWEdFDA0xFKQ1tDTpxmnIDIVpI9saKrRcK1qjKG21pKRlk1YmmJHelssYs9cZfpGn9av2pU7j6VpTTf/9Yhapzni2l6T3tORwsGNcw6kqc5U1towbuSgWlXXNDTNPVJzO8NUONIBIvVl/RgFsb6LGpWrlzkxBZuEyo2TTTPe6zVIvymL2Mr+6REvYEWA4aKUcVnGZzrW9QYTxf6rWNpWklcT0kWzO086Hqsc6TSA8tYbmxSK3739cqKpSJbrpop4UuPWv03giVQZnOICmhyMJRhtE1lSBRTmtJkrVl2pZg4yKKxx5rmpVztAw4Hoia6gnCtTPC5OVoBiZ91IlMGpZptVTa+h93IR4agiiTOJTRyLzBO2+KCoFH379J8YWjKJ1qqoPv/4LIy4OIVZqmxN21+VKN1hox5OOrQmgzsPfUfLUfF0WMFZWylwr0fI80ZELHmb10/PLt68ejuun/bfrWegFKtOmtwvPmmRmR/4wi5ohJy5mzQbMZlqj3CTyt/iIA+vMIokxVUk7oyoWdTsg7dY3S+i4mKkZlsFQmwCQL2aqTOPOGaRZFw1n0dgWcxrrKqKfbnF/kNl8InXJTRvvsCyOkpzvSZ4fJ3m+Kzn9TJLTfdCn9DjZkX5H+PAehX852hE8hw//+Dc04j/q08c/PpKP4fcwpfi1xG6mJ/3dkrET2CP58RF7fAIdibtLMoDlxjC/YViv8O7duz3kRncD1zpbh5xVTUdpQKSwTNoJ7hvhdxPJNsvtY9nAnsmVKreiq1nwdZFsx9x1PquxypriURLzhN9rxCX24U9pkihTYe/s091WEe0aBW+lO1pfazlUuDfbzgH6NnRVpo/XgNHa2P9MLs0pWUYV1oy1uogxe+Xr+wUrW1NzUabhBT0j0A8rXaWaC41RulRdpYNZJH2PWXQne96INLsLaZ0RMeGa6I4l3dwm9LlSthToJs5ReVNAbaTKQ/doemvUuX2P1pXJbc7NCL+fLepjcLKbpB8O2yXS7ZJodom59M5dWiv0xTZpOS+Rl16kBRlzM87HgdPew58XRf10BacwhaV9MQtsb62e0duefs++dmRsqWpZ1j/oIh/0dvRDJ6TUC0LCCfOZIJ7ZnMAJXOoHLBC+HwYEzyfvOyv8OETsJoj++5/DQWJfHUhByJkrGHMRJiosSL5DKKGex3yXBRy/j0PJvQGlwTGm5H51KIWMaZOh3Hwzg5JwmO/jqZS6nKORef5xKPGbUTrGmvhXh1MQhnwNlIHJdQQjaGACj/DYJ8itOH2kDotseWTrsOlW7RW1hdV0q96K2pJs2tVYtos2XbfVVeMj66rx4RuBx8MktfFbX8w01PHh5et9lFyiTRVUfKzm2rPd7xq7fYQgjh7Rx4/btcwFi72W24arGejm/z/5Xl/Wjm0T2eZoQNjGdUCl7ZU2CVufHjZM8sHQCKwvgLbuC23vzj3C3VidtVj1DVj949E6+7xovRmNKjyua2f2uQHnQCz7LZj93w7N8xZNocEUR2N5/qWwpDYQisOgbOtIW1D+Jkg+7+zSQNk/HsvnX9ouXXagYbZw9u8Pzy1coqLIlFzngnj3jLMR/D/llHN4DliDpX8j1SeSwL8rRcRybhKS6bvQIr5eQXtleVgxI7aKmRcpZnGJ65WpPaqsrw31laW9v9PXhqrau688vPoRX/gyw/x+VOH5drT+rcX8aECaHw7XZ8ydOokSx/yKr4/01KE+1t2k/aPHVZHeFvAXeCSEN7l6Auf2OhfRNWhrCPXtcLclzuE4e1+4yjQHaduz9pJbwe97H0PfdzjjbeKn3PeOQ9zfR/zyungC63t5i/jEaLEwsE+PgNv/FLhvuhC5L7P+OLKe4zOG1ozxRlBfuPacRJ0w4HgS54ITSn3ObzXxweZvJ+a3yeZ/2Tz7H1BLBwirQA8dcgkAAAIkAABQSwECFAAUAAgICACHckhBs2PmUvgXAAAcGAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ1BLAQIUABQACAgIAIdySEFFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAADwYAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAh3JIQatADx1yCQAAAiQAAAwAAAAAAAAAAAAAAAAAmhgAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAwADAMIAAABGIgAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" />
| |
| {{clear}} | | {{clear}} |
|
| |
| == Förenkling genom faktorisering - Wolfram Alpha ==
| |
|
| |
| == Multiplikation och division av rationella uttryck ==
| |
| {{lm3c|Multiplikation och division av rationella uttryck |73-74}}
| |
|
| |
| <big>'''Kom ihåg:'''</big>
| |
| <br />'''Räkneregler för multiplikation av bråk'''
| |
| <br />(3 / 7) * (2 / 5) = (3 * 2) / (7 * 5) = 6 / 35 Täljarna multipliceras med varandra och nämnarna multipliceras med varandra.
| |
| <br />'''Räkneregler för division av bråk'''
| |
| <br />(3 / 7) / (2 / 5) = (3 * 5) / (7 * 2) = 15 / 14 Täljaren multipliceras med nämnarens inverterade tal dvs 5/2
| |
|
| |
| == Addition och subtraktion av rationella uttryck ==
| |
|
| |
| {{lm3c|Addition och subtraktion av rationella uttryck |75-78}}
| |
|
| |
|
| |
| '''<big>Kom ihåg:</big>''' det måste vara '''samma nämnare''' när bråktal adderas och subtraheras.
| |
| <br />1/4 + 4/9 → Vi förlänger så att båda bråken får den minsta gemensamma nämnaren.
| |
| <br />Hitta mgn genom att faktorisera:
| |
| <br /> 4 = 2 * 2 och 9 = 3 * 3 → Mgn = 2 * 2 * 3 * 3 = 4 * 9 = 36.
| |
| <br />(2 * 9) / (4 * 9) + (2 * 4) / (9 * 4) = (18 / 36) + (8 / 36) = 26 / 36 = (26 / 2) / (36 / 2) = 13 / 18
| |
| # Vi förlänger så att varje nämnare blir mgn
| |
| # Sedan sätter vi på ett gemensamt bråkstreck
| |
| # Till sist förenklar vi i täljaren.
| |
|
| |
| == Ekvationer och olikheter ==
| |
|
| |
| Sid 79-89.
| |
|
| |
| ''Kursivt då ej centralt innehåll.''
| |
|
| |
| == Ekvationer med nämnare ==
| |
|
| |
| Sid 90-92
| |
|
| |
| == Absolutbelopp ==
| |
| {{uppgruta|'''Undersök superformeln'''
| |
|
| |
| Den finns på sidan 83 i boken Spelprogrammering med Javascript.
| |
|
| |
| Du använder Javascript, Wolfram Alpha och Geogebra i din undersökning.
| |
|
| |
| Redovisa några snygga grafer i ppt. Ange dina parametrar och försök förklara varför kurvan ser ut som den gör.
| |
|
| |
| Ta också med en definition samt en förklaring av absolutbeloppet. Undersök hur superformeln uppför sig utan absolutbelopp.
| |
|
| |
| Kan du fundera ut en operation i miniräknaren eller datorn som ger samma resultat som absolutbeloppet utan att man använder just absolutbeloppet?
| |
| }}
| |
|
| |
| == Att bryta ut -1 ==
| |
|
| |
| == Diagnos ==
| |
|
| |
| Ni skapar en egen gemensam diagnos och utför densamma.
| |
|
| |
| Ni rättar varandra.
| |
|
| |
| Efter det berättar ni vad vi behöver öva mer på i grupp.
| |
|
| |
| Ni gör även individuella studieplaner för nästa vecka.
| |
|
| |
| Sedan kommer vi att börja på nästa kapitel - Derivator.
| |
|
| |
| Vid behov kan vi återkomma till detta kapitel.
| |
|
| |
|
| == Lektion 5 - Programmeing == | | == Lektion 5 - Programmeing == |
| Rad 228: |
Rad 112: |
| == Diskreta och kontinuerliga funktioner == | | == Diskreta och kontinuerliga funktioner == |
|
| |
|
| cvnG0YWPLjQ | | {{#ev:youtube|cvnG0YWPLjQ|240|right}} |