Lektion 3 - Kvadreringsreglerna och andragradsekvationen
Hoppa till navigering
Hoppa till sök
Första och andra kvadreringsreglerna

Kvadreringsreglerna är regler i algebran om hur man utvecklar uttrycken
| [math]\displaystyle{ \ (a+b)^2=a^2+2ab+b^2 }[/math] | (Första kvadreringsregeln) |
| [math]\displaystyle{ \ (a-b)^2=a^2-2ab+b^2 }[/math] | (Andra kvadreringsregeln) |
Texten i ovanstående avsnitt kommer från Wikipedia.se
Förklaring (a-b)2 = (a-b)(a-b) = a2-ab-ba+b2 = ( och ab = ba ) a2-2ab+b2 V.S.B.
Länkar:
Bondestam respektive Wille på Mattecentrum om kvadreringsregeln:
WolframAlpha Widget
Här kan du testa att låta datorn göra parentesmultiplikation:
{{#widget:WolframAlpha|id=c3f53c80c93fa003e2f8f54c64e0e386}}
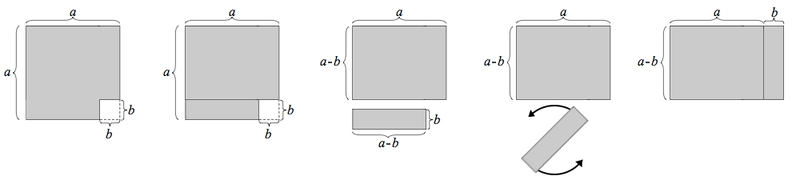
Konjugatregeln
- Så här ser den ut:
- a2-b2 = (a-b)(a+b)
- [math]\displaystyle{ (a-b)\cdot(a+b) }[/math]
- [math]\displaystyle{ = a^2 +a\cdot b -a\cdot b -b^2 }[/math]
- vi kan stryka ab - ba = ab - ab = 0:
- [math]\displaystyle{ = a^2-b^2 }[/math]
- V.S.B.
Film
Bondestam (tv) respektive Matteboken (th) förklarar:
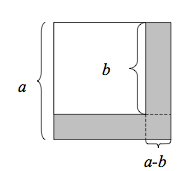
Geometriskt bevis av konjugatregeln
Första beviset
Andra beviset
Visualisering
Här gäller: [math]\displaystyle{ (x-y)\cdot(x+y) = x^2 - y^2 }[/math] Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit. [math]\displaystyle{ (a - b)\cdot(a + b) = a^2 - b^2 }[/math]
Uppgifter
Övningar (utan räknare)
1. [math]\displaystyle{ 1992\cdot 2008 = ? }[/math] 2. Lös [math]\displaystyle{ x^2-1=0 }[/math] för alla reella x.
Tips : Använd konjugatregeln och nollregeln för ekvationen.
Webbmatte