Algebra Ma3C: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| (155 mellanliggande sidversioner av 4 användare visas inte) | |||
| Rad 1: | Rad 1: | ||
== | == 2.1 Repetition == | ||
== [[Lektion 1 Geometriskt bevis]] == | |||
Bokens introduktion till kapitlet. | |||
== [[Lektion 2 - Repetition potenser]] == | |||
[ | == [[Lektion 3 - Kvadreringsreglerna och andragradsekvationen]] == | ||
== [[Lektion 4 - Faktorisera]] == | |||
== [[Lektion 5 - Aktivitet Geometriska bevis]] == | |||
== | == 2.2 Polynom och faktorer == | ||
== [[Lektion 6 - Polynom, faktorer]] == | |||
== Lektion | == [[Lektion 7 - Faktorer, rötter och nollställen]] == | ||
== 2.3 Rationella uttryck == | |||
== [[Lektion 8 - Förkorta rationella uttryck]] == | |||
== [[Lektion 9 - Mer om förenkling]] == | |||
== Lektion 10 - [[Multiplikation och division av rationella uttryck]] == | |||
== Lektion | == Lektion 11 - [[Addition och subtraktion av rationella uttryck]] == | ||
== 2.4 Ekvationer och olikheter == | |||
Sid 79-89. | |||
''Kursivt då ej centralt innehåll.'' | |||
==Lektion 12 - [[Ekvationer med nämnare]] == | |||
== | == Lektion 13 - [[Absolutbelopp]] == | ||
== Bevisa Pythagoras sats == | |||
: | [[Fil:Pythagorean proof.png|miniatyr | right]] | ||
Till höger ser du ett geometriskt bevis av Pythagoras sats. | |||
Frågan är - kan du bevisa den algeriskt? | |||
{{clear}} | |||
== En övning i att ta fram provfrågor! == | |||
{{print|[[Media:Inför_prov_Ma3c,_Beskrivning_av_typuppgifter.pdf|beskrivning av typuppgifter]] som underlag för att göra provfrågor och facit}} | |||
Ni skapar en egen gemensam diagnos: | |||
<br />I detta google-dokument kan ni skapa era uppgifter: [https://docs.google.com/document/d/1XHvoOU061d_Uo39CHCMkgNgdsGvWJEu90K77grod8xc/edit provfrågor] {{print|[[media:Inför_provet%2C_exempeluppgifter-2.pdf|Provfrågorna]]}} | |||
<br />I detta google-dokument kan ni lägga lösningar till uppgifterna: [https://docs.google.com/document/d/19Ceh-bUUyRdtSRiTm09Ar0VuT23HOZUeHvcXrxfOH2E/edit Facit till provfrågorna] {{print|[[media:Inför_provet,_facit.pdf|Facit]]}} | |||
<br /><br /> | |||
Här lägger vi upp de färdiga uppgifterna och lösningarna onsdag 5 december som ni får öva på till lektionen på torsdag 6 december. | |||
<br />Vi tittar sedan på lektionen vilka uppgifter som ni tycker är svårast och löser några tillsammans. | |||
<br /><br /> | |||
Utifrån era exempeluppgifter skapas ett prov med liknande uppgifter. Provet är på fredag 7 december. | |||
<br />Ni får sedan rätta varandras prov. | |||
<br />Efter det berättar ni vad vi behöver öva mer på i grupp | |||
<br /> ytterligare några exempeluppgifter kommer under torsdag | |||
<br /><br /> | |||
Ni gör även individuella studieplaner för nästa vecka. | |||
<br />Sedan kommer vi att börja på nästa kapitel - Derivator. Vid behov kan vi återkomma till detta kapitel. | |||
=== Så här blev provet i Algebra Ma3C === | |||
{{uppgruta|'''Skapa ett facit''' | |||
Ni ska skapa ett facit med lösningsförslag till provet i Algebra. Ni får gärna sitta två och två och tillsammans diskutera lösningar till uppgifterna. Lösningarna ska vara strukturerade och utförliga så att alla kan förstå hur ni har löst uppgiften. Skriv era namn i början av ert lösningsförslag i Google-dokumentet. | |||
<br /><br />Här är provet i Algebra: [[media:Prov_Matematik_3c_121207.pdf|Prov Algebra]] | |||
<br />Här är ett Google-dokument ni kan skapa facit: [https://docs.google.com/document/d/1B_5J-rnJ_hwORYrYlgx290edF7Zz16kbiskccrwesaU/edit Facit till provet]}} | |||
<br /><br /> | |||
När ni känner er klara med detta, fundera ut vilka delar som ni tycker varit viktigast i kapitlet och vilka delar måste man kunna i kapitlet för att klara kursen. Skriv ner och lämna in! | |||
<br /><br />Nästa lektion ska vi titta på era prov och ni ska själva få avgöra hur bra ni tycker att det har gått och om det är någon del ni borde träna mer på. | |||
== Speciallektion 2 - en övning på begrepp, procedurer och relevans == | |||
{{TIS|Åke Dahllöf|[[Media:Speciallektion_2_Begrepp_procedur_och_relevans.pdf | Speciallektion 2]]}} | |||
== Övningsprov i Kunskapsmatrisen == | |||
[http://Kunskapsmatrisen.se Kunskapsmatrisen.se] | |||
== | == Repetition av algebra efter provet == | ||
{{#ev:youtube| yNXT96PN3C4|240|right}} | |||
{{khanruta|'''Öva algebra''' | |||
:[http://www.khanacademy.org/math/algebra/polynomials/e/multiplying_expressions_0.5 Kvadreringsregeln] | |||
:[http://www.khanacademy.org/math/arithmetic/factors-multiples/e/least_common_multiple Least common multiplier] | |||
:[http://www.khanacademy.org/math/algebra/polynomials/e/factoring_polynomials_1 Faktorisering av kvadratiska polynom] | |||
:[http://www.khanacademy.org/math/algebra/polynomials/e/factoring_difference_of_squares_1 mer faktorisering] | |||
}} | |||
{{uppgruta|Denna är fin att klura på och diskutera. | |||
http://nrich.maths.org/7452 | |||
}} | |||
Här finns ett gäng övningar på Khan Academy som ni kan göra. Logga in med era användare så jag ser vad ni gjort. Titta på filmen där Mikael bondestam förenklar rationella uttryck. | |||
{{clear}} | |||
== Lektion 5 - Programmeing == | == Lektion 5 - Programmeing == | ||
| Rad 88: | Rad 112: | ||
== Diskreta och kontinuerliga funktioner == | == Diskreta och kontinuerliga funktioner == | ||
cvnG0YWPLjQ | {{#ev:youtube|cvnG0YWPLjQ|240|right}} | ||
Nuvarande version från 1 december 2015 kl. 10.26
2.1 Repetition
Lektion 1 Geometriskt bevis
Bokens introduktion till kapitlet.
Lektion 2 - Repetition potenser
Lektion 3 - Kvadreringsreglerna och andragradsekvationen
Lektion 4 - Faktorisera
Lektion 5 - Aktivitet Geometriska bevis
2.2 Polynom och faktorer
Lektion 6 - Polynom, faktorer
Lektion 7 - Faktorer, rötter och nollställen
2.3 Rationella uttryck
Lektion 8 - Förkorta rationella uttryck
Lektion 9 - Mer om förenkling
Lektion 10 - Multiplikation och division av rationella uttryck
Lektion 11 - Addition och subtraktion av rationella uttryck
2.4 Ekvationer och olikheter
Sid 79-89.
Kursivt då ej centralt innehåll.
Lektion 12 - Ekvationer med nämnare
Lektion 13 - Absolutbelopp
Bevisa Pythagoras sats
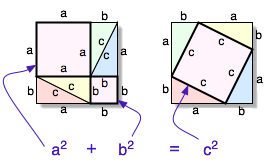
Till höger ser du ett geometriskt bevis av Pythagoras sats.
Frågan är - kan du bevisa den algeriskt?
En övning i att ta fram provfrågor!
Ni skapar en egen gemensam diagnos:
I detta google-dokument kan ni skapa era uppgifter: provfrågor
I detta google-dokument kan ni lägga lösningar till uppgifterna: Facit till provfrågorna
Här lägger vi upp de färdiga uppgifterna och lösningarna onsdag 5 december som ni får öva på till lektionen på torsdag 6 december.
Vi tittar sedan på lektionen vilka uppgifter som ni tycker är svårast och löser några tillsammans.
Utifrån era exempeluppgifter skapas ett prov med liknande uppgifter. Provet är på fredag 7 december.
Ni får sedan rätta varandras prov.
Efter det berättar ni vad vi behöver öva mer på i grupp
ytterligare några exempeluppgifter kommer under torsdag
Ni gör även individuella studieplaner för nästa vecka.
Sedan kommer vi att börja på nästa kapitel - Derivator. Vid behov kan vi återkomma till detta kapitel.
Så här blev provet i Algebra Ma3C
| Uppgift |
|---|
| Skapa ett facit
Ni ska skapa ett facit med lösningsförslag till provet i Algebra. Ni får gärna sitta två och två och tillsammans diskutera lösningar till uppgifterna. Lösningarna ska vara strukturerade och utförliga så att alla kan förstå hur ni har löst uppgiften. Skriv era namn i början av ert lösningsförslag i Google-dokumentet.
|
När ni känner er klara med detta, fundera ut vilka delar som ni tycker varit viktigast i kapitlet och vilka delar måste man kunna i kapitlet för att klara kursen. Skriv ner och lämna in!
Nästa lektion ska vi titta på era prov och ni ska själva få avgöra hur bra ni tycker att det har gått och om det är någon del ni borde träna mer på.
Speciallektion 2 - en övning på begrepp, procedurer och relevans
Övningsprov i Kunskapsmatrisen
Repetition av algebra efter provet
| Uppgift |
|---|
| Denna är fin att klura på och diskutera. |
Här finns ett gäng övningar på Khan Academy som ni kan göra. Logga in med era användare så jag ser vad ni gjort. Titta på filmen där Mikael bondestam förenklar rationella uttryck.


