Matte på öppet hus

Flashanimationer

Pythagoras
vinkelsumman

GeoGebra

cirkelns area
pythagoras
Accelerationslabben

Khan Academy

övningar
filmer att texta

Ämnesövergripande samarbete matematik engelska

exempel på film på Khan där man kan välja och editera undertexter.

Allmänt

Miniräknare? Instruktionen till Nationella provet säger att digitala hjälpmedel (dator) är tillåtet på provet.
Ma 1c.Kursplan'
Matte A kursen finns på Wikibooks.

Grovplanering

TEINF11 Matematik 1c, period 1, 2 (4 lekt/vecka)

Vi använder Libers matematikbok Matematik M1c, av Sjunnesson, Holmström, Smedhamre. Innehållsrubrikerna nedan är kapitel i boken.

Vecka	Innehåll
34-36	 Taluppfattning och aritmetik	
37-40	 Agebra och ekvationer
41-42	Geometri
43	MD+  Geometri
44	Höstlov	 
45-47	Samband och förändring	 
48-50	Sannolikhet och statistik
51-1	Jullov

Extramatte

Mål

Repetera det som hänt under veckan så att du hänger med.

Hur

Lösa alla svarta uppgifter. Prata om de svårigheter som kan ha varit.

Mål

Repetera grunder

Hur

Testerna i boken

Jobba metodiskt med ett avsnitt i taget.
Interaktiva uppgifter finns på denna sida.

Miniräknare

Vi behöver inte skaffa räknare. Allt man kan göra på räknaren gör man lika bra eller bättre på datorn och datorn har vi alltid på lektionerna.

Tidigare var miniräknaren nödvändig på nationella provet men från och med i år är det tillåtet att använda datorn på nationella provet.

Vi behöver göra vissa begränsningar av datorns kommunikationsförmåga under provet:

Nätverket stängs eller får nytt lösenord den aktuella dagen.
Du stänger skype, msn, facebook.
Du stänger ner nätverket och Bluetooth på din dator.
Du ser till att inte öppna anteckningar eller sådant som kan uppfattas som fusklappar.
Du sitter med skärmen fullt synlig och provvakten sitter bakom eleverna så det blir fullt synligt vad som görs på datorn.

Om vi gör på detta sätt har vi begränsat möjligheterna till otillåten datoranvändning på de sätt vi kan. Om vi trots detta misstänker fusk kan vi analysera datortrafiken på skolans nät.

Miniräknare i datorn:

kalkylatorn i Windows, start - program - tillbehör
WolframAlpha.org
GeoGebra
Excel
Google Docs - kalkylark
http://www.widgetbox.com/ som du ser ovan

Kapitel 1 - Taluppfattning och Aritmetik

Grovplanering: v 34-36 Taluppfattning och Aritmetik

Lektion 1 Tal, implikation och ekvivalens

Först måste vi:

dela ut böcker
reflektera över resultaten från diagnosen
gå igenom några uppgifter ur diagnosen
ge läxa.

Sid 6-11 i boken Matematuik 1C av Sjunnesson, Holmström, Smedhamre. Vi behandlar begreppen naturliga tal, heltal, rationella tal, irrationella tal och reella tal.

Sedan går vi in på begreppen implikation och ekvivalens.

Uppgift: Hitta på egna implikationer och ekvivalenser.

Implikation ==>

Tina har en tax ==> Tina har hund

Ekvivalens <==>

Vi har en täljare och en nämnare <==> Vi har en kvot

Läs: Tal och räkning i Wikibooks

Lektion 2 - Definition sats och bevis

Inledning

Har ni övat hemma?
Läs igenom Webbmatte för grundskolan om ni vill repetera.
Titta på kursplaneringen
Veckoförhör varje fredag, helt diagnostiskt?

Först: mer genomgång av diagnosen, sid 4-5.

Definition En definition är en bestämning eller avgränsning av ett språkligt uttrycks betydelse. Källa Wikipedia

Exempel: Ett udda tal slutar på 1, 3, 5, 7 eller 9.

Sats Ett bevisat påstående, en matematisk regel.

Bevis Ett bevis är en övertygande argumentationskedja som visar att en viss slutsats gäller. Wikipedia

Bevisa att medelvärdet är lika med medianen för fem på varandra följande tal.

Lektion 3 - Negativa tal

Länkar

Öva grunder i negativa tal med matteva
Wikipedia
Mikael Bondestam
Webbmatte för grundskolan om du vill repetera.
Webbmatte för gymnasiet
Kanske kan du ha nytta av att titta på denna film från matematikvideo
Lång artikel av Ingvar O Persson som undervisade mig på lärarhögskolan

Visa

20+(-5) = 15 + 5 + (-5) = 15
Alltså: 20+(-5)  = 20 - 5

20 - (-5) = 20 + 0 - (-5) = 20 + 5 + (-5)- (-5) = 20 + 5
Alltså: 20 - (-5) = 20 + 5

Vad handlar det om?

minustecken kan betyda subtraktion eller negativa tal
a+(-a) = 0 definition
a+(-b) = a-b addition
a-(-b) = a+b subtraktion
a*(-b) = -ab multiplikation
(-a)*(-b) = ab multiplikation
(-a)/b = -(a/b) division
(-a)/(-b) = a/b division

Lektion 4 - Primtal

Titta gärna på avsnitten om faktorisering och primtal för grundskolan.

Teori

Primtal är bara delbara med ett och sig själva. (positiva tal)

Alla positiva tal är uppbyggda av primtal
(man dela upp dem i faktorer som är primtal)

jämna tal är delbara med två
om siffersumman är delbar med ttre så är talet delbart med tre
om talet slutar på noll eller fem är det delbart med fem

Pröva gärna att använda Excel för att undersöka om ett tal är ett primtal.

Datorövning. Lär dig mer om ett tal genom WolframAlpha. Du ser bland annat hur talet delas upp i faktorer. Skriv bara talet på raden och klicka enter.

Datorövninga från matteva. Delbarhetsreglerna

Här kan det vara bra att känna till att:

Ett helt tal är delbart med
2, 	om sista siffran (entalet) är jämt eller 0.
3, 	om talets siffersumma är delbar med 3.
4, 	om det tal, som bildas av de två sista siffrorna är delbart med 4.
5, 	när sista siffran är 0 eller 5.
6, 	när villkoren för 2 och 3 både är uppfyllda.
7, 	när talets tiotal minus dubbla antalet av talets ental är delbart med 7.
           Ex.:392 är delbart med 7 (39-4=35)
8, 	när det tal, som bildas av de tre sista siffrorna är delbart med 8.
9, 	när talets siffersumma är delbar med 9.
10, 	när talets sista siffra är en nolla.

Denna lista kommer från denna sida

Lektion 5 - Tal i bråkform

Glöm inte att repetera med webbmatte.se men du kan även repetera på wikiskolas bråksida.

Definition

Bråket a/b har täljare a och nämnare b

Satser

Man kan förlänga bråk

Man kan förkorta bråk
Då behöver man ofta faktorisera

Vid addition och subtraktion måste bråken göras liknämniga. Minsta gemensamma nämnare.

Multiplikation av bråk

a/b * c/d = ac /  bd

Visa grafiskt: 2/3 * 1/4

Division av bråk

a/b / c/d = a/b * d/c = ad / bc

Rita 6m-repet som delas i bitar om 3/4

M Bondestam ger en förklaring av multiplikation och division med bråk.

Lektion 6 - Potenser

Satser och definitioner nedan är hämtade från Wikipedia.

Definition: Potens

I sin enklaste form definierar man potenser som resultatet av upprepad multiplikation.

Exempelvis, 4³ (utläses 4 upphöjt till 3) blir 4 · 4 · 4 = 64.

Satser: Räkneregler för potenser

Ur definitionen av potenser med positiva tal som heltalsexponent kan man härleda följande räkneregler, potenslagarna:

x^m * xⁿ = x^m+n
x^m / xⁿ = x^m-n, (x ≠ 0)
(x^m)ⁿ = x^m*n
xⁿ*yⁿ = (xy)ⁿ

Läxa till måndag att räkna klart sidan 32. Dessutom inlämningsuppgift till nästa fredag. Wolfram Alpha

Definition: Exponenten är noll

Med utgångspunkt i att potenslagarna skall gälla även när exponenten är ett negativt heltal inför man definitionerna att

a⁰ = 1 (om a ≠ 0)

Exempel: 2⁰ = 1

Definition: Exponenten är negativ

a⁻ⁿ = 1 / aⁿ (om a ≠ 0).

Exempel: 2⁻¹ = 1 / 2¹

Definition: Exponenten är ett rationellt tal

För att den tredje potenslagen ska fungera, definieras värdet av potenser med rationell exponenter

x = a ^p/q (där a > 0) är det positiva tal x som uppfyller x^q = a^p

Speciellt betecknas a^1/2 som kvadratroten ur a och a^1/3 som kubikroten ur a.

Satser: Roten ur produkter och kvoter

Lektion 7 - Positionssystemet och olika talbaser

Tisdag

Vi tittar på snittet på veckodiagnosen och delar ut dem.

Decimala talsystemet (tiosystemet) är ett positionssystem som baseras på talet 10 och därmed använder 10 olika siffror (det normala antalet fingrar), 0–9. Sedan låter man siffrans position bestämma vilken 10-potens som siffran skall multipliceras med. På detta sätt blir talet

304 = 3·10² + 0·10¹ + 4·10⁰.

CC från Wikipedia

Ett exempel från boken:

Visa att 0,375 = 3/8

Binära talsystemet

Det binära talsystemet är en representation för tal som har talbasen två. Det betyder att enbart två olika siffror används, ett och noll. Binära tal används praktiskt taget av alla datorer eftersom de använder digital elektronik och boolesk algebra (eller binär algebra som det också kallas). I Europa var Juan_Caramuel_y_Lobkowitz Caramuel först med att beskriva det binära talsystemet som han då kallade Dyadik. Medan Gottfried Leibniz gjorde det känt för en bredare publik. Talsystemet upptäcktes dock långt tidigare av den forntida matematikern Pingala.

Det binära talsystemets talföljd består bara av två siffror, 0 och 1. Nästa tal är det, av de talen som kan skrivas med ettor och nollor, som kommer näst i sifferraden. Så talen blir: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10 000 o.s.v

De gamla egyptierna använde det binära talsystemet för att skriva bråktal i decimalform. De använde dock inte ettor och nollor, utan de använde sig av en symbol kallad 'Horus öga'. Olika delar av symbolen motsvarade olika positioner på höger sida om kommatecknet. Om just den delen ritades ut motsvarade det en etta på den positionen, om den utelämnades motsvarade det en nolla.

Precis som i det decimala talsystemet är den högra siffran minst signifikant. Med enbart den siffran kan talet 0 och 1 beskrivas. För att beskriva talet 2 måste en ny siffra skrivas till vänster om den första, det vill säga '10', varpå talet 3 följer representerat som '11'. Detta fortgår på samma maner ju högre upp man behöver komma.

Exempel på hur man kan skriva för att konvertera ett binärt tal till decimaltal:

Om det binära talet är 10101101 så är det decimala talet

 1·2⁷ + 0·2⁶ + 1·2⁵ + 0·2⁴ + 1·2³ + 1·2² + 0·2¹ + 1·2⁰ =

 128 + 0 + 32 + 0 + 8 + 4 + 0 + 1 = 173

Om ett binärkomma finns närvarande så representerar siffrorna till höger om det en mot höger ökande negativ tvåpotens. Exempel:

   11,001₂ = 1·2¹ + 1·2⁰ + 0·2^-1 + 0·2^-2 + 1·2^-3 = 2 + 1 + 0 + 0,125 = 3,125₁₀

Vid representation av tal med decimaler är det dock idag mycket vanligare att använda IEEE:s flyttalsrepresentation

Horners metod

En intressant egenskap i det binära talsystemet är att en multiplikation med två erhålles genom att helt enkelt skifta alla siffror en plats åt vänster och sätta dit en nolla. Denna egenskap ger följande intressanta variant av Horners metod: För att enkelt beräkna det decimala värdet av ett binärt tal i huvudet behöver du bara läsa talet från vänster och multiplicera varje delsumma med två; om den binära siffran är en etta så addera dessutom en etta till summan. Man börjar med summan 0. Med samma exempelsträng som ovan (10101101) blir det så här:

 0·2+1=1 , 1·2=2, 2·2+1=5, 5·2=10, 10·2+1=21, 21·2+1=43, 43·2=86, 86·2+1=173

CC från Wikipedia

Omvandla binärt till decimalt

Omvandla decimalt till binärt

Hexadecimala talsystemet

Lektion 8 - Tiopotenser och prefix

Tisdag

Definition: a*10<top>n</top>, a mellan ett o tio

Gör uppg 1813, 1820

Prefix: http://sv.wikipedia.org/wiki/SI-prefix

Lektion 9 - Avrundning

Repetitionsrutan

Testet

Upptäck och visa 51

Aktivitet s 52

Lektion 10 - Sammanfattning och repetition

Fredag: Veckodiagnos.

Kapitel 2 - Algebra

Lektion 11 - Räknelagar

Lektion 12 - Algebraiska uttryck

Lektion 13 - Formler

Genomgång: Gör uppgifterna 2303, 2310 och 2312.

Lektion 14 - Förenkling av uttryck

Fredag v 37

Uppgift 2409 hade en fråga om koefficient som vi inte hittade förklarad i boken. Därför en Excelfil som förklarar och visar med hjälp av taxiexemplet.

Lektion 15 - 2.5 Faktorisering

Fredag v 38

Genomgång

15/20 =
(4x+8) / 4 =
2cd² - 6c²d =
(6a² - 18ab) / 12a

Gör någon gruppuppgift.

Uppgift 38 fr kapitel 1 i boken. Storleksordna talen utan hjälp av miniräknare eller dator: 2²⁴, 3¹⁸, 4¹⁵, 5⁶
Är det så att hälften är lika med två tredjedelar av tre fjärdedelar? Förklara på lite olika sätt. var beredda att redovisa en förklaring.

Gallup: är vi hjälpta av dessa?

http://www.matteboken.se/lektioner/matte-1

http://www.matteguiden.se/

Lektion 16 - Ekvationer

Ekvationer är ett omfattande avsnitt som vi kommer ägna mestadelen av veckan åt.

Måndag - Fredag v 39

Lektion 17 - Omskrivning av formler

Måndag v 40

Lektion 18 - Olikheter

Tisdag v 40

handuppräckning, vem har pluggat matte i helgen?
histogram för klassen
har jag gått för fort fram
titta på snittet
Åtgärder:
- alla på extramatten
- fem elever schemalagda på mattestugan (Ja det blir tre extratimmar på onsdag
- typuppgifter
- en bunt filmer och länkar

Lektion 19 - Repetition

Onsdag v 40

Prov - Kapitel 1 och 2

Provet är på fredag i vecka 40

jag rekommenderar att du löser så många "blandade uppgifter" som möjligt. jag har även ett övningsblad med facit som du kan hämta på mitt rum. Missa inte att bläddra igenom boken och plugga på alla definitioner, satser och bevis.

Filmer att repetera aritmetik med:

Filmer att repetera algebra med:

Kapitel 3 - Geometri

14 delavsnitt på två veckor?? Vi behöver mer tid.

Prov efter kapitlet?

Nåväl, vi siktar på att göra kapitel 3.1-3.2 under vecka 41 och 3.3-3.4 under vecka 42.

lektion 20 - Geometriska satser och bevis

Första delen av Kapitel 2.1: Första lektionen gjorde vi sidorna 112-117 och arbetade till och med uppgift 3122.

Vi kommer att behöva mer tid för satser och befivis och även för definitioner och begrepp, ex likformig, biskektris mm.,

Definition:

En rak vinkel är 180^o

Definition:

Två linjer är parallella om de likbenägna vinklarna är lika stora.
Alternatvinklar
Sidovinklar

Satser:

Vertiklavinklar
Likbelägna vinklar
Alternatvinklar
Sidovinklar

Övning: Titta på alla filmer om vinklar på Geogebra

Sats:

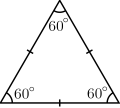
Vinkelsumman i en triangel är 180^o

Begrepp:

Likbent triangel
Liksidig triangel
Bisektris

Lektion 21 - Geometriska figurer

Kvadrat
Romb
Parallelltrapets
Triangel
Cirkel
Cirkelsektor
Prisma
Cylinder
Pyramid
Kon
Klot

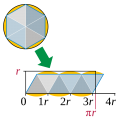
Cirkelns area

EN mycket bra GGB

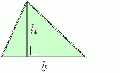
Triangelns area

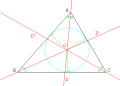
Triangelns tyngdpunkt ligger i skärningspunkten för bisektriserna. Testa på geogebra.

Arean för en triangel är basen * höjden / 2. Det gäller även om höjden faller utanför basen. Se exempel i geoGebra nedan:

<ggb_applet width="858" height="500" version="3.2" ggbBase64="UEsDBBQACAgIAKNicD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vrbcts2EH1OvgLDh04vkcSLqNhTMRk5cRzPuHVm5OahLx2QhCjEFKmQoCPlf/oL/YH8WBcXUryIsi5xbTfRC0kABHbP7h7sQhy+XMxCdEOSlMaRoxldXUMk8mKfRoGjZWzSOdJevng6DEgcEDfBaBInM8wczeqaGm/P6IunT4bpNP6EcCiGvKfkk6OxJCMaSucJwX46JYSVm3G2oCHFyfLS/UA8ljraBIcp75BTnEfzjOWDvZl/QVOWj+mJ9eYhZa/pDfVJgsLYc7Qj/Ujjd+9JwqiHQ0fr67poMR3NtPVKJzRZvHcaJ/RzHDE+XCwmJg+xS0LQf8yWIUHohvdasmsCgxFK6WcCWJm8bdgTEAxJ5oXUpzjiegoRYRBCn6jPpo5m2wasRmgwBT1sQ5ezeXGc+ONlysgMLf4kSQySGjY3wVI+WfIpBZFhQVsXXeUnMQ25GRPGQOAU4QVZgRkk1K88nKcncbhqmsc0Yq/wnGWJsLalmoTejgZrJVzgURSERLWBFt6UeNduvBhLECw59dVyLl4RArnBqziME5Rw5G0YoK6uvIoxXNJilC7G6GKEmoNPWvQbx6YYIa6uvEpT0UiKpjQ3cq1ziPGCpog3cBjBSQvlhZEdTUNZRNlF/gDecb1Slb/wezZzITrK/lHMaXytOYe9mvsMa4HTcKi+3fCnYa/x0vCaJBEJpa9F4CJZnKXSoUvB5BOPzuBRdihkMbf6H6CHbPVJkJBcfxmkEnfRW/HnWvOwlwvBZUhBZY8B1wAsjEPCyYBBHDra2y9/X+MInV68Ph1fnZ9pyMeMD+DBFZIZgchjwsuibEYS6hV4jzgTPRnCkpla2MpDQ/BSLEimbqUSADCgxRWBkOZTDHddI+eGJTBOWWkx3W+xr5Y2cvgAUqEnRPdcTgBsSIivSJapgEFzmFKEX0mggh/lnCU3kUDcDolVh8T81iE5aULyHZNG5BjfMTEabPKdThqYGN8AJAvYTlOeF+cKvfsLloBmR/txZDxDJ8ZP+Soib9JQr4Gk6ihN0ABNZrlqxCrLKEM26AvM+MWVlwI1fUvU9I16q707RQsF3lK5PfpcsrXMDnkassqJb0PMLBAzATFzd8TMh4+YpRAT5HkwYlaBmAWIWbsjZj18xEyFmLk7YhuJ6m2cpJDokjC8iufzOml19O7zNay1BTi8fAvk5TDWSkNRss4oFNsdUdzNMOAh7rCbxmHGyNiDVDu6iD1Bb7l8KvE3dFEFcq8b5H53NOA3E7ogq+KupbQt6iU2hbIkAt+DxVdceTCzbm8qUYtf47WGWr/hbmEnw7ZKuws315aGupxMUsKEawpIO8bxtmbUD7KiObAL9jA3m7G0fd2jHatsc7oX15RTAHEysDfVHJQErPhIVzbQD6OjKjZv/h/YWHtj09jczvKtrcrTz1CZDHbd8M7uF+YVUGJ7EZnTrkh58WyGIx9FeAbqvYvDZRBHQi3KT0IR1nmkIWxwp0LY5EpLjTKW918lFEcBCeWwQA7jR6oW2FUuqJZZg6dcMEesmKqVaswa1bSj31IE5ER9wI6qb47FlAT8qRAkuB9t9vamnJJyZ1pNtY0K5GMkx6Ty5JHO5iH1KCvcJuQRfw4hmKREHMg1zwWvCZnzc93L6CrBUcpP/rctIOvgk0cGficnPbh5LuA/fszwTx4Z/KstR4LfeeDOX+XvC5CxjbzrrO1uZmaubmEA9w6t2HYo8wDpqx34y4RNY9jIcLjGBGfSBG7DBN4OJvAekwk69cytAwXGceU3uHObFFFWM4crzeE1zDG6LVcp536jez7qKIE96JpVbCvQH++XCr6mKcOR1+LLowZ4b7/888En0WYIG4cm6qW2Inzrw9ud9WilxROc7qqFfGV7HdR+1TwjaNdilBC8Y1aO4ZWzs5PdVMlfqinT79oHGKRZjU1VNSaQQz8j5Qeoh8RBRLPuqss5vWsJOeBvYOflVc1hopZmumOZr8iC5X8T/PAxi9mvubAOks/ol1z+dZIzeF+rTnaf2wnEbcLecdJCak85PtJLP8sWPGerTE2VvLdDZFYgknYtASSjeRt4bvt/4H7h6fcVPIa5Gz5WBR/uvhV8ypGxBUi3/SWwBUgVotwRJfHZVAoBOSkONuU3VPyrnPzTmF3cDYJ2UG7W7TZ0qww+VoVRlcRHksTXsPdm3q6XWbg9OyzOZg17z/TQ1GXWIq5fv841uoahm6alm/2BaRv2wD7tGIM90saGpv95NdYrf2ckvtBTHy+++BdQSwcI2n+ii54GAADuKAAAUEsBAhQAFAAICAgAo2JwP9p/ooueBgAA7igAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADYBgAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

All bilder i galleriet nedan är CC Från WikiMedia Commons.

Fraktal figur

Bevis: Vinkelsumman i en triangel är 180^o

GeoGebras hemsida har ett bevis att vinkelsumman är 180^o
testa vinkelsumman i praktiken

Bevis:

Gör bevisen på sidan 116.

Läs mer:

Webbmatte om geometriska figurer

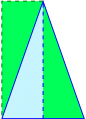
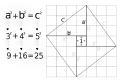
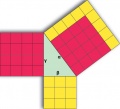
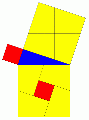
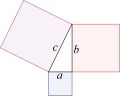
Lektion 22 - Pythagoras sats

Bevis:

Webbmatte om Pythagoras sats Fendt nr 2

Pythagoras, Walter Fendt

Även här kommer bilderna från commons.wikimedia.org

Uppgift: Titta själv igenom Geoegebras film om pythagoras sats.

Uppgift: Hitta ditt eget favoritbevis på nätet och visa för oss andra. Bra övning: Upptäck Pythagoras i GeoGebra.

Lektion 23 - Likformighet

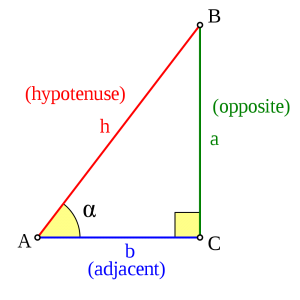
Lektion 24 - Trigonometri

GeoGebra om Sinus

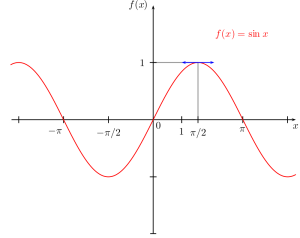
Läs mer om sinus på Wikipedia.

Engelska Wikipedia är ännu bättre på sinus.

http://www.walter-fendt.de/m14e/sincostan_e.htm Walter Fendt om trigonometri

Detta svar får du om du skriver in sine på Wolfram Alpha

Definitioner:

Motstående katet
Närliggande katet
Sin v = motstående katet / hypotenusan
Cos v = närliggande katet / hypotenusan
Tangens v = motstående katet / närliggande katet

Digitalt

Grader och radianer
Miniräknare eller dator
Datorns räknare
Excel - så här kan det se ut

Definition: Ta reda på vinkeln

Om y = roten ur x så är 'y² = x. Dessa två hänger ihop och den ena kan ses som den omvända av den andre. Detta kallas inversen, den inversa funktionen.

På samma sätt som det finns en invers funktion till kvadraten på ett tal, nämligen roten ur så finns det en invers funktion till sinus och cosinus.

Om sin v = a/h då är v = arcsin(a/h) eller sin^-1(a/h)
Om cos v = b/h då är v = arccos(b/h) eller cos^-1(b/h)
0ch på samma sätt för tangens

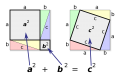
Lektion 25 - Vektorer

vad är vektorer och vad ska man ha dem till?

http://sv.wikipedia.org/wiki/Vektorgrafik

Walter om vektorer

Vad är det för likhet mellan rebubbled och bilspelet xx?

Hur räknar man på kulans väg i CS?

Fysikerna ritar pilar för kraft och hastighet men inte för area eller temperatur.

Titta på Physics.fla

Den vetgirige tar en titt på engelska och svenska wikipedia om Bezierkurvor vilka används frekvent inom datorgrafiken.

Kolla vektorerna på fysiksidan.

Vad är en vektor?

Sid 144-147.

Definition: vektor

GeoGebra: "Basic Vector Addition and Subtraction for Dummies"

Definition: motsatta vektorer

Sats: Parallella vektorer

Definition: storleken av en vektor

Mån 10.05-10.55

Addition av vektorer

Sid 148-150.

Sats: Kommutativa lagen för vektorer
<ggb_applet width="960" height="490" version="3.2" ggbBase64="UEsDBBQACAgIAGRkcD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VndcuI2FL7uPoVGndmbTsA/2JBZvDsEMl2m6aazSXPRO9kWoGIsrywTyPN0X6EvkBfrkWSDgZCGlE3T5sZYOj7S96Mj2el+WMwSNKciZzwNsN2wMKJpxGOWjgNcyNFJB394/6Y7pnxMQ0HQiIsZkQF2Gw5W7QV7/+a7bj7ht4gkOuSG0dsAS1FQjPJMUBLnE0plvZkUC5YwIpaX4e80knmARyTJVYdJMUyzQlbB0Sy+YHl129TDZQmTAzZnMRUo4VGAT51TrH7dUCFZRJIAtyxLtzgBdjxroxOaXNU74YLd8VSq8HXyhIQ0AfhXcplQhOaq1zVdIwhGKGd3FKhyVFu3qRno0iJKWMxIqmDqKUIQQrcslpMA+20HRqNsPFHMdVomW8S5iK+WuaQztPiNCg59jtNo2x3f99teu+16tofRsuyyO412y3d8y7Ns17UBbw5YYCau1+h4HcfyWxY86Dsw1nJvlx6Zzq+olIAxR2RB84rpsWBx/fcwP+NJvBIn4yyVfZLJQmh3uGWTJirAQKhQCHvpOKFlmw3yTWg0DfniyrDmmtTXy0w/oqcTjvs84QIJJRUgHpfX0Fx1jJrnKsrSMZaOKHOopKt++9TREfoamqvRlqVmaiVuuwJtW9UwLEeqAZIrU1d0aFMEGKMiZfKiugE3TddIVfynYhbCYqr7aZXSPlLKbnPLbd2tZbbjP8ffsV+3ufNQd0pFShNjzRTsUfAiN/43DtBwYhqxGdyajpJXojT/FXCY1piOBa3gmyVtWNe9Vt3+W83dZjUJNYccIEcSKhPQIhUlJI6ZvidzKFpTyQUUgBmapiTLVFmRsKQD/PH+65Sk6PxicH51PfwRo5hIeBirUW+5mGrM13QhEQn5HHp6g8Hwenj5CfVu0M35T9eXn88/g3FootSKIqRnFvHZjKQxSskMHhmmEkSB4qWzMlWwELECvOiB3DAVO8BL/VNj5YWsAnoGZplNlY6EzijUFamXhF5RK3P08Kq6cl0qt8yzdhl0r+zvt7T71SU0F5JkEwIUN6yqxi2BuLoaOuHPPH5AoxwtzKNoGeAT/ePObBU6xtQAZbd1qQSLGlR/g+/sWfjqy18XiufCIylYWfsJinCmEqg1l1Eal1uhLMsUyiClLnq1lbAmxy7J8Q7lZtNTN0AAF1uG6hkzne0YqXjcSHOTrGKywJv1T06g0KQ0h7pyusbZfFyODfBpuRRV+GUZPdoVy7FaG9X6CF7cpnud6inwanUnN4U2IkLSHMppiV/C/S9KOUQX2WrFPs3R/f+Ho72SYufbObq/4+j5QY6ev4ij94ple66Wy7OPYeltvl/a0puyXcCgW6L1jWjFjmjkcdHU/Fdsk/2SOc+RbN8SOkqVOak0sUtNHPdRUbYR0C/phiRsBm8tEZMHU39mqJ/vUB8eQH34n6Le2arwJy/C/b4zHTEChDsCDA45yw1ezVnOdjuVtf1dcx+vwg92CLs9qMLfHrnC791xraPQ6pektl9FDX9QmP4+Ye4OEubuCcLY3rfYe/Wu+ypOkxW+g3XrP0O3s326RQfpFr2Mbg+8BWyemY6i2zOPTM/W7WznNWCRCcit0JfMqG8KcBzU4W+/FFy+G9AUhcn91/JrRYru/xAoL5Ra6hvG2+9t610MMeL+z5ggHk2QuhvDbUoaJoUedlNWCePgzUH/zY27xpTevVsNy7Hqf54Wym+0N5qd+pvF/verkPOEgigVFnM8gvGLcha178L/4LXr6fgvR6OcSl3xfbOLuvajliWZXiK6TQmNfjAKH4Z79Ipwe+XpwX8ybg0YgCv827ib9U99+pt6+d+G938BUEsHCCGqX7tbBQAAnxgAAFBLAQIUABQACAgIAGRkcD8hql+7WwUAAJ8YAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAlQUAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

Subtraktion av vektorer

Sid 151-154.

Definition: Subtraktion av vektorer
<ggb_applet width="679" height="385" version="4.0" ggbBase64="UEsDBBQACAgIAGlUgT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAGlUgT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VjrjtM4FP4NT3GUnyydxo5zKWpBMCwCCVikYdFq/7mJpzVN4yh22g7icZYn4cX22E56GxaYy7KLRLEdn5zj8/n7jp0ZP9osS1iJRktVTQJyEgYgqlwVsppNgtacD7Lg0cO745lQMzFtOJyrZsnNJGDWUhaToBDTOKNRPiDZeTZgGcsGU8GTQRrRLBnllFMyCgA2Wj6o1Gu+FLrmuTjL52LJX6qcGxd4bkz9YDhcr9cnfagT1cyGs9n0ZKOLAHCZlZ4EXecBujt4aR05cxqGZPjHq5fe/UBW2vAqFwHYFFr58O6d8VpWhVrDWhZmPgmSLA1gLuRsjjnFFHMaWqMaAalFbuRKaHx1b+hyNss6cGa8svN3fA/KbToBFHIlC9FMgvAkChmlhMYkI6M4jEkAqpGiMp0t6WIOe2/jlRRr79b2XEQWgFGqnHLrET5+BBrSEO7bhviGYpMkfir0z8LIN9Q3zDext2H+deZNmbdh3oZFAaykltNSTIJzXmpEUFbnDe7edqzNRSnceroHu+zJfcxJyw9oTEKE1EPuBvftL8EfCzus95Ike1FN014xaB+SJfH3h6Q3CRn1IWk4uhySxv+QZfIVcP0avidNEu8hi6HcP/e7FDGiV4jox98KGGU2YJqxLwZM2A9JcTzslTLuxAF6bm27nTRiqa1cohHEI8t6AjFKI0mR5DGQETYpBRQDkBhYjEOSQWLbFKIUJxhEkIG1IxE4bcQZ/sdS5yyBGJ3ZpylKEggGYhBHQJykGKCQwMkSJUojtIhjiPElG55Q6yJKgCU4ijJguEaryJSgYYQv4hjDU4gIRPZlkgJNILH+CLNKTzK7dHRJIQkhIdYhihoF7cWM9hlENpukg0tWdWsOIMqXRd81qt7uBVpjOdoVPV+eDmrinXHJp6LEY+LM7iTAipdWES7QuaoM9JtI/bNZw+u5zPWZMAbf0vCer/hLbsTmGVrrPrazzVWl3zTKnKqyXVYaIFdluF2zKslen25XjYNob4LtT8R7E8leP/1iXIUz0GqB8VWje3NeFC+sxa40IJK/VeXFk0bwRa3kYRrjoTtxxqLNS1lIXr1DstooFhfoDyBXrfoDKErSfiGqKc4uNDIYNn+KRlkcwxNK0yRhyYhELMqw5Fz4KcqSE5oSmsVpSEYkRPXpnFvtUXKSjhhlYToKRzSKMdbF/lSKEeMsTAkZdZHFartBfCO2uc8aWez3X+gnqiy2SLjkT3lt2sZdHLAyNjalx9WsFI4gTtZ4KueLqdqceWZE3tfbixpHoY8/nTnQobFVFRNBZ9Que+rHzsYubGsVOpvQWYQ91WSxnScj6ixcO/Wts0Lu+qV1iZI+SxL2YaR25SwMDkTjiG/P+LaS5mU/MDJf7DK19q/b5VRs6XPoktySy/HwiF7jhWgqUXZsxo1sVau9OPeIXohcLnHoJzpAuN2s33EB/mkhZo3o1126K5mHy82G+0S99Ni5etao5Ytq9RaZcLSA8bBf5Vjnjawt32CKJ8BC7DhVSM3xACn237Pyw9Rze1AgPMZC87gopBurfA66nZqGL9yYr/BiuzCqEQ2KtzVzhXR4/vnTglfwa4mXM23kDONgDUK0rVJLscR7GRhHSMfp7dY8dhc+uwegpu+xDB5t3W6PcfqL5HQ05mU95/ZS2AFV8gvRHEDn/L1SxTGguF8uK6wJtedDLYRnkl8vdmp05/R3UNNwhzRsJkFmr+wX3dX9g7/s+9uuzdRq8qCI+6dHW4t88yB9A64nPz9chHZ4ZbeEV66WS14VULlr0DsERTXB7lzmoWUZcGLR89C0pp9ovbPOxSXwV95Zj257Y/TD62O/Q5AdEW7nalt6DV4JFvjZo91V3HQnges8l0Uh3HXwuNJoXxNz3hihsfJ5A/zUa8wbuwkgNrXF8gp8Pf35+Zr8QHk//fnhYj9e3ade3U8vqXt1JXWv/h/qHtD/VN6nl/i6qRuMZFnRAbEOvGkLv8AqOAJz+C2Y19eC2fH6doE+Poe+jjO7Ec5fB/TzXx2iFO5BCwP8PL53DWTRzU0ZTOLoNqAlfRUYfB+J/1VwP23pOrgOqJ+uBar9c+Ssw/O2CNufROEPxnS4/3ngPsC7PyU//BtQSwcI8oYesjIGAADnFgAAUEsBAhQAFAAICAgAaVSBP9Y3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICABpVIE/8oYesjIGAADnFgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMkGAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Ovanstående GGB är skapad av Håkan Elderstig fria att använda enligt Creative Commons. Den finns att laddas ner från GeoGebratube.

Vektorer i koordinatsystem

Sid 155-158.

Definition: Basvektorer

Sats: Räkneregler för vektorer

Sats: Storleken av en vektor

Fredag: Diagnos på hela kapitel 3

3.4 Vektorer och trigonometri

Sid 159-163.

GeoGebra

Länken går till min sida med GeoGebra-grejor.

Jag vill att ni ska ladda ner programmet och börja lära er det. Vi kommer att lära oss tillsammans för jag är själv ingen fena på det.

Här finns en GeoGebrafil med addition av vektorer. Lek med den och försök göra något med vektorer och trigonometri.

Kunskapskontroll kapitel 3

Tyvärr var inte resultaten på Diagnos 6 och 7 tillräckligt bra för att vi ska kunna känna oss helt klara. Ni kommer därför att få en uppgift som ni ska göra individuellt och lämna in. Ni får göra den hemma eller i skolan på er lediga tid. Det är lämpligt att ni samarbetar. Uppgiften är att du ska lämna in snygga fullständiga lösningar på diagnos 6 och 7. Detta ska vara klart senast fredagen den 11 november.

Ni kan få papper på måndag men Diagnos sex finns här och Diagnos 7 finns här om du vill börja med en gång.

Detta är en kombination av hemtenta och samarbetsövning.

Uppgiften: Du ska göra om diagnos 6 och 7. Du kan jobba hemma eller på rasterna i skolan. Du ska jobba själv men ni får gärna samarbeta. Det är inget problem om det kommer in liknade lösningar men jag accepterar inga exakta kopior.

Krav för godkänt: Minst åtta poäng på varje diagnos. Extraberöm för snygga lösningar.

Mål:

Ni ska kunna geometrin
Ni ska öva er på att samarbeta och repetera med hjälp av boken.
Ni ska upptäcka fördelarna med att plugga tillsammans

Snygga lösningar:

Skriv alla dina lösningar på rutade papper i A4-format.
Skriv ditt namn på varje blad. Skriv lösningens nummer.
Använd luftiga marginaler.
Ha luft mellan uppgifterna.
Skriv av det viktiga från uppgiften.
Använd figurer.
Förklara vilka satser och formler du använder
Redovisa dina beräkningar
Stryk under svaret eller skriv "Svar:"

Kapitel 4 - Samband och förändring

Kapitel 4 handlar om Samband och förändring och består av 14 delar.

4.1 Procent

Procentbegreppet och tre problemtyper, 174-178

måndag

Promille och ppm, 178-180

tisdag

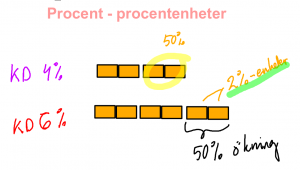
Procentenheter, 181-183

Detta gör vi på tisdagen i vecka 45.

Mikael Bondestam om skillnaden mellan procent och procentenheter.

Förändringsfaktor, 184-188

ons

Index, 189-191

fre

Kul grej: Bråk, decimal procent i GeoGebra

Ränta, 192-195

måndag

Genomgång diagnos 8

Uppg5

Börja med att som repetition göra uppgift 5 från Diagnos 8. Gör det på det krångliga sättet (elevlösning) och jämför med hur enklet det blir med hjälp av förändringsfaktorn.

Kolla: Wolfram Alpha är enastående på uppgift 10.

Genomgång:

Exempel 1 på sid 193 i boken Det lönar sig att lösa uppgiften i Excel.

4.2 Funktionsbegreppet

Vad är en funktion? 196-200

tis

Följande GeoGebrafil har jag gjort själv. Den visar tre sätt att rita parabler.

genom att mata in ordet parabel samt ange tre punkter 
genom att angen linje och en punkt (styrlinje och brännpunkt
genom att ange funktionen (inklusive start och stoppvärden = definitionsmängd)

Observera att de tre punkterna I, G, H på den blå parabeln motsvarar lösningen på Exempel 1 i boken sidan 197.

<ggb_applet width="1000" height="550" version="3.2" ggbBase64="UEsDBBQACAgIAKR9bz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjbcts2EH1uvgLDp6SJaFxJYkZKRk2cxDPuZcZpHvrQGYiEJNQUqZKQI7nTz+mX9Me6AEjdnLh1ar/YD6a0WC13z549ADl8tV6U6Eo3ramrUURiHCFd5XVhqtkoWtnpIItevXwynOl6pieNQtO6WSg7ilhMI2dfmZdPvhm28/oTUqV3+Wj0p1Fkm5WOULtstCraudY2mKeqbMGuVmtTGtVsfpz8pnPb7hZCjLNqubJ9kHxRnJu2/3ri77csjX1jrkyhG1TW+ShKBGQOnz7qxppclaOI42ChUFZGDhbBxNzqvG7MdV1Z574LXqqJLqH+C7spNUJXbpWFpSk4I9Saaw1BqbMNTzwEQ73KS1MYVbk6fYrghNAnU9g5+JIUMphrM5tDHUJmIVxe101xsWmtXqD1L7qp4UacxlJKzkUmGMFwE7TpVnAWUyaZpAkREruALdQCmcgYDCkTRGYySQSDn3xpxd9WX11oa6HCFqm1bnucZ40p9j+ftd/VZbFtzbI2lX2tlnbVeHKwzuRhGkUAZ+PKG1ezUnc2SDGf6/xyUq8vAmYshP6wWfqf+HQms9d1WTeoGUVUCHDorpNw9T4uz60X9j7Ye3QxXNDtOpHUe/jrJFxDZ00VUuvqJn3RBPe3MS1yBgjuON3D4SkxiiK0qow9778Aly53lTr/H1aLCczSPpu2Ick9hRyeHHFteKmbSpeBUBX0dVWv2kDb0DqfR6Fzs4CvYaEDRLlm/QwJBGuhZ43u8w6TGODyq3iftEfm4UmfhMuhhVxzC4oC9VhXi5t4C9M2it7//delqtDp+ZvTiw9n7yJUKOsc3AiVeqFhvqwnh+fWFqY30VZmai8ZRzDu8IblzxLFU0qVy7kCS4z7Ud+AgOxX5+N9XxeHNasKsPMFwawuXQDXnaXWRaeZtiM0WkJIPx570HvEWrQGlYoZZUwSmMgEC5FmMKqjaEBEDKZUpKBKRDJOINXrENkHCHPmBGUnRkCDgNe/IHf6OJDjOKYiBU0HHQOMOE+20GGWJSxNUp6CZlJ+N+jyerFQVYEqtYA0zkEgPF7GbUBIYcc8pIiDMWC0sv2CCqG6ADe64LRmC7KKDuXHzmHOK93CWPMdBCe3d2oPl/1WCRLEDtNOEL+6Vzu0B/BbmRIiEyo44xlsN9TjzVgM/HRdIJwTlqUebUE4bE0EC0k4NImzY7m9pV79exV82iB7ZgF7e27sXTj+9nFwnNBYYNjzuWAJAM4SFjjOYiFoCmhTyeAoIwHf/8Hxn1SjJnWpjnj+NvBc3eB5fjvPQe5NvkU6f0Ci4wOeO9p/bcP+GzHNTFdXkF3dtAitcZgKTLOEwv+UiEymkrqxwC4F6f7gXAbKRDKOnQzhrv1r8nmHjbd/LuQ12WsvcKsxazR24YggsSApxpkghDAqIzTuogAtKKUkcfEZT4EjYzjnDhJ3mIyxOwZyxx+475j587sUicgYZsD9zNF/zJ2ewriLmOEk4wmnWGKAeSzcAmMii7M0TSWncNomyf3N77vHMb/U+cLAZu56X/v3+8eBDeuwcfv1/YFz9jjAGfToUHxXdI60vS43Vb0wqjxS9z/OXqB3L9D7P2/I+/R2eZ+uKn+S34nzlxU+uR+Fd8runtrcg+y9Kvxhfl9G8W1f8yGGT9foOUpi/OzXpzDpz8IX9C1yZt9At38OAsGVk17RZ70H9+yOcM8ecEOlbhPae5J+yP30Ns66iT6EenoDt/HtuB3KwvirZIHQ8PLBXx9UGu7wvIi5zODZkDKJM5by04EI5/CYubdE7jyRUNia0zs+MZ7sP6X7t1jdC76X/wBQSwcIlJ6f5VEFAAASFAAAUEsBAhQAFAAICAgApH1vP5Sen+VRBQAAEhQAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAACLBQAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

Definitionsmängd och värdemängd, 201-203

tis

GeoGebra: jag instruerar och eleverna prövar att rita en trinangel med omskriven cirkel.

4.3 Linjära funktioner

Repetition: Förra gången stiftade vi bekantskap med en parabel som naturligtvis låter sig ritas i GeoGebra. En av kurvorna är precis den som kommer ur bokens Exempel 1 på sidan 197.

Man kan naturligtvis rita kurvan i Wolfram Alpha oxå. Det är bara att högerlicka på uttrycket i GeoGebra och kopiera till inmatningsfältet. Wolfram Alpha finns förresten som en Gadget till er som har Vistra eller 7:an.

Lutning på GeoGebra.se
taxifärd från Geogebrainstitutet
linjär funktion med glidare från Geogebrainstitutet

Här kommer en grafisk lösning till exempel 2 på sidan 206 (GeoGebra):

<ggb_applet width="818" height="449" version="3.2" ggbBase64="UEsDBBQACAgIAMhjcD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVbNbtswDD6vTyHo3sR2nCwD4hb9wxag2w7pethNtllHqy15ktwmfZ89yV5slGQnbooVa7eigw+ySYoiP36kPDtcVSW5AaW5FAkNBwElIDKZc1EktDFX+1N6eLA3K0AWkCpGrqSqmEnoaBBRK2/4wd6bmV7KW8JKZ3LJ4TahRjVAia4VsFwvAYwXX7FSo5w1K15yptaf02+QGb1VeB9zUTemc5JV+TnX3efQnVeX3JzyG56DIqXMEjoZY+T4dgnK8IyVCY0DL4kSGu0oUTSy2qVU/E4KY823zkuWQon5L8y6BEJurHbkVVdoTIjmd4BYRVY2GzoIZtBkJc85EzZPFyIaEXLLc7NM6HgS4WnAi6WFLm69ZVKqfLHWBiqy+gpKotNpMIjH22dMydprounbwWTUexBdTAUDicf3tsR2z29V7mC4WYAxmKImbAW6A7pQPO+/z/WxLPNNbWrJhTlhtWmUY8eoFTmcEop4KpvgkShKaGUhVm8J2XUqVwsP2si7vljXbosLJy1OZCkVUbZSGH3RrqlfnY2Nc2MVOJvAWbQ+rNONPnwXOQu3pn71peXCh9bmHXZJh0F3DNfECtC5JXUHh+NEQilpBDfn3QeS6XqbqbX/1FQpNlOfThuX4T9yORvukG12DUpA6SklsK6NbLTnrS+diyOHjFf46RUtIMwW6wsG4KU5FAq6uH0rericNujTdkc8G3ZB2Bg0xpoZHCmYj7G52JY32G4J/fDzxzUT5Oz89GxxMX9PSc6MNbA9VEIF2GDGkcPWaoMSo/fLZ5aIkwCNsMS03dCG52aRdHNlB+oeGKjfYVMYRC2fcAjVS4Zvg6AbCGscM30InMOPMr8PDBMIsMsaW7q2DmwJawBf/C5KUqND10G9gByomqwSuh/ZIbxuh/GdHbXBLnsfSR++C2+jPYtghbMy46Zljof4cbDTFwQ7CuJ7zfvKYAc7WO+PXwTsTFYVEzkRrEKruTDY0AiZw5nbu46wwJKcsNDC71FrTKc48v5aLw+K56bwBvgj+nhhtpOpX5eJL4tdUr88tzBbcKcduEGLbtT58veGvSHdzvETyJm9+CTw1AzHo9cm5+4g+B/ImT0g5/FTyHn8LHJ2Q8Otfzc2HrIzbtGN/5Scw/4F5/4A25/jg19QSwcILd88DF8DAABOCwAAUEsBAhQAFAAICAgAyGNwPy3fPAxfAwAATgsAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAACZAwAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

Sidorna 204-208

onsdag

4.4 Proportionalitet

Direkt efter diagnosen

Titta på denna länk

Uträkning till sista uppgiften på Diagnos 9 i Wolfram Alpha.

Sen har jag gjoret en busenkel GeoGebra om räta linjens ekvation (linjära funktioner). Den är gjord i tre steg. titta i konstruktionsprotokollet. Visa/ konstruktionsprotokoll.

<ggb_applet width="712" height="320" version="3.2" ggbBase64="UEsDBBQACAgIAGdLdT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VbBjts2ED03X0Hw2GLXkh0bWcDaoE2CdIFNc3CSQ26UNLZZU6RCUrvy/k++pD+WmaFkGw4W2QA9FD1JnBkP37w3M/LyZd8YcQc+aGcLmV9mUoCtXK3tppBdXF+8kC+vny034DZQeiXWzjcqFnJ2OZVk7/T1s1+WYevuhTIc8knDfSGj70CK0HpQddgCxGReKxPQrrpeG638/n35N1QxHB0px41tuzgmqZr6VofxOOH7WqPja32na/DCuKqQizkix7dP4KOulCnk8yxZpoWcnjnRNCPv1nn94Gyk8GNyo0owWP8q7g0IcUfeWXKtMViIoB8AuZqSbTlhCpbQVUbXWlmqkyFikBD3uo5bxDJf4G2gN1ssY5o/T9kq53y92ocIjeg/g3eY9OqKJNgPp8ULOgWEjBfOM3adnjgN3K0gRgQchOohjLRtvK4PvNLhJvzhzNHUOm3jK9XGzrPYs8HEZRcSr/KE93e7MTDYchRjC9WudP0qcTBLqT/sW/4J4yk3r5xxXngifo4Bw7NMT44hoIeojGMyjhhyUNKDP7+acgQ/y/RMSmmboA2F52PVeTZeo4MgA7GIPTpywxIXUorO6ng7HrA3dsdKKf6vrilxNk6745Ay/5dSLidnvbPcgbdgUodYFLZzXUhtmKRjHDVUusFjcgyEKBLrIwJI1ho2HkbcabISXezNTrvwzLycjCAIQ0CsVcQNgfVEqoUmOOL0FPLPf77ulBVvbl+/WX24eStFrSIF0EgYaADnJXJz2K4Br6sDUTtJl+ON3Xjv5dAbvEwcL4Yzco8qoPuR9sEV0m4VpcvHcd7jkjitmLO9c/Vw8RAXDG+TRuMevJjTqDWqxzmjN1UGZ7oIqwr5tLeuUpH3ZUI3DHme8YD2tFx4Ugt5xS9r3cNx7h5ZOodWjlvsGQshkKoDeWM7W5ScdcCd0aYacccCZefVPUaLFqvmqT50DLZZ0uOHyjTfK7P43ykz/48q0+MXM9DHeGRW4Qe5x4x7UYid+FX04jfRSDH5TkbCKY+/ejL0x0U92TZPUTV7oqqneyeQKBc0+iQKM/XAhsVPkA9fbIoJadMiX0ZXOp6TOzldZfzpHv7VXH8DUEsHCEeCl7c8AwAABwkAAFBLAQIUABQACAgIAGdLdT9Hgpe3PAMAAAcJAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAdgMAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />
Denna GGB är min egen och naturligtvis fri enligt CC som allt på denna sida.--hakan 21 november 2011 kl. 08.29 (UTC)

Direkt proportionalitet, 209-212

fre

Direkt proportionalitet är å ena sida enklare än räta linjen. Det är ett specialfall när m = 0. Det betyder att linjen går genom origo.

Å andra sidan dyker proportionaliteten upp i en mängd sammanhang i exempelvis fysiken. Här kommer ett sträcka-tid-diagram (st-diagram). Det är teoriavsnittet i boken sid 209.

Teori

<ggb_applet width="724" height="449" version="3.2" ggbBase64="UEsDBBQACAgIAMpacj8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3ZjNcts2EIDPzVNgeOjNFEjwdyo645+k9YzbeMZuDs30AJGwhIokFAC0JT9P+iR+sS4AkpKctokzOmR8Irm7XGC/Xa4Wmr5eNzW6Y1Jx0RZe4GMPsbYUFW/nhdfp26PMe338ajpnYs5mkqJbIRuqC4/4oWfkHT9+9cNULcQ9orU1ec/ZfeFp2TEPqZVktFILxrQT39JagZx2a15zKjfvZn+xUqutwvm4aFedHpyUTXXJ1fA4seutaq7P+R2vmES1KAsviWHncPeeSc1LWhdehJ0kLLzwiRJExGgXQvIH0WpjvnVe0xmrIf5rvakZQndGS5zqFowRUvyBAavQyUrRqisp9Jmou6ZVCJWixuPeRR3s3Ic792QMGh6iHUU8KPbcC9CgTjFYRkg1Agbw79p6cwqclyvB2y1LeHs6sfmZsq6secVpa5Jg+UEECN3zSi8AVJIBCsbnC5PXiAzrClldb5RmDVr/waQAw9DHaRwnKUkJToI89dDGaQjOfZLiIMRZEueYJLAz4AyUSOZHGSFJhLOIhJjE8E6vCv08i4IgysM4ilKMcepWZnfXTGtIgEJ0zcZQ55JXIzLzcKFORb0V2ejP6Ep30hYv6UU2jYUH6ZYmxJN2XrNeFgDvBSuXM7G+djklzvXNZmVfsfuZzS1zJE0hwf7n/XXmrtbGbHS0wtYGW4veh3E66oM8tBb2OnNXV3m8dVvrAw+GqAM8LMMVMgLsUj+wsSVbeB7qWq4vhweo9eU2UmP/W9fM2Fg9+y6DA7mcTp6U23TJZMvqvpghsZ3olPusduq8YiVv4NEpeiDUJOt32ICTVmwu2bBv1ykcLqvFu4X7RDydDJuwHxTstdTQ8SAebWIxHUlDNyi8Xx7/XtIWvbk8f3N9c/GzhyqqjYH5imrWMPj+tS0OW1sjphNvbIPCtrQnGLe8Qf2vhWJLitarBQWJj4dWtIEGtxud9ferqPZjpi2wswHB97oyDkx2VoxVfU/XfUGjFbi0n8deiwFiCq17243pbebmwQmsjfuUTNuw68Z9ph2SL8A5fRlwwh5OGB0SztnLgEN6OCQ5JJzzlwEn6uFE2SHhvHkZcOIeToIPCefty4CT9HDSZzfkUjQNbSvU0gYWuoTJwhLhZrJGFJufLEQDA8pR6PSgoM5V7+AzzmZIGTFSb39u0QsYEFqmYB6ItkFO/j8XO5HvJmMYtoZB6puTscV55Ips01fdw66zr4mBfWydjXIzEFvDQaTk+rPKXMPBR5kz1RDjDVtrKAFQFN6PHzuhf7rq2qWGoYSik6O3MIjUcA57/ASzCcTUCK3uqKTSiGTFtHFSs9Z3r9rl9rOiwb+3v9g3QceHQa40lfrKlCgy3OH9NMpyODVEOTGnhzC1WcgCP03yPMcgyKPEnBu2Nf5loOEeUJjqHj+VS4o+NH9+Pafw++IU4jgPMpIncRrkcRxHllOewVkJZ0GYBVke5Un6PE5kj5PmFfqgnoGIfE+IMj+JgyBMcJikcZSEmfvx8IM4zpM8IVGQhGn8X3wmu9O/PSD3f2wc/wNQSwcI5sEyAoUEAAAKEQAAUEsBAhQAFAAICAgAylpyP+bBMgKFBAAAChEAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAC/BAAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

Exempel 1

Kommer snart

Exempel 2, sid 210

<ggb_applet width="955" height="457" version="3.2" ggbBase64="UEsDBBQACAgIAOdkcj8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Zrvbts2EMA/t09BaECxAo0tkZRkoXYLOy22Yt1aIG0/7MsgS4zNWhJViUrtDnub9hX6AnmxHUlJ/pvEbrMsQOoPlkVS5N3vjkfy5P7TeZqgM1aUXGQDy+nYFmJZJGKeTQZWJU+PetbTJ/f7EyYmbFyE6FQUaSgHFulgS5VX/Mn9e/1yKj6iMNFN3nH2cWDJomIWKvOChXE5ZUyuFofVnCc8LBavxu9ZJMuBdRompaowXbzI8ko2jaM0fsnL5rarh8sTLp/xMx6zAiUiGlie71jq1ztWSB6FycCitq1L8MDCrr1WCUVE1U5FwT+JTKrmy86TcMwSUP9ELhKG0JmqJabqFBojVPJPDFBhUxaJrHxdCHkskirNSoQikdit7CJxVn7jld+kVRpu6EqF21SsdS+gBlUlg2FEUbZ8gfurLFmMAPMsFzxbsoSn+11tnj6rooTHPMyUDTQ/0AChjzyWUwDlUEDB+GSqzOo6zbiiiE8WpWQpmv/JCjGwXLtDKe25hGAv8H0XW2hhaojtdpwe9W1CXOwHLgHJgDNQ8uAZTAPq+hgHdkB68Exdhb0OdQLH953Ao9QLap7s7IRJCfxLFM5Zq+mk4HFLTN28KEciWRZp5Y/DXFaFdl1SF2krDiywdqE0HGaThNVl4DHRlEWzsZifGJMS0/WbRa4f0fKMJxo5KpQfudCgvo7NVbdRgratbN3G1i3qPlSnbb0DmqoW+jo2V+N4PDOi1Yo7jdaO3QzDS6QKbGP5ho322IFloSrj8mVzA64+W2qq2v9RpWPWOs96l841ddnvbnhbfyMGbPkfOMyW//W7W0/1Z6zIWFLPCXCQSlSlmZ0r0yVmEU/h1lTUYENl9LegiCmN2aRgjf4m4BjsutZe9f+N4n63EULPS9A5khA3gYtUTFRgkxBUBtav519mYYaev3z2/OTNi18sFIdSNVCTMWEpgzAitZNlVcoKHrXAhyqq3uvDkFU9sArJ3TbGCh0wW6+vn1oBAA0u8EQIrvk0hF8dpwl0Cwifq0rr7n4XcTN0gw+Qaj0hGuSmA4jsjMX1giHr+YJy6FLPvhWB2lhv+lzxEwPiSiSjLSTkriMZkk0k+K4jGW0hce86kiH9MXE2vWQLiX8HkMxhLS3VBr9R6A2bSxgEKgbWgw+VkI+fz1maswRh2N3GCDv2g58c+7H+epvBLrs8/zpDIkULdP65QLo85gWbSZQXIheFkp8lCUqFRPOO6VPLsW4PCQNb61JssV/bgByI3t4TfWNzGRbytdomIjRXz1Mfw07VcbEHm1zY6sJudWAFnQD7tkMdO+gFthdA6ad2XT5gOrqbvkfvgO9djsT7EbQ3I9SWlwR3HsmWlzh3YVO8FbVf/9XE7J+H+BEa4YfNKPqka6HteFtXrHRwebhdHgxXkXlUM1OXsbl8a8C9QO/6uFWqIKzhLcxeZSXO3uub47w6OS5TMlcBwy0wAsDI4cDw7QeGa2DudQAjLTAKwOjhwMjtB0ZqYP51AKMtMBeAuYcDo7cfGK2BBdcBzG2BeQDMOxyYe/uBuTUwvU59JzGV+w6bwP83hPBHCMKS+iLqi6ov959d4BJ40troZj3PKKc8mmUwnkqVtSvW9sK6/5bccTZX1iPnUMC7GDWly4TckbPJLhJpGmYxysKUKYUzptXl6mUCCu16AQ0d40RGgUo2laHpru5kB8xsiSD8zzl+99Fm6YxHvdobae2MR+25Yy8N2IfMtClN5penecIjLq923eNm+R1h1EVDvMtJNzd7xxdn+w7YxX3T/uq4WfxGRIlL9hJ3RybOvSFxm6VnRJW4dC9xt/IfuEPWPzclfbMOjFwlvbuX9FtnI9zBNyWv18jrKXm9veTdOriAvDck7np657czIVmG5t3FfqmZ4x0Hhe86XR0UvS5XbbSu2uLo7PxzEbP9FBvdYsWG64rND1JseIsVU4k+fIE/op9LWH14kqDp+dcJKx7q3KJKMsJyz9BMvWYLM9nRxcMkkeX5F52DjJk0Teo8pG6wTEaGCZdMHpCJvOqkt/5OPubm7K/ev9etxzeVpiQdSmiAaY9Q9SKeBPXxL+j5NHCpSzzq2TS4MEu50z5kzT6weXoP9pmcf6ntMGGZSJEo+ER0DOpnUF/OlCUWR+GcJRmCgjGXqMrzS6y1O3V8sLWuOmZeaa3o/7UW7gRuQAJse9T3XOLj/XLKYyESFmatmuPNBWZF70NPSN+m/qvT0xJsq/IQjm8OPd7lG9Mw18ZYJtP2Vze6VeqatwOYOHurizfV7a7+jUD/Yaf+n9WTfwFQSwcIcErZxbYGAACZJQAAUEsBAhQAFAAICAgA52RyP3BK2cW2BgAAmSUAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADwBgAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

Fler proportionaliteter, 213-215

måndag

Genomgång av Veckodiagnosen

Vi går igenom uppgift 3 och 5 från Diagnos 9. Trean kommer nedan men femman var enbart på tavlan.

Uppgift 3 löd så här:

3. Ulla lånar 180 000 för att köpa en bil. Lånet är med rak amortering på sex år och räntan är 5,6 %. Hur mycket måste Ulla betala varje månad?

Detta kan bli en mycket jobbig uppgift om man ska ge ett svar för varje månad. Det är ju 72 månader på sex år. Här får man själv göra några avgränsningar av uppgiften så att den blir rimlig.

Till att börja med kan man ju visa att man förstår att rak amortering innebär att beloppet delas upp i lika stora delar per månad.

180 000 / 6 = 30 000 kr per år
30 000 /12 = 2 500 per månad i amortering

Till detta kommer en ränta på det kvarvarande beloppet. Räntan kommer därför att sjunka månad för månad.

Här kan det räcka med att visa vad räntan blir för två eller tre månade, exempelvis efter en månad, 12 månader och 24 månader.

Excel

Om man vill kan man göra en kalkyl i Excel över lånekostnaden månad för månad.

Algebraisk lösning av uppgift 3

180 000 kr ==> Amortering 2500 per månad
ränta 5.6 % ==> förändringsfaktorn 1.056

månad     lån [tKr]        räntekostnad          att betala
 1        180              180*1.056             2500+180*1.056
 2        177.5            177.5*1.056           2500+177.5*1.056 
 3        175              175*1.056             2500+175*1.056 
 ..
 n        180-2500(n-1)    180-2500(n-1)*1.056   2500+(180-2500(n-1))*1.056

Månadskostnaden för månad nummer n är alltså 2500+(180-2500(n-1))*1.056

Intro - Önskebrunnen på Tom Tits

Beräkning av djupet

s = at²/2

Vi hjälps åt med att ta

Mätning av djupet

En annan metod är att ta ett måttband och mäta djupet. Det visade att brunnen var ungefär 5 m djup.

Teori - proportionaliteter

5x² - funktionen ovan ser ut så här i GGB. Observera att funktionen kan beskrivas med hjälp av ord, värdetabell, graf och funktion.:

<ggb_applet width="1285" height="464" version="3.2" ggbBase64="UEsDBBQACAgIADNOdT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Zrdjts2GoaPt1dBaIGi7SYekfpH7RTjptsNkDYFJpuDFt2FbNG2dmTJlaiJJ0XvJr2BHvQCOje2H0lRtkxPbI4DJfaBbFEU9b4PP/5aw6/Wywzd0LJKi3xk4YFtIZpPiyTN5yOrZrPHofXVk0+Gc1rM6aSM0awolzEbWc6AWDy9Tp988rdhtSheozgTWV6l9PXIYmVNLVStShon1YJStp0c1+s0S+Py9sXkf3TKqpE1i7OKX5BFPMtXNVOZp8vkeVqp0wvxuFWWsqfpTZrQEmXFFITbBFv85ytasnQaZyPLtW2RQkYWcYPORUhy+NVFUaZvipzx7JvSs3hCM/B/xW4zitANv+rISzPIjFCVvqHwSMLThhcCwZDW0yxN0jjnPoVGyITQ6zRhi5EV+CBgQdP5gqPzQlnatCjK5Oq2YnSJ1j/SsgCl2ONVcCvPHHlWgWTKrwWDiITE9rA8epCxuebZkFEUSm+uKGMgv0LxmlaK4rxMkxYzP3lWjYtsk7Qq0px9Ha9YXYqqd5okAWFkgYqSq7/M5xlt0gD4dEGn15NifSWJOLLol7crcYvQM5l/XWRFiUow4IHiefM9kd8iDxfa5rJFHlvkaMrghbbXcUREDvE9kd+y3tJcSmuMY+Ua2+oxaYV4AmcKEavYiAofWRaq85Q9VycQKdcbpzz/9/VyAi1lO1baIvF7KnJ4sRNJw502pMUW8SIttoYX2l3Da1rmNJNxl0OA1EVdyeCWISD8JHSaLuFUXmjAxrzS/w1GZGpC5yVV/mWDldjFVXs7tneShxdKBNdQgecpg34HuDDOhHcMDNrkyPrX3e/XcY6+ef70m6uXz761UBIznoE3tIwuKbRCJoIsr5e0TKct8LnFHw5PrJvn4rZhiD6qEB1OG/XNXVsAIMM9kQid02oRw68BVv3ELXQ/26ZFcd8ViXq2wgdIhU9o6StZAPSMlCZNh8ua9oJWUKRofa0gCAfp96DzS7JrvRV6ls7hbjVKyDK3WsgGyRrCvOJjV4sBngCpI+vTX+qCfblGP1U/y5/i3i5DRtfM2rrz/cKyj4RlH3Y17rq6RT8tj3Q1/ohdXTqNq0uC/oFEcOhutDh39DgnxhH8sNhylV7HQK+r64XJR+fj9qTfU/pdA/2err8vvb7S6xno9XW9Xk96A6XXN9Ab6Hr9nvSGSm9goDfU9QY96Y2U3tBAb7RHb9T99CQf20p/ZKAf7tIMhB/IgBqGQJSJA6w7iD6Ig7EaceboApGBjb5Al85/PoNfnx/jZLxv7PkwffnY1Z24Bk72jEqu1zGCezLi6UY8AyN7hqewWyM9zQ7Gvm7ENzCijVt4QHoauMaBLj0wkK4NYXi3iw17MhLqRkIDI9rYRgau2zHS01A3jnQjkYERbdBzBrhbI05PRtpBb8sJtg2s6OOfO7C7ldKXFbzHCjaxog2E7u5A2JMVojshBkb27DXY3dGjr+Hjh/+qSvnskjxCY/K52lUQ25f73DQXtgrQVsidTbzNbt+2Gd8VbvjXRH49bIl8r+9mD61C62bj5HY/ZvRGbqaIW+SeLd8e3GxbHwJIWoAOAHTMAZJzAEgagPp87WSATgvQBYCuOUDnHADqmxYSqDZtPJmn2/L0gKdnztM9B56KnzZbPZmf1/LzgZ9vzs87B36e4CcmyScT81tiARALzIn550DMb4hpc/OT+QUtvxD4heb8gnPgFwh+e5YEJ/MLW34R8IvM+YVnwW93rstx7lmYnIwzanFiG3hi2xxodA5AtW1ADlRfHZ3M81ds/7ZBijlSbI5UlHIGVKP9VLXU06jyd1pitXb5FVYhjxDMpPnB4QeXHzx+8Pkh4IeQHyJ+4Ch/28c8g1KtnUcIHO27EWyRTq9z0ML/3m//gL14d7288z9CjHeXdI+xacXs46dSNy8RPMa7XKfFchnnCcrjJfj4Z52LFwqE5ZS/RIRie2R5YoG7VuvbGMvIQTHhNagWqjVT+WfyKU3ZGuOZekpL537E7qmI1TszEjHm08OHBv8RAt8dsi/pmnX/iH6VJmhWpowhkJ+hu7clqlh593bK39749O/Y/nJVFqui5LgoZFgWADFNaI5SdH0TJ2XMBsf9jy2ffTTCaZEnqXzzALK/aHK/KJPjdyUM6UJTK9kPPGAR70bwwAtCz8ae7dvEtSMfN92If383cpg+6dIH3gll/HIGSCvQmdTAF0Av7v6c09KA7aE1/EG222L6hOw5XuCHdkBIGPEX0MSUwnXNuDodrtCNXIuIzSs0L+NZh+zN3du8YkZsDy3vD7L9FkTQvE+qToRJ6ISh57kEe8281yFmVN17qIp+wkPrv/54JDuJp5A2S3PAvaQJdA18FIMO5O7PG9AvckxoWdAcdHOA1+zBVXFoZ+BgVWxc9FgdYeAHYejajo9d1wvUwrc7nw7vrZwOkklRZDTeDF68T9zZzN2CYDpVI7b7IAgvZrOKMm7X9ULhz3fvZ3S8u06v9HHZbFbjJHgfPpse4uNy2OzQhP77cLjV8D4ul3LMIc6R8Xqx/eYrP1ev1j/5P1BLBwgL+X4YcgcAAIwvAABQSwECFAAUAAgICAAzTnU/C/l+GHIHAACMLwAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAKwHAAAAAA==" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

På sidan 214 finns en rosa ruta med sex olinjära funktioner. Skriv in dem i inmatningsfältet i GGB och undersök hur de ser ut.

4.5 Potensfunktioner

Sidorna, 216-217

tisdag

4.6 Exponentialfunktioner

Sidorna, 218-222

ons

<ggb_applet width="823" height="408" version="3.2" ggbBase64="UEsDBBQACAgIAKWCdj8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Zvdkps2FMevm6fQcNHZtIkXfSBgaiezJJk2M+nHzKa56EU72NbadDG4gDd2PH6cPElerJKQMGuczWJjhp3NjWIhDv/zk47kc7z0Xy5nIbhhSRrE0cCAPdMALBrF4yCaDIxFdvXcMV6+eNKfsHjChokPruJk5mcDA/eQIfoXwYsn3/XTafwR+KEc8iFgHwdGliyYAdJ5wvxxOmUsK3f7i2UQBn6y+n34Lxtl6cC48sNUXMhNvI3mi0wPHs3G74JUfzyXj5uHQfY6uAnGLAFhPBoYFDqG+N8HlmTByA8HBjFN2YMGBrLMWxd5FxZXp3ESfIqjTAzfGg/9IQu5+5fZKmQA3IirOL90xQcDkAafGEeFRF//XBLos8UoDMaBHwk3pUQ+CICPwTib8tsp5E9jwWQqyDnK2iiOk/HlKs3YDCz/Ykk8MGzSswnBNjYhJJZpYQOs8ivYIj0MHQKR5bo2dm3K6XJfhBKnRyiybIeYFGNCbYvfpa6ZPdOEfDhxTdN2bOJw21b+eHZzybKMO5oCf8lSjXuSBONiPsSHt6kXh9uueRxE2St/ni0SuUaw6pK4+AMNkAg/L6JJyFQfd340ZaPrYby8zNnh3PT71VzeIvUMJ6/iME5AIiaMuzBR7TBv5RghtBhlyjGmHKFsCKPFdegiOUK2w7zNZziIcmnKcai9hqZ+TJAC0cGNi6Wt2cilMTAMsIiC7J3+wNfU9dZTMf63xWzIQ6q8qgqTsCGT/fOdNdffCbbKKkRyzd9ehf3zyl39a5ZELMxXaMQXyCJepHkY5EtA+jNmo2DGP+YXFFhfTPqf3JG8d8wmCdP+55GdY5dXzXIU7HT3z7UIoSHlPo8yvkFxLplgInaQjEfvwPjly+drPwJv3r1+c/n+7c8GGPuZGCBCMmQzxuM1k4ssWsxYEowK4J5liKfzRy7UgzGxKA8XtcOIDS2Wu1Ox8tWdJQh8wFdWI9/J5lNfxB/Uu8qK71Vlx6W5X+OxejzUCDlW6SvfF+a5Ab6NMjZWu3OmYgbMuUkZgSVBxcaa2yytlRyGwLLkE56K7V47dMGfwHsHxvf/LeLspyU4m335HD3NP8nbb6PM2DIzSjc3y8u8Jy/z2455tx1bgbPr5J5ued1x685lfIF2l/FjWMJ3I8G7SOCjR0J2kaDHjsSrBA4/Hs1HHzxeJXgQeRxYqseipU6PCwJ+BPIh1UOjEmnVrxWaXQ0qh+mlWq9VQy/d1Uta02trvbSGXntXr9WaXkfrtWvodXb10tb0ulqvU0Ovu6vXbk0vNLVgt4ZgfteOYqc9xfoLJldRRzLcley2JxkVkmEdyZXjEprtacaFZlRHc/WLIGxPMyk04zqaK9/UIGpLs6cPEM8CP3DF6D6KveoBAondnmZ9iHi0hubKIUJcm9IeaUmzPkg8u4bmykFiuTZ0e9RpSbQ+TTynhujqaQIpxT0KaUuqizPFc2vI3nOmWK5Lexi70M3/taVfnzBcUx0HKicMNDF0rR41bRO36wEqPIB1PKgeOAg7mPRs5BBiCwfaWvnF8cNF1fGgevwQh5qwR20Csc0XlGu35QEpPMB1PKgeRraDEd/cTcelFuSxYLXjwR//6Dg4u0DPgIee6oxP/vawzxt1oWSgksDeqsBvS/VlZyiR3ohmmDeHVfS+6rcqgKdgmdsEq20lAnwq1a7yH1lEPX/7i9S3oKECGubQcH1oqPvQoIZGGoHm6VBBjiPs8XCRX4c8614hU4kY3CPYdSxsUecNxG1FCy4mnvCJJ/UnHnd/4pGa+B3CRwcNKdhZnJ1Vnx3pPjus2anfvI6GZhXQKIdG60Ozug+NKGg6wTkaGi2g2RyaXR8a7T40S0NTGdbR0OwCmsOhOfWh2d2HRhW0IsU7mppTUHM5Nbc+Naf71GxFbZtjHo3NLbBBk3ODZn1wbvfBOQpcNck9GuAampstQygYwvoMpZXOY3QVxj2pdgMcYYmjSIHgATmQtNJ5jlDnQXsy/gZAohJIkRbBA/IiaaX7IHVutKfw0ABIXAIp0gx4QJ4hrXQfpM419tQ/GgBJNscWN6SNzmNsvL6xhtbm2BKHtNF5dA1XOYTbdHNskUDa6Dy6U9UJ1tDeHFsqkDY6T7DxasEaOptjCwbSRufRNV4zWEN3c2zZQNroPLrGKwdrVMpFDiweSBudR9d8/WCNSvnHgSUEaaPz7E5QRVijcs5xaCFBWuk8vlPWEhBuopaAHkLGcdJaAiJN1BLQQ0g5TltLQFYTtQT0IBKQk9YSEG2iloAeQjpywlqCeE3W17/5r/OqwDOQp7h5S1Vrq9ZRrZu3/MtN3kLVItVi1Sp7SNnjwDf7ZibkQowdVRJa8eJlNg1G1xGXL94dLP54//zu2bvzFQMId39Efw7rTt8+5Lp3+4bic/itqQBcq5qGq7PlUzAAquSR//HN37zPqFK7WkTyLcetvyeEhkzSxJtqx76ZcQ/nyqDPy2+Dis/6vfQX/wNQSwcIVAIjF0YHAADJPgAAUEsBAhQAFAAICAgApYJ2P1QCIxdGBwAAyT4AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAACABwAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" />

4.7 Mer om grafiska lösningar

Sidorna 223-230

onsdag

Teori

<ggb_applet width="659" height="385" version="3.2" ggbBase64="UEsDBBQACAgIAHFJdz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vfbbtw2EH1OvoLQQ5G4jcyLSFHoyoGTGK1R9wLYzUMfCnBX3F3WWmkjUfau/ydfkh/rkJT2YtewXQSo0ZflamY0nDlz1ejtalGiK920pq7yiMQ4Qrqa1IWpZnnU2ekbGb09ejma6Xqmx41C07pZKJtHLKaRo3fm6OWLUTuvr5EqvchHo6/zyDadjlC7bLQq2rnWNpCnqmyBrrqVKY1q1r+O/9IT224ZQcdptezsoGSyKM5MOzwe+vuWpbEfzJUpdIPKepJHgoPl8O+jbqyZqDKPEhwoFNzK9plAYo47rxtzU1fWiW+Vl2qsS/D/3K5LjdCV47LAmoIwQq250aCUOtro0EMw0t2kNIVRlfPTmwhCCF2bws7BFsHgNm1mcwed7LVN6ropztet1Qu0+kM3NbhB4jRNMOc0IZRgJiK0DhzGZCwTyZMEJwKzFJSgFnzRLhZJyiXHacZJlrCUu7d6Ho4xw5QCTQr4SQCKNNyur861teBni9RKtwPas8YUm3C4h9P2XV1uScvaVPa9Wtqu8TnCepJHC+6LUOPcPK5mpe5pBGI415PLcb06D9CxoPpivfSveHvGs/d1WTeoySPKOQj05zicXsYZupHCXgZ7iV6HU7rhk4x6CX+OwxkCbKpgWu84GbwmeLjGtMgRQLlL7QEbnxl5FKGuMvZseICUutx66uR/6RZjKKndpNqoJF9J5ejwVsqNLnVT6TIkVgWB7equDdkbQuftKPTELOAxMHpAlAvW72BAoBZ61ujB7lCQAS7PxbvJe4s8OhyMcDa0YOvEQmMBf6zzxRW+haLLox+/fL5UFTo5+3ByfnH6Q4QKZZ2Aq6QVNI3W9aMBnAu9sgADMPLom09dbb//ieQEY/wt/BysAslfr0u90FCi1ieWhfeifSWbZlX7xnMrCjs4Af+eRIMetZwrX1lDv1hDF9rFxqv7uS72EWutauxvrlYQWuWRTGgsBGGckYQwzMHDdR5lJItpmhImgU4SDKV8E/pyiHlw8F6Y6D5M1MN0AK+zP5+AE31OOFHB4pRyyShOCZc09TgRRmmcZAkH7CRlWXI/UHu+utrf+KGi/XZg51B3FaDqKqN/YTDqPwJDVVCuvoZgTCydAtcQllqHVjLYiJag0PfjHXN8ibYOwzeQBm60r/sRfxNIW2seA4H+VAWZNnQmSLTSTIx9KDMRGNWn5fTV6jXKUbgaHSCfmED7h6ScdpXvHVuc/9/BeoRjuyBP6sVCVQWq1ALYp5WF4QDueoyM256Qwh53RVyeIwU7z6sUx7A6CEoE5jLJiPgOSSxwvCVR8rpHp7ODkuNwd3/jnUD56b8B+PiB1rGdiLv4i8QHwB3jcPzbEGxz/o6zPv3v+LvbNl6MwirjVrft2vdw12X3Dacn9Fz2nHoukbBSpqmgNKOp2yyZB48LYGTQdAUjgmRZ9rThlHyV4ZQ8J6BYFqewV8MMkomgErZwDxRMcBZnOBNMpFKS/Sx7GCi+B9Q7+Ia6RCdXuoLWmRL05XPzeLT4c0IrTWIphGQJTgWXQoaVJ+VQqpJzwimRPGP3ZtXh7k7pP736r9KjvwFQSwcIyIdjrJoEAADHDgAAUEsBAhQAFAAICAgAcUl3P8iHY6yaBAAAxw4AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADUBAAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" />

Vektorer

Vi skulle behöva repetera vektorer helt kort.

Öva matte

Khans Academy

Repetition: Övning på räta linjens ekvation:

<ggb_applet width="807" height="556" version="4.0" ggbBase64="UEsDBBQACAgIAHiidD8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAHiidD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VprcttGEv7tnKKNrUpJiURh8CLpiHZJcpyoyq9aKanspvbHEBiCMEEAAYYUmMoF9hT7a++w/3OTnGR7HgBBgpRISXa867I0A0zPdE/3148Z6PRFOY1hzvIiSpOBQTqmASzx0yBKwoEx46PjnvHi+RenIUtDNswpjNJ8SvnAcARlFAwMn5nMs/r2sd/tO8eOadHjYb/nHQemGXi0Zw2Z3TMAyiJ6lqRv6ZQVGfXZlT9mU/o69SmXjMecZ89OTm5ubjoVq06ahydhOOyURWAAipkUA0N3nuFyK5NubElumSY5+enNa7X8cZQUnCY+M0BsYRY9/+LJ6U2UBOkN3EQBHw+MHnENGLMoHOOevD4x4EQQZaiQjPk8mrMCpzYe5Z75NDMkGU3E+BPVg7jejgFBNI8Clg8Ms0O6nuu6XeLZrk0IcWwD0jxiCdfEpmZ6Ui13Oo/YjVpX9CRLxwCepvGQiiXht9/AMi0TjkRDVGNh43lqyFTvTFs1lmoc1biKxlHTHUXqKBpH0QgZ51ERDWM2MEY0LlCFUTLK0Xz1c8EXMZPy6BfL7ZMjVGQR/YrEtonbUzrH96Z5JH48/HFMve/GJkmDK89n+zG1KpaO1dudpfWgjdoVT0L6bZ6Wu2Wb3kP2adY8LWvJE1nJ//KnxdG+bZtKgiVH9dywZs3QNXdl6Dl7MGzjZ1eOpyeVq5xq74BiLGi1VjmbFsJf7D64fQF7Ai76htdFlLtA+th0LUBvAOKC4+Ij6YEn2i7YXRxwwIYeCDpig3QOt4e/nK5czAMXFxNvu+iTQJCRA64NRPqUA+hJIP0SfdSykcJ1wcVJgj2xxBK2B46HT3YPHJRRuGSXIKGNE/EZ2VtgE7DFZNIFywNPrEcc4epeT4iOS1rgmeARsSB6NXq08mak74EtduNpdUVJNuMrKvKnQdXlaVbbAqkxHi3DnopPK1HxyWlMhyzGRHElLAkwp7HwCMlolCYcapyqd2FOs3HkF1eMc5xVwAc6p68pZ+UrpC4q3pLWT5PifZ7yizSeTZMCwE9js5Y5jUmjb9VS44PdGHCaA25jwGv0uxv5pjgCs4Ih/zQvKnIaBJeCYummqMl3Sbw4zxmdZGm0uo3TE5lzTtnMj6MgosmPCFbBRegF6hRkdpcpSMQuLUiaB1eLAhEM5d9ZnmKocuxOv/EPo9xCj3hrIyIu+VT4ntNfGZGTtg15ijWb1xaiJas3H+ZR0OxfFudpHNSqkLu/oBmf5bJ2QBFysaezJIyZRIj0a0zM/mSYllcKGrZa63qRMRHZJP9hKLUOGBksF9NzqNuhaiWNEKymMiUNMS1J45IKblHQWggHmzSIXiWb3qldbZOYFZ+okAHNNFbcRkJ/YJQGzJKIv1ZP6EKRP1nuVUx4O5sOWY2g1TXJxjUX91lTSI01R8F/0kWc6P+t0b8eM05FNeJattvvdbsu/rb6vZ4C6hpE25AVcVbxBdkVqFOst4NZJKitYCb9jtn816/RbBNvHecasa65OsfaDmZMQJvBrOGqzNx4uAPO5qeGsykpzA1YJn1LAb6vAC/ajWgmd6O5Sr0V2B4DzQ9ds43GCcsTFuv4jMacpbNCpZtG6A6YH03xUQ1olVBhrh9QAPU2YGHOKsFjecxQCpOjZhOtrddyqVd5Or1M5teIhTUBTk8qKU8LP48ygTkYYk0zYUtUoSdSLImC5jyRUHDrvih9UD1cqObVZRIAH+ORAk2KRc1olsjxp5iDZnycIgquEQzfYjpOcFXMoahbebpJ80kxZoxfs5IDHaZzHPk24ei2dH0xLMgkj1HE4gDQPngs4mPKIaNFgb08nYVjOAOKspx3wFAkyEhIzWI2xSMMcAn1ZDZleeTXRqdSGFTQrNJhR2tRWBzS4QcsI9aRop/YvK4ikG6LVwCNs7GMZ1UkpwsRmhr2kqu+SQMtAamsiCCRu8dolCkQZowp/HLtt5DhctLtG+bVO5YWm06FUhJZzf4Vu+nUWJZXFAuVY4wElNSypDNejURqNb3GnZqMtmpyZ+XsK7qlRLdbog/3E324Lrr9sUUn2yT395PcX5ecfCqluy3Rg/1ED9ZFP7YeJDsrs5wV4nao4nCGLlqi5xxERzA8rJxG5kt1blgVUA/Uk1tBYKX4WeaVtrS6drNMpyGwuaP7N2N7AaWaCgsFSvi1YWIpsMjnaqLTfLtMCs7dijqvFOUfQbCvos4/G0URrSgJpI+hKcAwq1U1OigPYQBv6dsNSabKW8uEcYeOGsXBLtjfU0P3zSTNOo3jeXiSoDLkRVQ9SXS+j4KAJTpvbY8mIs/LBL4WUEbtxCPGztOS3B5QeL1gnYLqiTtAclv6lmC8h9rfjUYF4xKHtoQh+UhGGUUlC9RaS9+S1xj6FsOrjYcV3Xcs1YjVb1kS8rGargl9PDwIQVSZiMAetBxhRfHDGecNcKvHB+n8fkBfatxy+krl3Y+jcjorozii+WJd7WE4VDW0vlSiA/r15ejn0WAQHpEj8x9f/oWY3/yQibr3olE9/6wGpK5fyC4bSHayP2705a8NZnq7gDTLQjq/o+a7YqF4v+ZzZyqHH5QHZ4dHsDg4Pzxsp/PF7e5X6JXrfL7YPcjhSSKIlCXEvZSmviMCEte+RwxsHuxllnB1ljB1kjherrUp2tkVNMT3l1a4w2P7L4maU6izYjTN4siPeK3PWKDpUhxsCiaN3z4QThjLxEn8XXKd06QQX65WgbavfVcMK0193rZvuad9y8/Svva2colo+1r/W+ZtV2cBizld6LpDmBSO0bJnh5tKs1aRreauV9ruI1fakk2pRSyViOU+IpaPe45pS8jZpOBES/jlL7OUf6N+w9eglISd5vtNoouKw1hb8fF9orp7e3Ddp2oCVPZo+RmgqhAqPFeXHZzm/L2oh5WGXqIBD8xO7wjMjn24o3qtW9Rb3ku91v+pei+Uem2hXrel3tUI/yYK1IFrNcSr8L0S0S9uD+irx7aLtmpXL7k2n9s8VRyLZqiaxzjgurud2+zN5zbzfgpctBT4ch8FvvycFFiVNO6j6G+t3E/TmNFlvc/WY3XDC/+k+t9WAHL7t+pLfwEBeYBq2melsv7+A4szmLIQ6ZJEJP4oTMRnGU7jmPGndwfDUMfBUN0R6PRyUgXCr+Cg1PnxEKPitlTeukQI7wLcndFwfLvmH3QNc/tVAbnrrmBLSrFXUsp5Tp/C+/z3/8yBJcifocnwKPz7v0EekyZxNJkwyPB5eTx6qtPOhmuadr6xd8o3TRRvVnQIf/zzXzDaG+jNL3CWChSyHepW09df4x6cqsw6U5FWppKO1fG6zY+VrrracDtdp/l5026Gnd0jyfhxIsmW1C9tcNvt40PuG5QevNsDdDOs/BgV4rPWB7rX3cokoVn2p16teD1LHafc27b6Ca5WdrlFkb/owFw+sPW7FH25ssFCVwL6MnokC75LnJchw1mJUGeJyBKQpSwJn0FdAtN7Vb/O3tGoaXhidZuxXVS9n7bSFejpdpzVP3aQWHI6XXvl9bbwcdL85Cz/TEn/ye3z/wJQSwcIALqpMF4KAAAPLAAAUEsBAhQAFAAICAgAeKJ0P9Y3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAB4onQ/ALqpMF4KAAAPLAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAPUKAAAAAA==" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Den kommer från: GeoGebra.org och är naturligtvis fri att använda enligt CC.

Kapitel 5 - Sannolikhet och statistik

Kapitel 5 handlar om Sannolikhet och statistik och består av nio delar (en del har teori, exempel och uppgifter).

5.1 Hur stor är chansen?

Intro

Khan Academy om Probability

Här har jag börjat skriva undertexter (subtitles) på svenska. Det är enkelt, bara att skaffa ett konto på Universal Subtitles och sätta igång. Vi kommer att göra övningar på detta så småningom, där ni får en film var att översätta.

Sidorna 244-248

fre - hemdiagnos denna fredag.

Definition:

Sannolikheten för en händelse = antalet gynnsamma utfall / antal möjliga utfall

med P(A) menas sannolikheten för att händelse A ska inträffa.
A kan bestå av flera händelser, exempel vis att slå över tre på en tärning.

P(A eller B) = P(A) + P(B)

5.2 Oberoende händelser

Sidorna 249-251

fre

exempel 1, sid 249

<ggb_applet width="629" height="465" version="4.0" ggbBase64="UEsDBBQACAgIANpWeT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADaVnk/AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1Z3Y7buBW+zj4FoYuiBTI2/ymldhaTtLMNmt0NMGlR9I6WaJs7suiVZI8n2NfpK/QF9sV6SEoeeZxJ4kyQDrYFMuHfIQ/Pd853SMqTb3erEm1N3VhXTRMywgkyVe4KWy2myaadn6XJt8+/mSyMW5hZrdHc1SvdThPuJW0BlRkzc0bmZ4yw/IxjWZylGKdnmRZsnhI9l5glCO0a+6xyP+iVadY6N5f50qz0a5frNihetu362Xh8fX096lWNXL0YLxaz0a4pEgTbrJpp0lWewXIHk65ZEKcYk/E/vn8dlz+zVdPqKjcJ8iZs7PNvnkyubVW4a3Rti3Y5TSRTCVoau1iCTRKDTWMvtAZA1iZv7dY0MHXQDDa3q3USxHTlx5/EGir35iSosFtbmHqa4BHFHKdEMioFw5JQgMPV1lRtJ0w6peN+ucnWmuu4rq9FmBPUOlfOtF8S/fILophi9NQXJBYUCinjEI59mMWCxoLHQkQZHqfzKMqjDI8yHPa4tY2dlWaazHXZAIS2mtfgvn27aW9KE/bTddyaT56CTY19B8LMYxoxh36Mn/o/APop78EeGEkGWtt6c6LSXiXP+KerpA9RyXqVhL3HSirusVJ+ANy4h08xk4iBTlAV/oW/I42MnqAxth+mUPKvYuJk3DNl0pEDNUsv23myNavG04VlSGQ+6gkSQA2pIMgFIhkUiiIgAyICcQFNkiLpS4WYggGOGEqRlyMMBW6IFP7jKiwmkYDFfK8CSiICijgSDJFAKY6ASCjQEihKGUgIgQRM8uoJ9UswibiEFksRhz16RioCggwmQhvUU8QIYn4yUYhKJP16hHumy9RvHZakSGIkiV8QSA2EjmQG+RQxb43s4LLVetMeQJSvir7auvXeFyAN6eg268X0dJAUn0xKPTMlnBOX3pMIbXXpGREUzV3Vot6JNPYtar1e2ry5NG0Lsxr0k97q17o1uwuQbnrdQTZ3VfOmdu1LV25WVYNQ7kq837MryaBO97uGBhsM8OGAGAzIQV29V6+DEbRpDOh3ddOL66J45SVuUwMg+WNV3ryojb5aO3toxmQcjpyJ2eSlLayu/g7B6rV4XFB/AoVs1Z9AnKt+I64uLm8aiGC0+6epnceRjFKcCqwkxwQrAifXTRyCo2XEeSozQjPCFPzB3nLtyZeJUcY54VJkLGVMpjBpMERZlkmCCUkzIqJqs917SO/M3vhFbYth/VXzwpXFHopg/Uu9bjd1uDrADmpv03m1KE2IkMBrOJfzq5nbXXZpM6719mYNLRz1zxYBdQSZgQoBAl05i2WQ8RvbS+Egg4ME7mPNFvtxktEgEcpZLIMUBG/cWmco6a0kuFdjm5DPcHLAmhD50+Ti13/XcMFAVxr81CZoU9n2dRwCOtn86tZuP/uHzWpm6sNA32sg79VwXhX1A9afjO/E3uTK1JUpu1AHJ2/cponMHWyqMLldQTMOdGBp78i/wQ5ib2EWtemNKMOFLUIZRvEwio+6w1IXtVu9qrZvIUrubGAy7nc5afLarn0sohkcD1fmNt4K22g4XYrhPM9NgC/3pwjg03psgLWbdukgDCA+DeScBcyFpAMjnpqlWcFFDLUhAEMM32IfrngeWORmP0Heu+Ob0Aj2wPC9IQuRo8v1UvuLYGd+qW9MfQBIWPF7V9yFCbwQbAH3r/0C3tFrY2K4xD1DZQ0LBs4dJDJAvkG77kp/05XvYhnvuN5az8ODzB1777gM4igC9RHIXnwWZIIExHzxGACjXxGwl58XY5gfpLxHEmH0KwD2p88CLJ4QRLAAmA+0xxFiXwyx3bo2jX/C9zi8NbsWtgED0+R3P29c+8e/lnprYjVMP0QZbmG3IMfJHwZ6YNcx0g8OTDhV6/aNNxvFCEulVFhIxSWByw6XAb4zeFtzISgWhCqRSgaP7CGeH4eIHkJUu0p/OkT0MUGERypllCrFlRBw0RtAxATOhMioxFJlcME8CSH2EITYY0IIoBASp4wAPFRxIigPEOFRJgAvwTBXmIosOzGG+ENoxh8ZQhIQoFRgkaU0zRTtTsJM8SyF0MpECmHE03sR+kDq/vOxqf3L/+O5G+/v///1w45kmKTw+sI8Y4SmssvkJGU8FSngQzLGv0haz91qpasCVeGzyUtb56VJbt/xGvsLBNLEYxtx27T9QB4X65Y4cg1clW2+Rz7/9CiEiYWNKPrHbyc9u/8iTDA9ClN2mudu32ntEl49FXBwmqjeZf7Tm6/9xRaFCV+P4jPWLky1hd3BAx6iG/f3FBxDB73re3YkRL4fI/2tjwycB0FT2x067+XPe6lz6j+DZwwTSZQiwBlKMuhmnYZzDgtHSQE12i9ofq6iNU18vvmPKnZu81PIdPGbIBP1ZFISeCQEZhj7j/Eh3xBFqUwlVWlGiM9CX4dNLyKbLo7YVJzCpuL/bHoAmxgQCtIowQrjIzbRPZvIl2TTd78JNt1zNEG3JClnCisF4DLxtdh0Htn03RGbzClsMg9lk/5fZRNc25iSTHDBORcY+x8e7zucHkinmXOl0dXeKTo4DXDamKOvi5/3eD/1rvvjfN6YNtCCZoEHnH7Ij7leh8gJfW9+f+UfOsii2a//KroPsNUf0BTBc0qcBsXsEUKh2AlQrG4qMN7/nKdr5Ep7pVFjC1dHOI7QGA+/woYfQbrf85//B1BLBwiq/ZEU1wcAAGwgAABQSwECFAAUAAgICADaVnk/RczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIANpWeT+q/ZEU1wcAAGwgAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAbwgAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Kolla gärna Mikael Bondestam som förklarar kast med två tärningar = sannolikhet vid oberoende händelser:

Här kommer en bild som är lämplig att projicera och sedan rita på om man diskuterar sannolikheter vid två tärningsslag:
<ggb_applet width="540" height="413" version="4.0" ggbBase64="UEsDBBQACAgIAE9OfD8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAE9OfD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Zttc9M4EIA/w6/Y8WeaWJbkJEwKA4VyhfJyV+Bu+HLj2Eoi6lge23lj+PG3kuzUKdwdHIzmRp2melvtah/tSpppO324W+WwEVUtVXEakEEYgChSlclicRqsm/nJOHj44O50IdRCzKoE5qpaJc1pwLSkzE4DnnAxo1ycjFlITxiPRycJmdOTbB6mk4jP2WQ8CgB2tbxfqFfJStRlkoqrdClWyaVKk8YYXjZNeX843G63g87UQFWL4WIxG+zqLABcZlGfBm3lPqo7mrSlRjwKQzL84+WlVX8ii7pJilQEoF1Yywd370y3ssjUFrYya5a4ejYOYCnkYtm0jaEWKhFIKdJGbkSNU3tN43OzKgMjlhR6/I6tQX5wJ4BMbmQmqtMgHJDxaMLjKGS0LQNQlRRF0wqT1uiwUzfdSLG1enXNmMRJjVL5LNEq4fNniMIohHu6ILaIsIhjOxTavpDaIrIFswW3MsxOZ1aUWRlmZRgNYCNrOcvFaTBP8hoRymJe4fYd2nWzz4VZT9tx4z65hz7V8hMK0xDjxDLH/jC8pz8xfpgeGB47SXpWm2r9nUY7k4xG324y+hGTtDNJQvqlyYj/jZfxP8C1a/gWNwnvkUVT5tt8vrBIo++waNs/ZjBmTlycDrtMmbbJAfVSy7Y72YhVrdOFToBPdNQT4Jga8QiDnAOZYDGKAJMBCAfGsUnGEOtyBHSEAwwojEHLEQomN/gYf7CRURYDR2W6d4QpCQQNMeAUiEkpBphIYNISUzSiKME5cJykzZNIq6AxsBhbdAwM16gzckRQkOJEbKP5CCgBqieTEUQxxFofYTrT47FeOqqMIA4hJlohJjUmtE1mlB8D1d7ELS5ZlOvmCFG6yrpqo8rDXqA0Hkc3p549no4OxTvTPJmJHO+JK72TAJsk1xlhDM1V0UC3iZHtW1RJuZRpfSWaBmfV8DHZJJdJI3bnKF13to1sqor6TaWaM5WvV0UNkKo8PKxZ5aRXjw6rxgbtDbD+AO8NxL366Kt2FY7AuhZoX1V1J55k2YWWuDkakOTrIt8/rkRyXSp57MZ0aK6cqVinucxkUrzHYNVWNBfobiBzWnU3EJ3wbiGqyq72NUYw7D6ISqEgGdBJ72uMOba3QzSOBnjSHL50AqWJzj3OBpOjSTinG+J4hRtjYnPYk2QnDu4uKpn16xf1Y5VnB+eNv2dJ2awr81jAE7DSXjwqFrkwMWEyGW/i9Hqmdlc2GKjV9XZfYqu1P1sYzoBnQcQ5CrTlzJZGRi/sIBUamdBIhF10yewwTiaRkTDlzJZGCsPVLq11lHRekrAzI2tzgoXBUZ6YWNf3+rqQzWXXaGR6feOpln+1Xs3EIWKOVZKfpHI6vBVR02tRFSJvAxg3cq3Wtc3HXmxnIpUrbNqBFkiiN+sdLsD2ZmJRiW7duXmGWVxmNOzH5hfdRtV5pVYXxeYtRsKtBUyH3SqndVrJUscbzPDQvxY3MZXJOsE7I+vP0xmHrqf6bkA8jUaDubhulgq3GmNQ4EmywLl4lOCITrhcrPB5BY0JMhOnB9yPzMNNcwU1+4in2a3tuNk3HP5qwJnQTPJymejHXet8nuxFdYTD6HupstuQcA+MJ5japd3jUggbHXa9WClRncmpo6MJqdewax/p+7b8ZEv7atWe6jw7Oott763twhiykP4F1+P/Fy58TP8HYJFDYGc+AKMOgT3xARhzCOypD8C4Q2DnPgCLHQJ75gOw7paMHAD7xQdgkUNgFz4Aow6BPfcBGHMI7IUPwLhDYJc+AIsdAnvpA7DulqQOgL3yAVjkENhrH4BRh8De+ACMOQT2qw/AuENgv/kALHYI7MoHYN0tyRwAe+sDsMghsHc+AKMOgb33ARhzCOx3H4Bxh8A++AAsdgjs0Z/EB2TdPcld/GbSD2SRQ2RnfiCjDpE98QMZc4jsqR/IuENk534gix0ie+YHsu7GjF38ltIPZJFDZBd+IKMOkT33AxlziOyFH8i4Q2SXfiCLfzKyYf+PZc1foLf/TPXgL1BLBwhhk6/x7AUAAOk1AABQSwECFAAUAAgICABPTnw/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAE9OfD9hk6/x7AUAAOk1AAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAgwYAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Khan Academy

Däremot får alla gå in en kort stund på KhanAcademy på slutet av lektionen. Alla ska välja mig som coach så jag kan se hur det går. När du gör övningarna kan du klicka på Add coach längst ned på sidan. Gör det och adda mig.

Mitt ID är hakan.elderstig@gmail.com

5.3 Händelser i flera steg

Sidorna 252-255

må

Khan om oberoende händelser i flera steg:

Sedan en kul grej bara.

Rulla tärning från http://www.geogebratube.org/student/m712:

<ggb_applet width="408" height="311" version="4.0" ggbBase64="UEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAANjJhZTM0ZjBmMjFhNDI0Zjg4OWQ5ZWFjM2VhN2VkZjdcYjEucG5nAa0EUvuJUE5HDQoaCgAAAA1JSERSAAAAWwAAAFsIAgAAAJNUbs4AAAR0SURBVHja7Z3rS1RBGMbPnxWCkliW2IU+SCBkEpqgRnZBI7tJKFhaCppZimiKdlExM8vYvBVK3ipFw2QTlc17UYpsEtsjs7yOZ9fdLWLXnXmH+bA7zoF9f+e9zeHwaDi8Dfv6767h2doOa179SGblYJBO/P7Wvpnln3av9hoe/tY7Ng8KMdnth7MsykzQARrc5r8jMvxlOb28XyUQphmf320ZsvlK5En3pOn6tNJ38LqBz4sg5Yvj7ZwBX8BvxoRROQ8/muzCiquzGKbrESbyNYVNo3Pf1hyqjJW1ddza2NxO+WZjcVsiMg7Em0osTFxKWj7JUGRPMdwGCy7wkHvUGE97puTwMRNBjpBxOPQYKDpkNQBtIQLPoWBR3jvkUfZynKqPMNwQfYdYResRXKXkvxQjsBDmV1kmnESyat6LJQBz6DfQkQvzUYM2iCDxUleqm4PQSCx8KwigczHQulEGceg6KJsgcAyqzJRsNRxwDQEBZxeDkghWtSWCdCEgIHyMlOIe8WV6YdWh8aDGxKCkolUb4iG5bhJx6D2YCBNhIkyEiTARJsJEmAgTYSJMhIkwESbCRJgIE2EiO53IwOhUZXPv5eLm5Jy6jILG+w1vsGL/ta4jkUnb0tH0sl3HbrjO6NTing9WvYjAL8JO3HKLg+b1e8/97yyBIQIcZHbI8fzw1IrIs3VRF5oizz2KOFUZEn+b/oo4Up/I+OQceUdo4p2DV16Y3pM7dLUtPKWcoDzrGlaZCKKAckfYyRIP71VGnH4gtu1NKlz8vqIskc7+cQoWV+/YMq+9Ck0oEpsRZcoSQXEVRiJfeH39FmnF/9nE30RgmzBy3/nHXolEX2wWm4+cKVWWCGwTRh641OLLW9qUX5UlkpBVLSyMymj0igOJhpKrskQKql8LI/ek1Xglsj+9XmxGg68sETQXzk4koQjVxDOR3cnOOg2OyhJBZ0HtGToODziQeimJ+POME4CetcEy5DQ1Lg/11S0OZBk0LGIbjsXqn2vSbm7e/7CkuzjRoHMXXRk+yy08DsH+bFgDRgRGUtHZnHF5phWUGP8/Ewjk8xHPDwTgR372jh3xDG3StoQ6guJKIOA7uRVtOP7o+1Rxpw0mwkSYCBNhIkyEiTARJsJEmAgTYSJMhIkwESbCRJgIE/lXIqQboKqylY9jUzcgs3KQtSVW1tZJzcgobBoVX7qGZ7UlMr2wStpoRm2HleTxtCVCWnCAYBCe2NxObQU3KHVYhmwbWleUXPUU7rF+/UFpFQllg0iVZcKkkqbVIE1OoSW4QWT5p53kKJFWtMIhyyfCWRykIijLLvaOzesTL+QKpCbpJIJgIdHemOx2HaAAB/Wp+EDqeIbcpdAO5bMsgoW8Ax9EvJiJiEZFhoJ2Rb1GFocVWd4YOEBH3mC49rMmzWtwQQMT7Kce2NXaN2OSesbtl73DPRGRU1BxthNFB6DgUoonsVHTzKsfcausua1ePHbLYsiKSca7uoZ3IuQvOAGi2yeR3yCdCBCEjC//VuAP04ihAg09G34AAAAASUVORK5CYIJQSwcIT3u8qbIEAACtBAAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAAMDhiMWI4NGQxYmExNjkyMGI2MDczZGU1OTMwOTMwNTNccjQucG5nlZR7NNMLAMd3vC5j7n4sr4ZrppSMlRAW5idEM6/OQaHMo2IXaW1aHY/lGUXm5jGvbqQ7jzVFrou5siUmdkuRYR73hpFHRkrX/eP+f+8f3+/3fM/5ns+f3ywiwQ0G1YNCIBCYhzvou5vB/0hZbtfv+pOFEIiilQfo7E8dlbK+eiKcdfiyRg3RML3e8zne0lk5ycg0FQqtutWVCRX1d4WgfdDmPa/UgP6T5k/cAU2sWb2XhLiWgZEUtHYcXrWSsrYTlt4LpQOWju+lA0IhvTyqnBY5RSOoFjMdO9N2eDvP3hTVPepbWT0SH4TduVm+NNl3VbR1UanTPE8trdspfmhtXLG8rlLeCs7Focx+3N/bR6CpMBrUpROy+uWsAFTF2FiirPMYDRnU4mAN9T2N8C6XO9t1zwdb98JT+8paNzMuYihRFl78UeY18ubL6rZLyIFfUiDgdnUzQ9saQ3Zn8FM+zZlo2WGOtMxTTdtrogFtVbJlE05sunbbbmv2/n65vbxpZZMTvBoXrlLlt0yny9Ecaoj95uoUGSc9HiPRW7N/G9BqsPKEaftYN0WxdCfmssguPyt7bVEj+aZGY5dxlIhv0HxCIf2n9mHQD37QOOP7w3Ifz1i1kknO7KsrEYnrAX7T05ejDJG4YR/K54iv+mcCYUrT4yVhU9HNR+5yjmJeVszpbWiFniJAG23W6NzfXRq8LtzVSL1oqWz7azQJjHu9TnB4si/2Eoj0v4bx7/ENRObD+xXTkmfv/3acwri+tXVFjPgOtxh0MsEvMimYTBlpYEntH5dyn4Z6n6oJNXrwdjKOiJ+5F03yvzUO/9Zvn7Qx0PyHONVhvK6u0bIRa8zqxW61minZIgvh8ZtuPX/9AFcriBQTxi7G9ZFfCMMGyDMkxaIiBXIxwVNgkC/7OuiBmBqcWxB1p7bFHmBjSabzD/c54TcyuxK5N6pyayzCK5ur67OUVd4Zpz7jEAyXBFiTYdZyeO6CDAFFofC7yzDyAsV+ImqWpV8f4gyC7rvYaxnqTQT7689qjJP1RMN7QJDBWARop/0GktorWBc+b6qHYi6pyXzgAKDx2E0hWHsBcRr6tI+qANO9wMba/sudqB4w3C7mTXOaPFyfs+L/IQOFKxlS9sS8uUeTGKiA6fdSBCVTr0yEOE0jozGQOOqNrBUviFp4oemhgg06fU4fRHIYdmwUGgEDvAq89ALU3K8qKh2yXlYoYxKtQDbSBntyaNTIHT+kea4RHfYgrO1DnU7gMvNlXEP4twbBAZXY7MyY54AKLTuTa1GxB3AFAR8Q8d8jn4FGBfcMzfE1ccA7VF6ZnnchSMqxTYhzGILnm0sEA5sld+iAG4Y/ItCKn7lBz40B3Jb+T0Fbd6SvKulEPS04KHHvoe7MwnQsHMOxLQx/wE2YF3UUXhlzYjQxFrYtMVy0eR1Qh8pDIgcHG9cK954qvRRbtU4tdUzmH5YIeCtEjK3TK+XBnGGNHFrnz9m2CSQHkl3HJ1zgyyuuva/PSwxuMw25hi/Y3ZVsoDiWPBzh4fkQf+xYIIZ3FMVjLhfmaUSaVMV9/KBZdcioDyWoPXsGqUso+4R/5PQOPZIVxiEOi1Mk1WCyHHKmViIfwRdRLW4GUcV95zl3KJPywRZJqH6fqaqus5wCtHkHVN2MnhQ+CdHvSNFaGpxPCElTRd6jDv6ZQzNfT1zwxbl8aaeA+7pjoJSy3IJqeSI9IruWdL/NLiBAF8udS9+SDJV4py9yClemHp0jMNYV9ztRtwtnbAhmWspFt5idezZVzUaFxW384zq7NwrxcCWADfiw1L8BUEsHCGQ+JSdMBQAAbQUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADE3MDY0YWZkMDI2YWRjYTYwNDRjMzRkOWU2YzRjYTUyXHI1LnBuZ32UeTjUCRjHR65xDMYxzahh52eUYyZH5Ejl+DFkhkljne0sIYSKYTCVyoQh5cq4jxxt27htYSjPSI4YlUiIIoasPI4c69jl2d3/9tk/3u/3eT7v93n/+74ssgMBJqksCYFAYHa2oNOue+wNdN+uplNC+BCIKMMOtKBEDs/nb9pTLBQ7FqhKmWUbHFK7pS4GGi2naCFq/Tq2NSHxLadVxQmbhvBesRSp07fHO70Au09rp7t2bxUnD2GfVN3JK+fOXePQI/hjLW1b1YwWxkKPIM8kzE8mzMA7Yqpvwb/hIeNBWVT99LvXxcIB7m92Ht1dnemhj+woI2I2h8fFJR21tFWq8MskUXTRzayP8OwoQ7OGmKpC86zAhfJkapOKsfpSTcXAyiabEWExVy4ubt7NmljUfC1aj1LKVza53vNOx5PlgmhbYUgrbBhV9Q1sS8afv65ZlwoFN2lW93FBnp4pCXeEJ3sdcUTPl0cGX5F9SHryMoitVt7qeglxrEVNVvUofAiKIuCOSh5CfzWEbBNEcqxi29eGMWy6i7L/KhxtxBzHVPK+21Y9epHeBcWBax25ygKWtIsqnA3BZUaJqjTOnJwuMgF0m7/c98u5RZ4df2Itd0Pg3RquJjWxBS8UEysw+okbs/6pFz1yaWF8jfNZv7LHpmQ2hKR7WTonu2vInT0rq+Dy3qWA7y5P1clgvtyM/o0WkCp/KxAKdeUifcDLA6vsyIvn+EtM418iDlY4lNVGApgsKSGhto7ImjDu+tLycileJvpDtq9b8kZjRfvttUFOiIfzEKV6KSgCsa3kdBomI6sO3mVZ2LQPwyTutRTTqZ1d33DaehU5Td32lVNTTsdtvo3bC+2lDu7Aa9yhYElpNjs004NTmyu1/CJYkCQJjD/TzNNvyUw5DlziqqZrTIzj38dP+X7XzmTlYqyc7Q1F5UMJIuUeZvuH/bko4TLnYBLFthMNXyGZrQz+CngA82WYK2FtTaHW4N88eCyEHZf3+4c3M84geJs5Cm98Fl4XOZNPrgmWKnppQFOCn8Fg6KDKwEDi4TGNnqfXtufJNQ2obyUAoIX9chdafmSR7Ko5pDWH8Ox9BTeK/ZdP43O29ArdmlWEcymUj8qEvdMWqKaBQwUeXJoEh86jW8XroRNHqmecBAWPUlIuAhrBXPqb/gOhLq3UOKrG9NWrmWgQV5NhytHCZkjDaWlEZWeDTpqoGM6QsW/stAYKcMjM9S8LnCdji7+wEvASrppZIdHa7oNRSyJ5c+8WlKLUi63hn380S02pSojkbhyUk0gQAfcBAQ5MRyzxFDwkVbcXRNrwaPJeSIl+O6YXlngYHrcHG6x5KwqfERL9jkyPf5Lb/wURJ7Uf2yLZ4bBdlQJGAS/PVcI6yEPOF9ckMkU3OUKpN2zNsT/wkqFPFQhJlxyXwIZ2t+ZAx7Q9Nwty1N9zWkEVazGpzv8ktQ3Pf/DnVdhT46SdZcPRCdwffe8vJ9XNnPr/xepV2BSsmh/UjudPRDF2pmBIU1qrV4hEyBWE7MjRAyzyMbXJ742mi+qj/cGPH3MmcCpPBAKBXXeyH7He4Gx0c7tO61nVC4ulJzKkZOSkecu7fW1rpu7mCurjiR3sSvGwxsrOBlPi6GTd0vmtE9nOyAwTYJKUXI4LQDlrHH7YqW5MwJou5789w+P4KMqYXAMy1G3cRKbqk6ibm/oXmlO0yMe6ogAkLqN+zc7X+pC5kMzS2cWbtZOoWrYlfX2s27s6JeJTLFLHD+CdSS1uPXclDYtvkURoh0af/wRBb4ipjRUaTjWL7TfWnS3o27+d89XfqCw6bt133pYIDin2GEupW4sXrXQrOnbZkMLrpym8nhyp6aSOj6H6PoVld+65wBhAqY6rEG/kIfZ5gLueua5P3pbHzef8rLcowYBszO43hthZO4CVlj/f+gtQSwcIm4KhdKcFAAC0BQAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAANzcwOGVkZjA5MmMyMWM5YzRmMjRjMmQ5NzkyMzI0MTlccjYucG5nlVT5UxIIFGa9QlFLSTGPJDKPMlPbQm0bLzoQ82RHVDwyLC0PsDLzKtlSEExJrEg0RSVpVUwoUnPNvFBRwmO8MguVcTex8Danddndv6Af3vvmvfnm+968mffIfj5ndLSMtQAAgA7yLCJAiaH/BlBFmQvRCQMAgLobEuGOTpmQl3xH7XY36l7n6g8Npvc0oW1VQHfKIERYdRmwBphbPd+v3XAfQasBegYirFFp/hRtTkH4C0daxbC5Cxkl/dYrHOLfEDQvnpwckPfbu76v5YlF6TLGpVLnlL15j8I2vx8yzhyGJ7dEz4o4n34biQ1x+Ju8WDcv4svTdSitGSamgLs5RZ9TR+k72ETdd5EMyBmcbKQPsrWuoXmHs5Y44TR+VWxDE9cKvL+4TvNAIfDVKGAl07rURb3ptkNFVAA33/xoP8hXWtRp35IfD2tdZr+UXXIyBXkxKIh6fv7vx4WUvBwkWehUP03seNsxN1VFcdwdHEi9U6x+BDNWGklXnJAvrTmAs/IKCB2OFR/flQervnNFlDnzg1W4Zkmb+BelPuYOBM8NM6kNNn/FxQuju79+15B5fEIIdGlJeF4BfBPFCPpIo/w5o/3YSqUdFR7LtgEWtcWHqv2UYqeBhTdAB06l7zFOnRgeuzn/pt9scnLtS1rALXVfGUtyTWA55qRRIsLF1fYNP32evVr0lMeTXgmLjblWdsvf8xOsmGVanX37djPF/bSab/w0gnvsJgosLZvIWCEVluNp0TTVq/ugkVtG4uQESMTF1nuT0rKBgTkc3EA2fdBmEdPy7Ho04apkablxfCWoZnB7X98rj9lHRjh0zVTB12bB8I2w8MWppYChWs5TFv859EmXoonXfqWBesjCZLQVUWOnIrGOlc29rjIULDyQqkgW3uayhOtfPtCisfvgiA/rq4MBHeuHR7cM5iAP50hdGM98oWNdAQpmP+Vhx5esdRtZxzuGzcH6DnSf1BOdA7a0JN09TKtrKIjBtr58u78Bm/Qe3PbecCE5WNiTmMxPO/kfk3YlFA4ql5frT+q55cV+TkU8QN1Lg+28PKBFhueC4psTQUWkLrz5/2Q90zAP65rdcUWrQGOtJcQF/ArJ9qHpOgKfIPmUvyxipcXFBUhSdj6m/Nf1y04UaDVeeohrS7VaMHGhzvj93F7Vd0I5SACMONiUBkFyxREat/ZkljstK4KTdxE6vWS6zwui6YX6et73vY1/1RauqGmIUo9hhI69BN+OnuvgCr68WCnORJNJTywiqyKbOEHUhcUeML6uBIQsseUy6SS8gaHSgQ5lyfLFj0mWLHIM7Afg7Gl9fwu7bH/lDrw6O+17CUjEi1dGXRvGcASaQlEc/cOSHY6lihXHnnV2bphHVIRgqds/UqSYRHjeVK05GsoxhLTvjViGJ7752nY5p/GAUv08lau8IutimoL98nS6putfPEtWCFb7Qnr/wiihN+8iNSyxfCWFsw39uj0ThZn1s3NysweKZ57p6C5n2hhA2mE53t04ccsmNgiHNbNc1MRsOnyjiQ5q9/5Ck8gsAx/wqQfphYGz+kwr/RIG+xrd/tCeu54+T4DRZH9Dd2e5VNCWJRo/UqlFP5eUBTwOOiDPwDTagcsAOzY5G27jCu1xVLlhlqBhzLbSbAO6RmGQ8GicNT6IaYFEcYl9ucwPRk5uZxIiO7Z4bOboR5UdllPLm1Hh4KkwNlqMyQw+oQ/WO65u5dNQOQ+ghzOkNuPVnHtM5yJ73sXBdEXMYStPXUzvRspIvZXHN6IJ9HWG11Ix28BELbSrp9VgQ5UQPcKIK7ivqXypAOQpH0SdRyTxH1BLBwjNms5SVgUAAHkFAABQSwMEFAAICAgA9n15PwAAAAAAAAAAAAAAACcAAAA5OTBjMDdhMWJkYTFlOTlhOTMyNGQ0ZTlmOGZjZTc4MVxiMi5wbmcBAwX8+olQTkcNChoKAAAADUlIRFIAAABbAAAAWwgCAAAAk1RuzgAABMpJREFUeNrtnftLVEEUx++fFYJSWJbYg36QQMgkNEGN7IFG9pJQsLRc0MxSRFO0h4qZWcbmq1DyVSkaJiYq5iuLVESX2L7LLGfHu+veq+0FZ3aG+WH3eq94PvfMOWcGzlfNaTTWHX87Bmer28Zza4cyyvsFnfj7m3uml5bXDe3V/Pyse2QeFKKzWo9l2qWZoAM0eM3bIzL4fSmttFcmELoZl9dpH5gxS+R554Tu+dTij/C6vm+LIGXG8XbPgC/gb8aEUdlPvujswhVvZ9F0z2OZ8M/YGobnfq05ZRkraw682picdv5l4+KWRHgcWG8ysdBxKWr6ykPhPUXzuVjwgJ/YI8d40TXJLx89EcQIHoczOAaSDlkNQJuIwHNosUjvHfwoeTNK2YcZrrG6g11F6SFWKglIMgILZn6FfcxNJLPqE7sEYM7gG6jImfnIQS4iCLxUlQabg9BIsH1gBFC5aCjdKIKY/xV9w5Pljd3XChuTsmvS8+sf1b3HlfUNh+jRBAtHo8xMwdb/mJj5eSKtZM/J294zKqWw6/O4iETgGgwC9i4aBRFcNXwSfhF2+q5PHDRvPXwlnLMgXDAIWD5acmEX+zK1sGqIg8wOOZW3L6Us4kJN5OWGiItPw8+Wh8Tdo59iHQnnJlSYaBRU/JchoxNz5B2hCfePXH+t2zUdvdGyL7mUoLzsGBQ0uHqI+EvaGw6KHWFnivzsssPPPWa3HUi0Lf5ekZZIe+8oLRZv79g0b74NjS9gN2OVSUsEyZUZiXhheBiDsCJiNNkeEdjGjDx46Zkhkagrjezm4+eLpSUC25iRh682mTmzo/gqLZH4zEpmYWR6vSEOBBoKrtISya98x4zcn1plSORQWi27GQW+tERQXLgrkfgCZBP/RPYmufM0OEpLBJUFlWeoOPzgQOilICLWHmd7RDDq7ANuU2NzkV994kCUQcHCbsO2WOaa1X3yeMfz/sMSH2BHg8qdVWX4zJfw2ASLVbDukAiMpKTjmbG5uitIMSKeCeyEiJkDAfiRcN7xv0TYoRHyCJIrgYDv5JS1YPsjwcHiTojIfdSqiCgiiogioogoIoqIIqKIKCKKiCKiiCgiiogioogoIoqIIqKIKCKKiCKiiCgiiogioogoIorIrhqB6n2SgUhge5+EJxLw3iexiVjR+yQwEYt6n0QlYl3vk6hErOt9EpWIdb1PohKxrvdJVCLW9T6JSsS63idRiVjX+yQqEet6n0QlYl3vk4cI6QaIomxlUe+TRzcgo7zfvLbELhkB731aWXOQmpFmaxhmXzoGZ0UhEvDep6mFVdJG06rbxkkeT6YDgW31PpEWHCBohCcmp1043a9A9T5R6LAPzLi0rii4mhTukWyM//hDYRUBxUWkwj6mU0kLqkGanExL0EVkaXmd5CgRVoIKBy+fCGdxkoogL7vYPTIfPOuFXIHUJN1EsFhItDc6qzUYoAAH1an4QOp4Gl+l0B3SR1ksFvIOfGDrRU+EFSo8FJQrAhWyJgc2K7y8MXCADn+D5l3P6jSvwQUFjOh6vrCruWdaJ/WM1897h28iLKYg42wlig5AYinFk9iobubWDvlU1txSLx5382LIkknGe7uGMRHyF+wAUe2TyK+gEwsES8bMvxX4B9An0jII7Bk6AAAAAElFTkSuQmCCUEsHCLLR8sMIBQAAAwUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADg5ZjJhN2JkMTgyMTM5NTJlMDI0YTZjNGViYjM0NjhhXGIzLnBuZwFMBbP6iVBORw0KGgoAAAANSUhEUgAAAFsAAABbCAIAAACTVG7OAAAFE0lEQVR42u2d+0sUURTH588KIUksK+xBP0gg9CCsoAfZA43eEgWWlkJm9iC0RHuomL1jK61QSrPa0DDZxMKszCIVsSW2r9zl7HV2nRl1hvvYudwfdscZ8Xzm3HPOvV84GhG7MRH+1xIcrHkaKqp7v7/ytaITf/+9V1+GRyZs7TUsftbW/R0Uso49WVkQ0GaCDtDgNc+MSPDTcN6ldp1AmOb64meBzgGnRG4+6zM9n1vxEl7X8XEIpJw4njwDvoC/GRNGHb/2zmQXrsQ7i2F6HsuEf6a0sevbr/GILmN0PIxXm13YzL9sXJyWCI8D600nFiYu5Xc+8FB4TzESLhY8YBF79Bi3Wvv55WMmghjB44gkx0DSIasBaAoReA4tFu29gx8XH/RQ9mGGG6zuYFdReqiVSlxJRmDBzK8K9EaJFFS/YZcALJJ8AxU5Mx85aJIIAi9VpcnmIDQ2lr5gBFC5GCjdKII4/xUdXf2VTW0Hy5q2HK/NL2m4UP8cVyb+hlWPJlg4BmVmCrbWo2/g5+q8i/PWnIifmdvKWt+GVCQC12AQsHcxKIjgqu2T8IvUDacS4qB59Pxd5ZwF4YJBwPIxtpa1si+ff4zZ4iCzU9YVp227nLGrdunexozd19O3V6asP00/xTpSzk2oMDEoqFiXIT1938g75m88u/zQfdOuacXhh2lbLxGU2y1BRYNrjIhV0v4bptiRuqncYpedvuMKu23R5tKh36PaEmlu76HFEu8dU+aRR/NzzrCbscq0JYLkyoxEvLA9jEFYUTGazIwIbGNGLt5zw5ZI5r4mdvOqnRXaEoFtzMhlB+44ObOj+KotkZyCq8zCpfkNtjgQaCi4akuk5OpjZuTC3GpbIkvy6tjNKPC1JYLiIlqJ5JxBNrEmsmBLNE+Do7ZEUFlQeYaKwwIHQi8FEbX2ODMjglEf6IyaurYI+TUhDkQZFCzsNmyLda5ZoyePJ2PvP3XzOexoULmzqgyf+RIem2C1CtZZEoGRlHRic22R6QpSjIpnArMh4uRAAH6knHfMlQg7NEIeQXIlEPCdwssPsf3R4GBxNkT0Pmr1ifhEfCI+EZ+IZkTkUcLEE5FNCRNMREIlTCQROZUwYUSkVcLEEJFZCRNDRGYlTAwRmZUwMURkVsLEEJFZCRNDRGYlTAwRmZUwMURkVsLEEJFZCRNWs0qrhInc18iphIkkIqcSJv58RDYlTIozNKmUMP+c1SfiE/GJ+ER8ItZj7rqPPkTc0n00IeKi7qMDEXd1H+WJuK77qE3EC91HbSJe6D5qE/FC91GbiBe6j9pEvNB91Cbihe6jNhEvdB+1iXih+6hNxAvdJ0aE+gao1dnKdd0n1jdgf+Vr570lpBou6j6j42HqZmSUNnaxLy3BQbWIuKj7fP4xRr3RjJqnIWqPp9+BgEPdh3rBAYJBeLILmxXt+zV33YdCR6BzYLLXFQVXh417NBuhr38orCKgTBKpCvSauqQl1aCenKyX4CSR4ZEJakeJsJJUOPj2iXCWCHUR5NsutnV/T571Qq5A3SSjRLBYqGlv1rEnyQAFOKhOxQfqjmfwVQrdoX2UxWIh78AHtl7MRFihwkNBuaJcIWs7sFnh2xsDB+jwNxjx9ayp5zW4oIBRvZ8v7Lr36oup1TNeP+8diYmwmIKMM11TdABSq1M8NRs1zaK69wk7a07bLx53882QNWsZH+8a9kTIX7ADRLVPTX4VnVggWDJO/q3Af6WXA3GFz2jzAAAAAElFTkSuQmCCUEsHCKCHXJFRBQAATAUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADk5ZmIwYzI3ZmFjNDM0Y2Q0M2Y0ZDU3MDY0NTUzMjJiXGI0LnBuZ+sM8HPn5ZLiYmBg4PX0cAkC0tEgzMEEJCeH5J1jYGA193RxDKm49Xbub+8QR5Hj7+eLNk2KmHajuW6CwgvHiCaxm8zd94RYp9mynJ3XsiyFX3hzec5SUa+fK3h4hYVFTxt1G6VEJ/3W2yyzfPfr2jf3blpXl7f9TPz+7o618fziZ2dmcj9fI2ai/e/A/W33zofP45tqvu928OW5S0Qf7/+elfNq+v2SfbMO5sv+jXdQfP9h8tOldudDLjBKddyUm3ivP1hV3Hovi1P4ddn6Z68lt3s9ObY58e7fo+nxTq932fk0TRE9Onm5g7hBWojPqxNXt++qfOi1ZFPGrt8bfX5Ua836rbbvPMveoGXpTAJvV20Ki7uxw0JdUI792uzpES92hNyvPO/80NS1e1dEQXPj249uO6/aHdKXtxW8wSHnbmDKZSY7y5ThrzvLLOfuo59vHZzOzc+W8T1R+PqM+wfXHfrqsW7tkYlnOXRufMmubU5UWvp1/U1VBu5lcY3u55b122q4sLRN33MpJFhAS1orzoDpQ4zJjrwUxzX2i1bnL1m2NDk+1PvhxLa5y2edu1/Tp/3PvjFlu1qEhdTbMyk5vac//Ng+VVX82Vo7qchi89Ct+yWLUr0KvThWHVR48GbRRMGDoZetL2Yf+yUcWBhgW/IuT2nqUUHOgzEGHBF2UYGh1r+Nfn3drsn3Sif37cczvtM3bTd98ibr3L063exi31u7Jn/RXjJFQobPq0NGuLena6O0kYGNY+3yfIu9Jf9r767MvNnYPtNVPFNm++0q4YbDjpyC7ZFKbrO/zWfITDt2LKs5uOzatNNrbh5q6jopf/lRgYWeYrVLlDW7h8jE2v/h/HZe59en9Co6B+ZNZeC8qcx0+ew87lyTWknmpaK5vi4eJ+QEz/Tallzse73Mpah8+4Zj2tvmibq4tLS8ETx454bz9Dd7k5/OlV0b5+gCUjvxzyWrbxfmzPVdptwgdfkSVKFl6PcZtoWOhXszv3d7S0Um7+hv6uiYMMFW6cauQ79j6lRzpn7keCbeVs5YIAI1eZ/rbPtvxs3vNm7wdD06txDsjCmz9837EHJ9yuEq97fSVj1vJ5geXug9p1rNyWlbZ8s9G7nZtVVuByV/nP7AfXNe//k9zR3K0wLaQ1takhSbPCd5zl6bfao0POGA0Ge/A5GcR52OnCoUXiyyVrZJRcRa8JsXUxjXstlVR0+c0rNtKZ77o9zVz1NDT2mTqLvKE02lc/tqwlxEBF1dBANJoIImdeQIun/sVy9T2uQqY2k6T6LzhFjhkwcVSYpK0Ucmzv5o6vhTqS+mb/1E3Ucn/v6QuqnUd6efBI5HTg3vU16DczmqoUcmdnw884z3RvDlXMPtLSGC7uf60qvUHG72bOl6Zvdt6drvm1eu8xIF2e22/9+yOxm3pi53niKn/4+5Qkm5T0aG/2kTM0vvhzVa2VtnfPde1aHsfsx52eHrxnKnSl2PXU16JNc/daG//ck1hxa0dFz5xVYaeSloVYCf3zRvA5eUV9PnXwo8tGaJCJ9drdIUVY9Ilp9buoGlQlD63glaAWYnDQR1xLxuzS7/4anlwMj3Kfhj46bHmXumO+na5KdujPCw/tC4VtxW8NmKDwEP1kV4TpoWw9ouarfXsKCB775D95f0Usv1B1n5fDY9/3x0z7u9UpeXVrX9qHzb4ddyU+SNRbGqK/uCJ6dE/E+6lW7d8zH2yplZxc+63bPtJDcdDzrmvqrNUvCS+ByGh2+DJ91XWRuhEGEU9i/sgfwiM5OFk2P0TYElKYOnq5/LOqeEJgBQSwcIsyYwX0oFAABwBQAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAAYjMxNjQ3MzhlN2Q2YjgwYzc1NWEzMzEzMDRkZTNmMzVcYjUucG5nfVR7PBMIHJ8Vx7BsiKldbmbovDqUV55bbcirYaKRUHqseV1kIc/Z8lh6eA4V1ZHXYh6xQyimxTqEiFCuWTmaOOPm7v68z/3x+31/n+/v+3v88/tluLseVQRpgAAAgCIOi/aUoN+2yQIlPhdPegkASMfj0Pb4mLHF4j+d8fYqvZ9LVO09VyrUxErXXiXXJv105S6jDQnS/zG1Sh8jsHdTNIlT9wtLHervqzU+8Mi4v14XE5Wx2MqNKBJWr9ZNvrGIWwUvdwm/CttMSiLnufkW3EHq6C3Gl6l5Ubv8rhb6+UkVPAfLp4mmrqzHvuNRLyYo0jkN7WIZkLNoKgCv/scxaXjptby3kLAt4xyfNa6bpkv03HR6WSPxAbraRnBAHH98Tfns2+XVKfu+jJklvVfST2CqxZbkhYZHAU3QGv20hVV11B+XnD5Ztm/uzfpWrgBO/2FMcBflO9pkbgiBfddTWELIayo6G6PjyDDrxpoTvuyQH3+fHdE2d8+awkUHagXvZXB186IejgBW9kHOghV3T51P998vjBoSaFmSZDmO/qmfGMTjGTq5EAJVWCIX3U1VYSboGUoRkMsg64jBq1x7D4Tx09lboQVJ7r4n1wlKiR+Cfo3Wkp/ZgPCsbLxH2ML9lQGX3wXFv2jgN2STQ4JNi4TDO3f0lubnX38cvbAgrjOtCRqqT16KJpJ8+ytJBicLSlNKNYDAYUMZGMS/Qaw9WdDwO9ZhL361uCXfKWQJ7WCsBgSmZde1V2Eoa69tg+nJxIOx3dNhzV6sRv+i1jbS8HA//xDejRh7cxOkVy6Tng5F9D7TvBe0mBYlopRfdvO9SukQjld48TsPZ/KHfTytSKbsB4BtGfg0ugq1OGgcFjpcoLy7UrCwh0cbD602EG+ed4eDedqzWVg+yxWK2Wjdqoz77PrCAkVKU/Bq9gIhZ7NkXdgxhk8GfzaRcaocK3iYk2OF+FgY81Fw0edCBnfcw4hEfNrsD4GoQiOO7ryqvKuYw+p4wYRnEjFoPPY5nFHUGTlTFrlc86YRcM7F0ecf4f3ZicNLz2CFL8fb412JmU0w4T0EYv/2sIrqUes7kQqNfS3Sx0e6Q6XIeDQ6NWUC0vEUk2s7b0IfOR2YS/vF7/3fe+g2lDUSfO6odV3RoRyKUueXNSnSDaOF+SC5ZhT0bay1qWilqkFn2qjLSCXSxqYfjLhNcIJ7q0Kd0mQtcaiLVYZGB09ek3IeYCayJRw1dw514tEJKxWcbiwiyBnoDaoonKTdVvUy62x2FRMZPtACJQipW1lujUZlF/KkGIlYO6TmjXn0N3TnivL0bjm+S8oppIsOJI1hXIxWP9IZBT2lvk36IV1sISSGsRjdhPlX6fYf5OlpVj0tJdx3pJaWUqfZaQDtCUlIcUNeH/xeoxJLqOVpKMlRd6KBiAkq2SrcdEmElDQp6q4UIXHb2CVCOkoQ82GtQJZjTp9fNpuY0V/njZDprI+2AV0GL+9uURTZ5vTN/0+c4424TwI+cb0lMZN9Rv+Snf1X+fRm7aZuX+sLvHfkvHoYrDwaPuMcGVfyuLqexooZZbqJHW/uGWj6Ulo49P4YRYq5bk7XWSzzJycGKjElJ5seyyFIqsN25We5+10yHVGF+aRnxFG8WzgbKBYoGaodgXod0nfjtkdqRATNP8kDsSPhiC5cm+t0ZDqHr+Pgi7iJcXdtHV0X+c1fV/OU7kPBtJI6HHBxdwScEjn3xOQNPKVUEJMmKH8Fb2fXq+vfh3/T7KHnU8n4YF2yTxES51yT1E0rmlQ3tzva3kFdPXPMoqZDGuzS8mEZwyEdFl9w+qqw1D/GyKPW6uWF9zjTwHYLt/SYNzILzoUPFKbkm/UOqGW3zgU/t3GG7avREKGxAbXAFLYbLp7/JCgx8Ln5Ghu4BWD+FjLIEgDhkocMwGFc0dUOgUl/AVBLBwhjBFZxqgUAALcFAABQSwMEFAAICAgA9n15PwAAAAAAAAAAAAAAACcAAAA4Y2RiNDdmN2QyODE2YzE5YTc0NGU2OTFkMjE3YTE0MVxiNi5wbmeVVPs70wsYX6LkNqtc5thDK/e1zjhuCc/ahVnN9WD5dlzaShkxI7IUimklVllGz0HmdA6G5JZOKbkNk6VcJmvtcOSaO5WcdfoL+uF9P8/7eZ/P+3l/ed9ML5KbppqBGggE0iS4Y30UGPQtVJUU+aZflAgEUsESsGi/hOGZu5+Jfujd7XO/66A5gf6DacnZxhPowBRd576J/d4hQ5iOaQIN/CDj6pBTnViNz70dGvqAcIWah4OGEWlSaq6ccW51VPI2tqnm3Kk7RvFzo0knx21OiQoao0UGqCZrg423b5bnu++6x7WwNYvMyMf6NsvAUvCGfi2sMnQ+qL3Ls9Dr8cZKuTA6xHICpFm6LmUx/oZauq6YuxsfiZPNNslEyX9gkSMzNs5PF15uDX8rH0gzHsPO91u8VFmC6qQNx6w0ngYaOOWI9A+JiF3rebzx2ZTKvdWFt2Q55qXxUb+WHRpquJPLurZ1ar874ggwiXzKKerghZUAiITm5yvK9wDaRasDRjaQQVWoG8JezQ5mYAvawCnzMGyTj8N7uPcGksJXIVvtL0v3CJ4vdwgqLlNtlNRRX3bJRpVzhK88W01A7LHfUtyQ6TeczUnK6dzHYsBX25IdMauu9BHQaIiioAvYCSMbdv3i6j/r+Ay3C61PSvdeX42mLgX8IqnYoZuFdrKBBk2JBzappPW+mMV404Fiau1ML3yzXwf5ACpMOaOq6tCkT8FGv14hPOTVh3t6GPrVw568L7ECKOR/mgFV1UAXPDmyaW1hdtEzyLB/cE2laZELOwAcd408Hivjxap0YeR6s/xgFHEzAyHXyDkRlu1dHY85/2nb/ZkdbHD3ILOHcYbXOIZPHkJNtvPrkJWd1qJsGtDOCowcflpckpdInESQhlSsSFclpgcqoF/spmHkNigdU7LsDT6Ko0suvq6wN7s1rWd/QssZ3uWAQWY2M9QbX+IlXJTXMOOREJdLzEqC6+drH6TOJAbBcVNBL3pqAmALLATXcBX7s90exqe2LtLoUN/k8nfKw9JzR9ErSx4tCWRbyp+CkJGOs5nTTnFE94KHCw8jF327fnrRE22kMDNpd4bQjmdeEFBcabfjwKa5pvFbope+T6k62zd+Y6O7OBFB8+mjgHns/1kvg5a7mUWiyvRl0pAdQ19S1KCZgZzroHd2sty/9MgFqA+JRPDz4PRg8xUmMxeGNawWN2IQFOgYBauctu+mnf+/AfmC5kvk3m3qZLxiLQfHqGJuXWRszhjnpgVk3kPJX600/xiu968s6aXYGcB9nJKokF4uq8oe49xThtgGu0TAeSzT4szwHwBHAjanQf+bnbmOXot5uwnk9fswfXnEiLb3fmRb7xrvzvkYlEv7wH1dPflF5vUzMaivP1REMjXHNKtENP4xQCOJ2RM4eklxq1qxREWvRT/Y5tBOPg2PPxpbvyZ+s9zHYymE1+Zt51w2S0bC2/KcIB43uOvqKZtGei3wDPqzLanohHH/2oPdn/l+gAbb0BomE31NEFhZC7R2rSqXY12YZjVqaTvN6PCRCCEn1/cKnX4VSI2BY1zxFjCTbg+SLPuV2WFy2C2cF6lpcH7Bd7Zcz0dFaJpnnNp6mJDErpeKVMyb0cmWLl7xhzArPhNZzUFkhK5Yi6k91XoE62BpvbvBisQpoQY8C8WRzmoYFu6Vhuz7XFNaMPBOabupZHE9DAgwemLPP9+21DWcw2NVWQzGiE1w2wunhbs9O/FHax/JcMJu3unFVnmUI5Te7NNmVpbuDBHrFYBkM74cKaIi0DjQmvTV/x04n8Hdku59kql4qyACjoQVHA5J/Q9QSwcIMAYiNFIFAAB9BQAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAANTMwNzM0ZTRmNzAzOTQyMWI5Nzg2M2Q0ZGJlYjk5MjBccjEucG5nAasEVPuJUE5HDQoaCgAAAA1JSERSAAAAWwAAAFsIAgAAAJNUbs4AAARySURBVHja7Z39S1NRGMfvXyWmqalTWyoWgglC0AuBEVhQCGYERlSYtgy0GokiaSGKpoiglm+pRYqYiFk5S0WGbz80iSWxvuPI4+lubitiL+c8h/PDdjwX9nzu83Yul6+GJ9j49dPtHBlytDTPVVVOl5fF6MTvX+3tcW9vBbXXCPC39YlxUBguyB88nqvMBB2gwW3+OyLbH2amSq+oBMI0x06fWhvoD5XI17ZW0/XvL5fA6zanJkEqFMeLngFfwG/GhFGzt2+Z7MKKr7MYpusRJvI18zW2H06nR5Wx63Lh1o4WFco3G4sHEpFxIN5UYmHisvCoVoYie4rhN1hwQYDco8ZYftkph4+ZCHKEjMOjx0DRIasB6A8i8BwKFuW9Qx6fn9qp+gjDDdF3iFW0HrFVSv5LMQILYf5iU+MekZmKG2IJwDz6DXTkwnzUIC8RJF7qSnVzEBoT588KAuhcDLRulEE8ug7KJggcgyozJVsNB1xDQMDZxaAkglVtiSBdCAgIH+PdxWLxZWdl2aPxoMbEoKSiVRsSILnuE/HoPZgIE2EiTISJMBEmwkSYCBNhIkyEiTARJsJEmAgTYSLRTuTb5OTbxobu69deXCjuKL36xv4EK7tut45ENpcc9ScL7sXH+c66bOvi+JheROAXtuTDfnHQ7L1ZEX5niQwR4CCz7yfEN6altGZauo4dbcuyNKUfeZAYT39FHKlPxLnwkbyjLjmxLzfb9J7cQF52Q2oKQZnt7lKZCKKAcsfj5MMB3qtstqSKbQ8z0l0bG8oS+TQ0SMHi6x3yfJWXW5uUIDYjypQlguIqjES+CPr6LdJK+LNJuInANmFke1ZGUCI9OVax2X4iT1kisG2vsuZYQ3lLm/KrskSenTsjLOy0ZgbFgURDyVVZIq9t1cLI55a0oEQ6rJliMxp8ZYmguRBGoo6gmgQmUp+aLDaDo7JE0FlQe4aOIwAOpF5KIuE840SgZ51ubxN2Vh+KQ331iwNZBg2L2IZjsfrnmrZLJXT/7SlJONGgcxddGT7LLTwOweFsWCNGBEZS0aEJlzGtoMSE/5lAJJ+PBH4gAD8Ks3dExTO0zSUH6giKK4GA7/TdvYPjj75PFaNtMBEmwkSYCBNhIkyEiTARJsJEmAgTYSJMhIkwESbCRJjIvxIh3QBVla1CHPu6AdPlZawtsetykZqRMV9jE1+cI0PaEtlZWSZtNMPR0kzyeNoSIS04QDAIz2hRobaCG5Q61gb6vVpXlFz1FO75vviF0ioSipfIYlOjSSVNq0GanEJL0EvEvb1FcpRIK1rhkOUT4SweUhGUZRfXJ8b1iRdyBVKT3COCYCHR3uGCfB2gAAf1qfhA6niG3KXQDuWzLIKFvAMfRLyYiYhGRYaCdkW9RhaHFVneGDhAR95g+PazJs1rcEEDE+unHti12ttjknrG7Ze9wz8RkVNQcQ4SRQeg2FKKJ7FR05yrqvSrrHmgXjx2y2LIiknG+7pGcCLkLzgBotsnkd8YnQgQhEwo/1bgN1iCxBmHToEvAAAAAElFTkSuQmCCUEsHCEBBjFiwBAAAqwQAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAAGJlZGFjY2I3NDEyYWM0MmY0ZGZmYjI3MDA1ZDNhMTdiXHIyLnBuZwEBBf76iVBORw0KGgoAAAANSUhEUgAAAFsAAABbCAIAAACTVG7OAAAEyElEQVR42u2d7UtUQRTG718l5suaumqbioVgghD0QmAEFhSCGYERFaZtBlotiSJpISuaIoJavqUWKWIiZrVWKrL49qGV2CS2R0aO0911713bC87sDPNh9zpXPL975pwzF86jFjAaf377vcODCy3Ns1WVU+Vlgk78/cs93f7NDUN7tTA/Wx0fA4WhgvyBE7nSTNABGjzmyIhsfpyeLL0qEwjdHD1zeqW/zyyR7+5W3f0frpTA69YnJ0DKjOMdngFfwN+MCaNm7tzW2YUrwc6i6e7HNuHvmatx/vJ6A7KMbZ8Pj3akqJB/2Li4LxEeB/abTCx0XOYf1/JQeE/RQm4W3BAm9sgxFl918NtHTwQxgscRiI2BpENWA9A/ROA5tFmk9w5+fHnmouzDDNdY3cGuovQQK5VEJRmBBTPf09S4S2S64ia7BGCB2BuoyJn5yEE7RBB4qSqNNQehMX7hHCOAykVD6UYRxPyv+DEx8a6xoevG9ZcXi9tLr711PcWVbb9f9GiCjaNRZqZgG36sf1uoP1VwPz4ueNZlOzxjoyISgWswCDi7aBREcNXwTviF05YUEgfNnlsVwjkLwgWDgO2jvb9UzL5sLS0a4iCzHyTEN6altGbaO48fc2fZm9KPPkyMp59iHwnnJlSYaBRUwpch3vlP5B11tsTe3Gzdqak/L7shNYWgzHR1Chpc94iEOwj4/RQ7ntiSwpyym+2pbNmjjHTf2pq0RD4PDtBmCfYOfr7Oy61NTmCLscukJYLkyoxEvDB8GYOwImI0iYwIbGNGtmVlGBLpznGwxa6TedISgW27mTXHYeadHcVXaYk8P3+WWdjhyDTEgUBDwVVaIm+c1czIF/Y0QyLtjky2GAW+tERQXDAjkUeQTcITqU+1scXgKC0RVBZUnqHiCIMDoZeCiFhnnMiIYEy1uZmd1UfikF9D4kCUQcHCluFYLHPNyob7cgk9f1dKMk40qNxZVYbPfAmPQ7BYBesBicBISjo04TK6K0gxIr4TOAgRMy8E4EfCecf/EmEvjZBHkFwJBHyn995dHH8keLF4ECJyv2pVRBQRRUQRUUQUEUVEEVFEFBFFRBFRRBQRRUQRUUQUEUVEEVFEFBFFRBFRRBQRRUQRUUQUEUXkUI1o9T7JQCS6vU/CE4l675PYRKzofRKYiEW9T6ISsa73SVQi1vU+iUrEut4nUYlY1/skKhHrep9EJWJd75OoRKzrfRKViHW9T6ISsa73aY8I6QaIomxlUe/Tnm7AVHmZeW2JQzKi3vu07fORmpE2V+NkX7zDg6IQiXrv09bSImmjaQstzSSPJ9MLgYh6n0gLDhA0wjNSVCic7le0ep8odKz09+1oXVFwNSncI9n46flKYRUBZYeIp6lRp5IWU4M0OZmW4A4R/+YGyVEirMQUDl4+Ec4SIBVBXnZxdXwsdvYLuQKpSe4SwWYh0d6hgvxYgAIcVKfiA6njaXyVQiukj7LYLOQd+MD2i54IK1R4KChXBCpkTQ4cVnh5Y+AAHX6BFlzP6jSvwQUFjOh6vrBruadbJ/WMx897R2giLKYg4+wnig5AYinFk9iobs5WVYZU1txXLx6reTFkySTjg13DmAj5C06AqPZJ5FfQiQ2CLWPm3wr8BftAx5nV77daAAAAAElFTkSuQmCCUEsHCL9yNpoGBQAAAQUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADU4M2UzODgyM2FlMTBhNDM4YjQ1NzZkN2U3MGM2MzA3XHIzLnBuZwFJBbb6iVBORw0KGgoAAAANSUhEUgAAAFsAAABbCAIAAACTVG7OAAAFEElEQVR42u2d7UsUURTG568Ss9TMtzYVC8ECIeiFwAgsKAQrgiIqzDIDrSRRJC1E0RQR1NLetEgREzErrVRk0fJDK7FJbI9cOd5m15lRd7gvO5f7YXb2juz5zbnnnnsfOBohu/b3T9D/sn+6sWG8rHTkQomiHb9/rqszuPTT1l7D4ruFwQFQeJGf17c/R5sOOkCD17w5IksfRoeLz+oEwtTfHDk839vjlMi35ibT8+/PFMHrfgwPgZQTx5OnwRfwm9Fh1Ni1qya7cCfcWQzT85gm/DMTFeW//f6QLm0lEMCrfVVwiH/ZuLkhER4H5ptOLExcJu9V8lB4TzEiThY8YBF79GgzT9v46WMmghjB4wjFRsOiQ1YD0H9E4Dk0WbT3Dr59flhNqw8z3GB5B7uL1EOtpSQqixFYMPOn6uvWiIxevsRuAVgo9hoycmY+1qBVIgi8lJXGmoNQGzxxjBFA5mIgdaMI4vxPfB8aeltX23Hx/JOTha3F515XP8CdlWBQ9WiCiWPQykzB1rr9+DpdczD/ZnxceK/K8k0NvFGRCFyDQcDexaAggru2T8IvypN2RcRBvevKZeWcBeGCQcD0Md6dKmQflmdnbHGQ2bcT4uv2JDdlpLXv29ucmVafuvvOznj6FvNIOTehxMSgoGKdhvgnP5J3VCXt7M7JMu2aenOzalOSCcpYR7uiwXWdiNVGIBik2HE/aZfFLrshLYUNu5ueGlhc1JbIp/4+mizh3sH3Z7k5lYkJbDBmmbZEsLgyIxEvbA9jEFZUjCabIwLbmJEtmem2RDqzfWxw9YFcbYnAtrWVNdvn5MyO4qu2RB4dP8osbPNl2OJAoKHgqi2R5+W3mJGP0/bYEmn1ZbDBSPC1JYLkghmJdQSriTWRmpQkNhgctSWCzILSM2QcFjgQeimIqLXH2RwRtJGWZmbnrR1xWF8j4kCUQcLChmFbrHPOylrz6SJ6/9XJidjRIHNnWRmu+RQem2C1EtYtEoGRtOhQh8uY7mCJUfFMYCtEnBwIwI+U847tEmGHRlhHsLgSCPhO943r2P5ocLC4FSJ6H7V6RDwiHhGPiEdEMyLyKGHiicimhAkmIqESJpKInEqYMCLSKmFiiMishIkhIrMSJoaIzEqYGCIyK2FiiMishIkhIrMSJoaIzEqYGCIyK2FiiMishAnLWaVVwkTua+RUwkQSkVMJE38+IpsSJsUZmlRKmHfO6hHxiHhEPCIeEeu2fd1HHyLR0n00IRJF3UcHItHVfZQnEnXdR20ibug+ahNxQ/dRm4gbuo/aRNzQfdQm4obuozYRN3QftYm4ofuoTcQN3UdtIm7oPutEqG6AWpWtoq77rNcNGLlQ4ry2hFQtirrPSiBA1YyMiYpy9sH/sl8tIlHUfZZnZ6g2mjHd2EDl8fQ7EHCo+1AtOEAwCM+rgkOK1v3avu5DoWO+t2e11hUFV4eFezRrv6a+UFhFQFklMlVfZ6qSFlONanKyWoKrRIJLP6kcJcJKTOHgyyfCWUJURZAvu7gwOBA784VcgapJrhHBZKGivS/y82IBCnBQnooLqo5n8FkKjdA+ymKykHfggs0XMxGWqPBQkK4ol8jaNmxW+PLGwAE6/AAjPJ811bwGFyQwqtfzhV1zXZ2mUs94/bx3RCbCYgpWnI2KogOQWpXiqdioqY+XlUasrLlhvXiM5osha1YyPtw17ImQv2AHiGyfivwq2jFBMGWc/FuBf4kNyxnndUuKAAAAAElFTkSuQmCCUEsHCDn4rdZOBQAASQUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAFgAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNLK81LLsnMz1NIT0/yz/PMyyzR0FSorgUAUEsHCNY3vbkZAAAAFwAAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVa647bxhX+7TzFgAXyp15pbhySjtZBnSCAAeeCbFoUrfpjbtQyS5EqL7tSkBfoU/Td+iQ9M0Pqaht2ZRXW7mrJ4Zw5t+/cuPbs6/WyRI+2aYu6uo3IBEfIVro2RbW4jfouv0mjr19+MVvYemFVI1FeN0vZ3UbcURYGjvBE5VypmzjHyQ1naXKTZZm8UTSmOpM2URmLEFq3xYuq/kEubbuS2t7pe7uUb2otOy/4vutWL6bTp6enyShqUjeL6WKhJuvWRAjUrNrbaLh5AewODj0xT04xJtO/fv8msL8pqraTlbYRcib0xcsvns2eisrUT+ipMN09mEFEhO5tsbh3NnFYTB3RChyysrorHm0LR/eW3uZuuYo8mazc/rNwh8qtOREyxWNhbHMb4QnPYpJRhhPhfycRqpvCVt1ASwaZ05Hb7LGwT4Gtu/MSeYS6ui6VdBzR778jiilGz92FhAuFixBhC4dnmIULDRceLnGg4eE4D6Q80PBAwwGxx6ItVGlvo1yWLXiwqPIG0Nuu225TWq/P8GBnPXkONrXFb0DMMIRJcDk8x/i5+wj4cLcxPTSS7Entmv4jhY4iOU4/XCQ9y1A2yiSZOJVJ43eYKd4jNNj9IXaSeM+1IMr/+M+JRPY+My8iUfD/i8TZdMyV2ZAeqL13tEP4dHbZuoRhGYozF/cExZAcMSIZEgmCPEAkRhzWKQR+gph7xhFDKcrgAWHIZ0TsdnniGQgUEyQ4SjASkEqIAHeOYoaIzySOIH+Qz0bITMqAIo5RDKcSx5A6HkwgLmDFUsRBMchnxOAM3IJoihhBzJ2jsTuRICqQcPwIdwkuUseSIgHyieMGiQxJHBIYiFPE3LmxkhXVqu8OnKKXZrzt6tXW+0ANJWhX6EJJOqiDz2alVLaE1nDnsEPoUZYuCbygvK46NMJGw7NFI1f3hW7vbNfBqRb9Kh/lG9nZ9XdA3Y6yPa2uq/anpu6+qct+WbUI6brEW53rkuzd063WsGB7G3x/I97bEHv3yVvl1rCD+taC/LppR3JpzGtHsasG4Mkfq3LzqrHyYVUXh2bMpr7LzGyvy8IUsvoLhKeT4vyCtk3HVaix6TCCR0XqxtxtWohZtP6bberb6CaOJ4zjbPwmcG4TtghnE5GS3TcA3mrp0o2nk1Sw7TeHVNy8fYtmQbR93CIk13Zn7KJxuby3eN2+qsvdI2//N3LV9Y2fF6AeNs6qP1WL0voY8bkMzVg/qHp9F4KDBV6/bFawGoxXC+93BNWAxjEQDFcVrp7Gqbalwp4Gewo8RlthtvvQcT2Fv6pw9VQQvkG1wVQymjniINdF62sYjoa8GeuTC37X2/uq6N6Mi67QDztT3YEf+qWyuxByBN8WYRAJE9ahGHJBMbPpUSTOHmxT2XIIfIC8r/s25PFeThiriyUsw8bgOOlA/TPoFJ4au2jsQC9LP7EFt/rdg5g+eexZfdfUy9fV4y8QMUcKzKajlrNWN8XKRSa4pVr0cgG22QoQhWbxYHeRaIpWQq8x+1xc3oJvtOsp4J7O+Q4yuu/uawgQiFwL9WgBZ6EgwY5L29IuYTBDnQ9N1XddXW0BCUviBz/nf1SrX6E0jv4fqPzCGwnb74hWJMvVvXSj4eCPUm5sc+Ahz+3HPG9th9ZuZADQNwAFT/f2v6/NsV8BNm8uVJFViJSVtSHIuiHf0ArE+XTdQ1z266IsZLMJ/HZWwAAeMBiqvUS3qJHQkCH4uidrq7+T5+IfX/6B4K/Uu7c0bEn0R6T8aogNqBtOVc/257os0beFHvAfgPAgLpfAE1V+cvjZs492jU1ib5uE7iAGt/fduKECs4HFCb5Vv7RNoXcAe76gTj94lY/4fAiU5FNqLj9Oc3mseXyW5na9amzr3ghHASAKHjr0AcMwK7xfI32sUfaJNYIZomODVl/+s6+7r+765QsUbkFLDZ+wCL/fprTjER0yfH9y7yXM+dl9kr1+gmrBjflu2ggvUXSYll3EeFIo8033k+u+yJUHCFRMWBYznqYsoTjzxeKGTBiDBcOUQRNNiXv1/G2/N+z8e+AXKCKLndGrQoeilxdQxkM0Cyot4znOKZGc8jxNM5NZqZmViTV5MldksqoW0TCCvpL6YdHUPWTDcavZs6TyDc27EGxi7g8Mm+DGPa0/EB6o/aYIldANbAO1RP/5178R+VAEycci+L/W34+Agh5DkWVY40QSZSSxWSYzRrnhNsvTXNskJXNFP18o6DVDwY6hSLOcykQZklKXjdRiyqXQ3CrFuEjlXLHPFwp2zVDw06zIFdY0yaXmjGvDWc5NnGDB45hRquaKfwIoDr/4hZDh14xMfIyMYkTwhKU2MUKlWCdxLBkjDHNjWc7iuYo/3ySJrxkKcVKvtFE8yRNDUyI0yWTCuRUZMZRAQ+HQOsS5UNBJdvglLoSMuGZkkmNkYoYTxi3PE8wyTonKklQww42yKssonjdnz1fiAkmirn++Sk/qlTVSa5VwQqGXUGgjea5ognFsmCSJmjdnz1eXg+Kq56vsJCtSZlmaUiYtwZKzVPE4ESaxCdYCMmbenD1fXQ6Kq56vCD7GAqeKqJQboiQRUJGUgIplbAxvm/ATs3lz9oB1OSyueqIiJ2/jxM21MjeYCmm0FJhzzTi8kMO7h5YxnTdnj1SXw+KqRypy8jqeJDi1JscZ1ZToTPOcck1NlmQUXsxJNm/Onqkuh8XnPURN9/+g7/+tbfifIi//C1BLBwjZPbIP/gcAAMYiAABQSwECFAAUAAgICAD2fXk/T3u8qbIEAACtBAAAJwAAAAAAAAAAAAAAAAAAAAAANjJhZTM0ZjBmMjFhNDI0Zjg4OWQ5ZWFjM2VhN2VkZjdcYjEucG5nUEsBAhQAFAAICAgA9n15P2Q+JSdMBQAAbQUAACcAAAAAAAAAAAAAAAAABwUAADA4YjFiODRkMWJhMTY5MjBiNjA3M2RlNTkzMDkzMDUzXHI0LnBuZ1BLAQIUABQACAgIAPZ9eT+bgqF0pwUAALQFAAAnAAAAAAAAAAAAAAAAAKgKAAAxNzA2NGFmZDAyNmFkY2E2MDQ0YzM0ZDllNmM0Y2E1MlxyNS5wbmdQSwECFAAUAAgICAD2fXk/zZrOUlYFAAB5BQAAJwAAAAAAAAAAAAAAAACkEAAANzcwOGVkZjA5MmMyMWM5YzRmMjRjMmQ5NzkyMzI0MTlccjYucG5nUEsBAhQAFAAICAgA9n15P7LR8sMIBQAAAwUAACcAAAAAAAAAAAAAAAAATxYAADk5MGMwN2ExYmRhMWU5OWE5MzI0ZDRlOWY4ZmNlNzgxXGIyLnBuZ1BLAQIUABQACAgIAPZ9eT+gh1yRUQUAAEwFAAAnAAAAAAAAAAAAAAAAAKwbAAA4OWYyYTdiZDE4MjEzOTUyZTAyNGE2YzRlYmIzNDY4YVxiMy5wbmdQSwECFAAUAAgICAD2fXk/syYwX0oFAABwBQAAJwAAAAAAAAAAAAAAAABSIQAAOTlmYjBjMjdmYWM0MzRjZDQzZjRkNTcwNjQ1NTMyMmJcYjQucG5nUEsBAhQAFAAICAgA9n15P2MEVnGqBQAAtwUAACcAAAAAAAAAAAAAAAAA8SYAAGIzMTY0NzM4ZTdkNmI4MGM3NTVhMzMxMzA0ZGUzZjM1XGI1LnBuZ1BLAQIUABQACAgIAPZ9eT8wBiI0UgUAAH0FAAAnAAAAAAAAAAAAAAAAAPAsAAA4Y2RiNDdmN2QyODE2YzE5YTc0NGU2OTFkMjE3YTE0MVxiNi5wbmdQSwECFAAUAAgICAD2fXk/QEGMWLAEAACrBAAAJwAAAAAAAAAAAAAAAACXMgAANTMwNzM0ZTRmNzAzOTQyMWI5Nzg2M2Q0ZGJlYjk5MjBccjEucG5nUEsBAhQAFAAICAgA9n15P79yNpoGBQAAAQUAACcAAAAAAAAAAAAAAAAAnDcAAGJlZGFjY2I3NDEyYWM0MmY0ZGZmYjI3MDA1ZDNhMTdiXHIyLnBuZ1BLAQIUABQACAgIAPZ9eT85+K3WTgUAAEkFAAAnAAAAAAAAAAAAAAAAAPc8AAA1ODNlMzg4MjNhZTEwYTQzOGI0NTc2ZDdlNzBjNjMwN1xyMy5wbmdQSwECFAAUAAgICAD2fXk/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAACaQgAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAPZ9eT/ZPbIP/gcAAMYiAAAMAAAAAAAAAAAAAAAAAPdCAABnZW9nZWJyYS54bWxQSwUGAAAAAA4ADgB6BAAAL0sAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Mikael Bondestam om träddiagram för händelser i flera steg:

Beroende händelser i flera steg, 256-258

ti

MB

Komplementhändelse, 259-260

ti

De Meres problem

<ggb_applet width="835" height="381" version="4.0" ggbBase64="UEsDBBQACAgIAJpaeT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAJpaeT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVfrb9s2EP/c/hUHfWqBxCZFvVzYLdoCxQKk3YB0w7APAyiJttnIoibSr6J//I6kJMvJ2qXtMNSIw9fxnr+7o+cvDpsKdqLVUtWLgE5IAKIuVCnr1SLYmuVlFrx4/ni+Emol8pbDUrUbbhZBZClliVcoFwVl5HJGl/FllC9xNpvRS5rneTYrymRZlAHAQctntXrHN0I3vBA3xVps+LUquHGC18Y0z6bT/X4/6UVNVLuarlb55KCRAapZ60XQTZ4hu7NLe+bIQ0Lo9Pe31579pay14XUhArAmbOXzx4/me1mXag97WZr1IsgiFsBayNUabYppEsDUEjXokEYURu6ExqujpbPZbJrAkfHanj/yM6gGcwIo5U6Wol0EZBJGEUtiltCMMJJFYQCqlaI2HS3tZE57bvOdFHvP1s6cxCgAo1SVc8sRPn2CkIQELuxA/RDikCT+iPg9wvwQ+iHyQ+xpIn898qSRp4k8jXXKTmqZV2IRLHml0YOyXrYYvWGtzbESTp9u42Q9vUCbtPyIxIwgTLzLcZ+QC/tN8BvZg+m5kXQk1bTbrxTai0zC6OEiw+8RyXqRIUnuiwzjz1iZfMG5XoeHmEnjkWdRlPtz33sSWfgVEv36+wQm0f9i4nzaZ8q8Sw7Qa0vbRdKIjbbpwmYQzyzqKcSYGkmKII+BznBIQ8BkABpDFOOSZpDYMQWW4kEEDDKwdJSBy404w39R6pglECMzu5tiSgJFQRHEDKhLqQgwkcClJaZoyJAijiHGS1Y8DS0LlkCU4IplEKGONiNTioQML+IaxYfAKDB7maYQJpBYfjSymZ5kVnVkGUJCIKGWISY1JrRPZqTPgFlr+qom62ZrzlxUbMp+alQzxAKpsRydip4vT2c18dG84rmosE3c2EgC7HhlM8IJWqraQB/E0O+tWt6sZaFvhDF4S8MHvuPX3IjDG6TWvWxHW6ha/9Iq81pV202tAQpVkUFnVdHRPBy0xgUbHUTjg3h0kIzm6T/KVXgCWy1Qvmp1T87L8spSnEoDevLnujq+agW/bZQ8N2M+dR1nLrZFJUvJ698QrFaK9Qv0DchVq74BsYT1iqi2vDlqRDAc/hCtwhoTTWZnH4zq0R8xmk3I6IMcdcFt7sWTJKRJNCNROqMpFnu80x2FWTJJSUojEiZZSBmNvWixGyLED2IwftXKcjy/0q9UVQ6ucNa/5o3Ztu7lgKWxtTa9rFeVcAhxeY1tubjN1eHGQ4N5Xu+PDa6Il5+vnNcBK0MYx0jQjbkfHY1VbKAijoY4CtJjTZbDOZ2FjsKNuR8dFYLXq9YZSnsrKenFSO3qGQnOssYh3zb5bS3Ndb8wsrg9WWrp3203uRjwc86S/kcs59M7+JrfirYWVQdnDORWbbXPzhHSS1HIDS79QecQboP1Kyrgd0uxakWvd+XeZN5d7pSMkXpv27F606rNVb17j0i4o8B82ms510UrG4s3yLEF3IoTpkqpOXaQcnzP5h+aXthOge4x1jWYmVuzVhhqxKDAurLCu1hY8MSm36FphbbPW+9kQHb4xj3Yavfk8BQW2BUu4QkWyinW46d/4p6TJCqxwUcaGAfO5bZ2ModILd0D0IYEVP4By+KdSI58jeefASvwqllz+0bs3Fbxo2jPHOnYvVXlXfdi9JwPsEQ0loHFRyOER5bpEgoaZOjycaTOCfYG6/Etvjm1ewcNl+zkJ1mWwvVijzHvjHtusbwGk/kP5ZKHO8RBWMPBC4Vj9zPo4yK4JJP4W52GlfSv2l/RPoURc5UspLnr0kJtNrwuoXbPoyvEcKvRe8GpZXPiQMupdTJwbHlPsB0kJCazNKVpFhFGkwtAbU9NgEYsjZ927t6ans1LL72TeS+gro4PEXv5LxE91bVxQO3rb+WH3A/fGtNTZO6b6wJ132IXN9oLcubYZnP2PPG7d2rWA0Ge/1Ag/5q8/wLMB399Geb4RPgenE/Hxdu9j7pf+s//BlBLBwjEy+o+ywUAAIYQAABQSwECFAAUAAgICACaWnk/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAJpaeT/Ey+o+ywUAAIYQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAYgYAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Repetition inför provet

onsdag

Några lösningar till uppgifter vi gjorde på sista lektionen.

Khan Academy

Veckodiagnos 10

Detta är en lösning till uppgift 4 på veckodiagnos 10.

<ggb_applet width="1366" height="611" version="4.0" ggbBase64="UEsDBBQACAgIAMitfT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAMitfT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjbjts2EH1Ov4LQUwvENklJlBR4U6wXTRNgkxZ1WhR9KWiJa7Mri6oo+ZKm/94hKcmyvd1sLm2DAnEokcO5HJ4Zjnb69W6do42otFTFhUfG2EOiSFUmi+WF19Q3o9j7+ukX06VQS7GoOLpR1ZrXF15gJGV24VEWcf8mYaOYB2wURFyMYsHCUcgFCxZYUIGZh9BOyyeFesXXQpc8FfN0Jdb8WqW8toZXdV0+mUy22+24MzVW1XKyXC7GO515CNws9IXXPjwBdUebtr4VpxiTyc8vr536kSx0zYtUeMiE0MinXzyabmWRqS3ayqxeQcB+FHhoJeRyBUFFAbg6MVIlIFKKtJYboWHv4NUGXa9Lz4rxwqw/ck8o7+PxUCY3MhPVhYfHhIWJH8csYDSOKU7AiKqkKOpWmDijZ0rIkRbGfEwjFrIgigI/JncrmU46n6YbKbbOOfNk/QahjdRykQuIoWoAGFncVHAoF94NzzW863qfiwWv+omBO499WJdvQDghoMkhCfMYPzY/Br8A4y6Y3igAXCuVW6UYvX2LKKYYPTYDcQOFgTG3hN0c9t1A3RC4IXQygdseONHAyQROJvA/LkbSxUhJ9PAY6ccY7WGlND43ScO7TRI2sNnq7I06H+4LtLNJQnywCabsP/s7s+jT97Do3j/OIAv+lRCnky5Vpi1RkV4Z2fYka7HWhrp+gsLEMJCgEGjKIiBciEgCQ0QREBOREAUhvJIYMTNGyI9gIUA+ipGRIz6yPA1j+C+IrDKGQlBmZiNID0TAUIBCHxFL7wABqZFNEUgX6oNEGKIQNhnzhBoVPkMBgzc/RgH4aLIjIiDow0Z4B/MU+QT5ZjOJEGWIGX0kMFnHYuM6qKSIYcSIUQgJBsnlEgvkY+SbaLriKIuyqY8gStdZ91irsj8LkIZ6dKidrj4dldZH05wvRA7XzdycJEIbnpuMsIZuVFGj7hCpm1tWvFzJVM9FXcMujX7jG37Na7F7BtK6s21lU1Xo7ytVX6m8WRcaoVTluPdZ5WTwTHuv4cUfLATDhXCwwAbP0Z12FaygRguwryrdifMse2EkDqUBkPyuyPezSvDbUsnjMKYTe3NNRZPmMpO8+AnIaqwYXFB3kdmK3N1jcN10jqgqm+81MBjtfhGVMjj645BillDmx9jHAZScvVsKfTYmMYZbCpZoRENwLeUm9/DYD1lCEpwkLIoYoZCY++FaHCVJjKF4ByzCrXGx6c+I70Qf/rIyqd2Gbl5e6JnKD1MWgCte1k1lmxCojpUJ67JY5sKSxKY23PDp7ULt5o4dvtP1el8al5wDi6UFHkFxoCEEA8rgfvDQwr1bGeNZL4WtDLYSuKObzPp1klArYceFG60U8Ne51kZKujAJ7sxIbUsa9o4Sx5LftAtNIevr7qWW6e0hUiP/qlkvxIFCpdLSJNAlqG3njs2Qf9DMdHJCxakugbmZXglR30lOe5WekRM23VyJPJ8PRSN8kKQtulrkpl6oAqHVPK1UnlscN4Pn1Ga4faxM2C3sOd+rxpQQiO0ZdK5NzmeDu8JMf2vPqb1M4P250zo73GFm9qc7Z2dgS4vqe+i48iOlruA8B1DE0YYfQL+dRH0xyHO1nUM9lDz/JpO1Onhnl17DhfRalv2RiN8bWP0BBlmJ7KhMnJ3C9FZU4FlbkSATG9VoV2AHxSoD22t4dQst5Nwk249AFjebiWUlOo7ltj13dLereFhszqatqmeVWr8oNq8hk08cmE46L6c6rWRpCgZawC1+ewgP2mDNoQk4iteUUMDEEaOWtaExgNbUK4Mh1BABV8MS9sLdACumguZiDQ0zqm2RKJq1qGTaJ8clsS09eNe0AdAEj9sgzOEhtfgNeHjoNNy+AZQg8De1BA6zXHH7MdAzE1gwxMmqe6my1jjp0IPDsSFCES9dopZCuBSv22qHSlBni+XAGd7sZC55tXf6BtnrYHgnILMzQAgm4f8ckR0kkTYfwz0tIOd2YObLS/IYzchXnQ17TbkW5xjGdqHffgbWUUk+1O4hVKbxXbph4YYeLfxAtIZJqdGuYzPa98eI3rgPfleMjde2Eg8bMDd7ktL343Ut4ZubtKD9cfnnXRDlIOOdbLgfpnspRfApqUbkfXE63OA1dJe38Amt7VddTyjz8FxmmSh6Jj4MsxE5BS1V6zUvMlTY75gXUKkqDSF7h96aQ5e6M7cuRARN6t4+uuibuhOYOb2ttnfwcPbZ8LBj4Qh/Ig4ew3kNB3mC5MyheHmGIL8fQcOJHiD+MQw9L3ofDN+oy959n9Jvhgo/gMfi98Jt0a4ZlOsyl6ms778ujtBZ/KfofPiVcE5L0iI6IjQJPyWqUBDvRPVh1YA7Di/OOHz1PlXg6rOpAn4UhmGPuU+CgPZ30qDL+CQlYZ6r8rQm8PNi8Cu5H8rT/shsOGmQ4NP6ju7oARCT0LcYh+SD26OzT9GHUnUI3GTYVdu/PbR/jX/6F1BLBwiiMtzSPwcAACoYAABQSwECFAAUAAgICADIrX0/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAMitfT+iMtzSPwcAACoYAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA1gcAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Prov kapitel fyra samt mindre delar av 3 och 5

fredag

5.4 Hur ofta inträffar en händelse?

Relativ frekvens

Sid 262-264

Intro från: GGBtube. DubFet textbelklicka för att se hela simuleringen.

<ggb_applet width="379" height="232" version="4.0" ggbBase64="UEsDBBQACAgIAKOAeT8AAAAAAAAAAAAAAAApAAAAY2IzNjFmNWMzZjgxMmExMTUzZTc1ZTY4MDNkYjUxZWRcbWFpbi5naWbtlvk/E44fx6d8ShijiOWbctTImSNHxJD7Jkch5MgIDR8a5ZhcQx8t51DJnCPH5mrCNEZG9nH3mdJyX2FjOfb1/RO+v3+ej9f7+frp9fs7zc7GFMgL5gUAAEBzM2OH43Y+PlOek8c21NjfAwBOAuysnEw4HI7cpcuqKqpQLW0LQ1ULQ6iDNdTB3sLdHup+bA8LX7fjOMC8HWB+7vCH7r5+vvCQ48AQ4b6IcBgyDo5MRKAS4ahjpyMwiXDMcwQ6C4nOOQ4KU4gpT0eW56LwuUh8IRqHxeCrMeWNOGJ1OZGAwzfiiZ1EcgmKikVT6zD0OgyVgCN3EqmdeDoBN95HpJPwGyQ8pw9PHabSaWQ6jTo+Q6fP0jcGyRszZM4wmTNB5cxQd3/QFxYWNrY3dnd3Af/yL/8Pl4SYTsfFFeFg4wgwmJ/0BwB4ssyNDZ2ip4fy3UIvUIT6arLbUtAQ9gv+vv4rrloG8cElTaFStwjvUgCsvvcXG9OIDcYOmBrEbwsmvzlFWDbrEM0FSWV8zh6LPKhpP8Pf6U9wT5hnIEs2Ol7x+2vy/XHO4G7R2k+BcpvBV5kn37++52H6smyh7WRVgFdwVgv4wMXQeUr9PwHD8ZT3Yy4yJ1+MwPGRmer2YJOuHxmSx6MZBe9vACQn6T6wThTkAOtxWWIL2g/PKxlYFnO8vg2KA+/dRb5ll1NslTtLdWoelaHeJDQbReWN76Vsi3HGb4z9KjJ1JaSw+4atc6Wc8g2+FkAVwnIjbr1YTP79c7mjkrZ1BWPcOnp7y2A2rk7hDarMSJ1rXXQ91IVU1fQS9lfAkcBVjZ/++8ndT3hSxw83wojI065HVgmeGTJJ+qxq4RbzRoFEWNFOp8dZN16x28WiLfYXm/R3spprNI9IhbKWT5S/CgQ6uZBuhmnWb6F2nweFBBNVcFYK4dEikWKgRlnd6pXNDZf9kOIxeE5fs5rTHjf+Ms3uYKFft1tj0bZGvC2vpGethbmKTXWki0ufE5twVwlZwRFyO/wf5YB4Zu2qyiJ9n7K3KwKqmmicUykf9m8HBqA18dmEGxUiIWUrwluAxcLl9wb5ckU6B4Njan+7hReHDelWBkzfdqvCN/HmpSdLnh5IpuROL1nPPJZm7O+WllS6oitGv03HSPReytTMtAXXxvo5g257gy72+AgFcPfQG6gB9cTnDXVztAOf8yIFJ6QivDJwMvoGQ0YPcyD2qD6xXaHs/uT61hjkOkNPkwCdNkHclLeIjJ3OUGJH/WoxR7pdBvoTubMs/PjWFrX4TXdf7azeYcWIfN+uVLVGeNh4gppqy1oo7KTPhZ4ZRh+G27iNR9qrW7lsgoX9Uigt1cYk4UwN5EBlk8JoW3CwfPbkllcFLUMj8hTVPKx0jW9epK0pqUfrrpPUzacF9/T5F9luwWkTZB7rT2PXTzW84O9PKCbNWAv0NrqpW3Mp//KoiAG7C2bll5VRfv5gdPympc+VwSAGlS653npnsXfODdY2DYJKPvZP9RvBoMZXD1wLFfX6a4Jcit/VYjGhrwHSSrhsIb61xoQSHarPTtuzgifFyDtbID4I5XOe1592ygKB8fSMloelowQ+PeD0E+u1m2UfYqCRS3PnChitb9EjZsse0DeOOwaxedAl9yvaE8wIo7VOLIR9GIcdEq4bUOfdjGtICqpJ/WvvqWeUx2cDiYQImPynesWzPTuwx/K2Bi5uky7DO6rOVxid5fcttBbpDfEduNO1r+hcK/v8tob1gWDt5Os82brbn1XM1vPsZOfwb+0SmTR7aWjXH5Pmznmd1PsJGpqb110tRfU0RZ7RJ2o71DQ2se26Xo9QzNEfzZzP92PxPUfKISEPInby5c9peq4qnqo/0vPVG/nKPNEelXxXQjcbdzlHqqnahCI19UM+X9Gsb6RVrEvhRjK4nthdSWrw/+GCkTio5i09AtU+ssChTSq1taa+A2ZwDnx5MnZi6PHU+jFwjI92+aHC3M/TPlG1ou773M6VBQRV66LO9q8mnzxTKWtk8+vPoedfBLWQ3edzrW3/kFN9kNhr6q+UGa5aXvfwAe1UhWSphBiqWz0ilj9zABIcAOpj5ISWLbPzJz/hdxGTeODZA/QtIG5uZN/ScqkjegKepjYOrkHIp9nZ+8QKYeTsK9xm/Nb2ZGa1dwaU1pufEZwH1fHEPe3VRf3SPaxceuchrDb2vXQoTIUudMTs2bS3CpooX/7QbD9647GVpql4+QXBF7kyqjZy44aBbx1XFRlzS23UujWmW3THiRKVpwsWEmcnQs2QF39BUZvPU2zF2zS4UtxW2zyz8+A3dJZe05O+DCDCm6sUwUYhvj1QC5YgU9W+dc/B2y/u8B8U/QmkGr6aVNuNncq1cKwsip60SZBAn2D6vXFiI16y7Dj3UCQBSOGjq7or+7rqXXvx1kMxZN5yKAK+fVfoo+/e/VVLWkBK199S53eO2lnAgZmVLRHl5dzpMfnoIQCzqNayOZf3Z2g7E7B0S5PESpf0khwlEJSKGa7oCwiDORVRn/rf4yrowAOI3WNlFmmnMudLNfsUb/unTryHkr/yL9lv0pPfXmN37640xchrp7WzxmCW+CDTSR8SX6ecqCmKBNRgxZMnffIlJbofiTu2rJ/BQtQCmYthM3wHYStoOD4kwhlPM/yb7CBa9tbJ+XxWdW8waFVrak/kTY/8jFmmmgr3AFBHrdWbG4HrXsL6iPfLWtBw5uTzenj1O4E0nyoIKUfi2jvx+QSldeGKU2NOB9fWWa+kYwhZ40BhjwlBmswFv964tmJP/oTR/sQBoUTptMTamRv76RuV9Q86Lva4fl0auCXqk4rrEcRqgdts4H2QWgKwaehAZ0DSSljVjV9FFNcztivf8fg0jwg+WnuKsVJG49Fx499USKuxF1TxYqZO38m4ovM7LHQg+pIkJTCc4PUgK3U2DQTlPROieEBe/fRFbX/SduP8fL3L/nuXjUzgSJ2zuVw67loRqYUTa/N6seayvhkqCrws3xdeQe61pjMzS/Tx7Yww9kpwPMxwLN9BtLkqnbEQWVZhW22qUzixzzvBG+ENAl1zt69KKv1zAygp0a5whQ1na8Dx6QVf3L9jY/w8Px5qMRhnGpbUTifSwPld1GruZuuHsx+OVFZvwqYV+iFXFzqy/fRrgmV46wcq77CGOga7Kx4EbBdaR2Gmvs+tBQllv9bsPUProsQt0vX1cHkgv18tLOo930tnP/5jA2l+dUIiykb54wZms/ahu7JuHIx1wXOWHsanT2S38Kfmmp+zyVL6yLFyDLyV9FIooikaPbKeD6B2osuBAlkxEWzfinbHBBZl3fjbRd9phX+ih61Yz54dClY1wGQ9we6r/3tXzE1sjOug9xP/C1BLBwhg3Rzv4AkAAOALAABQSwMEFAAICAgAo4B5PwAAAAAAAAAAAAAAACkAAAA4NjhjNWUxMWM0ZGNjNzkyYTE4YmU3NmQ1ZThmMTUwYVxsb2dvLmdpZiWUezzT+x/Hvy7TcmtpZVFKym2WNMevhWLut8UMNXeOS2eicreT6xAtSSuXJtfJbS5poZ1x/GKSrFxaUobEji7GUX3r4Hx/8/g9P6/36/N+vN//fj6vPHeCg4qihiIAACpOjrZE6Y2WliFcTur7Z4g+ACAHuLuS7Hg8HgyOUNMy0D6oZ6F5CH7I7YDhKSOMqYmJJQaHx1mc1rEgHrUm4fDOOAcSHk+wdyXKYii7zKNV7dMUThdibChY4gUdQpalS+o+7yKd8JJfAjOxYQx7MsUhONEuuNAqtoSiivztkFmJKvK6zgmiKZno4x+L8yzGepIJiT7+YeTQCO+w+Fx02DWbmNAISuKFi2TsVT/SdWJcTmgM7aJZzpXg7FgqjUpN88kopVxhpNJy0q4W0ugM+haMQgZDzr5JntCrHNSxPWRY1kcECxbBIj+oxM8BEetwCginQPBYEEFdg8dCKkkQggYdPttkQHmwL7ETQ+3SihHoZwv2pC8ezp13JnTbUVusae22eQMUPDMkvCosn03Nr0fRwX0MEF30l0nlmnWpwKZq3rJ2zZm9hqJDKAakzYCOlEAGTMiECZndh/Bs6GxZe8LtthxGRc6dRgaDWcJkFjLZpTUtxIphYt1CcP1g5v1+cvci6QEUOLBOG55hAwAHjuABwJg8XARIhRADgBiAs1F4HspAiNAe2G0qhiNECJQQYfAesU8CABIALoEjJAipUBKUNggAIAAH4XAQgQARKBCFggAAgsMhBAJCodjaJn+ij/INDF6i0e0Ycrut67CZxaStrVhbW2JgAGlrr5uYgDgchMOJ8XgIj2cRA1rP+HCDzrPS0qa8vcVE0nBY2GhsnIRIBInEdTIZCg1dolLXKRQoNhai0Vh0OquQwWKxOMwKFovNZknPFiw2h835PzyO9J1tuUBAp4vodAGHI2lo4EuHPD6Pz+fzBCCdvnHzJshkQkwmyGJBbDbE4UC8raWQz4f4fA5fwBdsIRQIQIEAkjZCISgUQkIhTygSCkUCoVgo2gISiYQisUgkFktdvIVELAbFYkjaSCSgRAJJHQQhqSDIszKlRvolZOKIBE/AanEyHABgOk621qSkqXISJQrphTyVGLAezuVGDydMLde4ufjejNgp3/zjKu3HwdEDuroWyDHbTbme3fJp6Vawfv1MPOlgUf4hBXS1u2ODSuYeX0UMcWrMZzKa68I1N+d2YGN52Lf4axt/h9+iiu/F9K6Xr5VTd74zybwQM4IHfrS2Hh9JpL388QL7whML6NfiNzNVP75ejUx5frLab4lya8NIhaFy+/Kd//p4e8f0mJv5JR/s9VhxgJzgm24Xa2R+TqfRVGO6lRLc/607OYFxy1SVONzQ0nhK5NqMChYLkipXT08KtrkmhwQGCxY0m8X9qwl9+oMTAa2BS3FuXFjd2HjFmqIOR51eUIkdJ6Uv/J4ww5ppvM723a+0WYcT89e8i481eyYkjGDKi4zPbrrlqfskP+8SCOfNyH/oaQ4GZX2zqC/hjoY/G7Gij7Sk4CMKRpB3fKlRg62uLDW/FyiRNUsbZWB8p9+vjHVw+31dI8PI6fg2Fg7b4JqbtCiw7Gzb5dVdEzXFFXmLFJVhzRZNNPuHnWFPnLLmTeRsn1Q9Hn0X4FKvPnoOLLjggRV+V5s6wKip1/06cKQ98La1Suve1R9j27LyTlopl4Va36vNU2DI6+VLPNKHe96T37xBWd/Q21HbPpwy0ds+R03haBbqZTwnqQ2kBkkGrNBfX3o1Be1kRgbDzu9SmI0b6q63zN3BCWv8kJSe2mAd9tPQyvSqud3ykHUcg6j6KeXFIIKC+mfSS6Fasb3ixrdxXo/hvfi1NwVGMx3H7Ew11TH81/Gf89ePrakNjIk9bjULj2Le31rwSla+WLn5Z/guEzNZx+myHGRYG2F4qbv02dWgSlUFLa26MmIrvsB5Zxr+oQ5d5hrq1KvL6NLfzZrw6DzOmODX9IbncLX/TB1VK560vGsn+xH9xt7U/WNm1cNk3yxxmob7q69zS30Zl8JwasAT8WP1uTLnKxXt5tkPMk4O6x/BOx7qwPmhNXTca5M/P/rKTHFXejZa1mesfnv70h4nu2suC4myyG1Rq4l73J9RnKJLyi9d70dqCBPe5758/JlR63H/ezShv+H6hpJWWwd8+EGdtffeI7DZoi5Q7+3iAZOsyr/6v9+vWOkKT/6uFoFGZuvralxWidzfTpn2I6c2fvxYJL+7Qp/yx5B2dkWIwRVfAqCq+yUlmkv2NBrqQ8JgNsZN6YpFBLqJ6qvxo+Y/Qy72LL+NSvMsMpJXdiVF+Zw40Xb+Ybjzxr3xAbrMpPfdxlBz8fPAVpheEWpWP12/7uYDI/+NZlaG3tDhiZGTws7J/siGKEZwoaau86PeYn7j2SHsGUXApZ/qsDyw0SN/03QIKdeBV0s40fUwAJFb8I6+11Fm5W9xXMdTTPSOb0XZNz4vtKRmVenSk4x2QJEp40KLwpCuIazD8mIu5cmlwgJOcWn9THHZ+YVvyWXxRLfYmeUv/o/OEF58KFz/tDNgZbP6lyEsLPj83tJp1fLXbeFKGA6SNPfJH7j3NobxiP5F/YigXMWZcNufyjj3qXO9azI1YLfj/OXOdnt/kRp7cfbps+O/fbO3kHDdGTPc6rtylFkz7/mqQp3qmF/r1tVtVv6dWHa7QcMCx8fig+3bpTnw6kx+34IqT8+4uVcBPeGVUJQWpOz9+ve6nmuOtwwv7Db+RPhqjB30ULgku/ozMQgzq1kQ6o4oZoGHB8/1NTowPQd7X5UVfAaW7MCWaou7qdn2Mt3j08dyihMyFlPm8lCuK1ohZZ7pHv/AOMdOnd6oWDXeJlEC1TRm86XZCTjZEWxb8EGZ/wNQSwcIqAfJRXEIAAB1CAAAUEsDBBQACAgIAKOAeT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAKOAeT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3ZkqPMlb7+/RSELiY8dktNroCnyo5aet+7qqsn2nZ0IAmp6JJADaiWDr+An8Jz67t5hvGb+EkmkySRWIRAK6j/+hcEJJDnO+fkWXI7+tP9eKTcWp5vu85xC3TUlmI5PbdvO8Pj1jQYtPXWn/74m6Oh5Q6trmcqA9cbm8FxC/OSdv+4peMe7WnWoK1Ci7Yxht12t9frtS1d63ex1u0ZA62lKPe+/QfHfWuOLX9i9qyL3rU1Nl+7PTMIP3wdBJM/PH58d3fXkZ/quN7w8XDY7dz7/ZbCqun4x63oxx/Y6xIP3aGwOFRV8Pi/37wWr2/bjh+YTs9qKZyEqf3H3/xydGc7ffdOubP7wfVxC+mscteWPbxmNCGNtJTHvNCEATKxeoF9a/ns0bnTkOZgPGmFxUyH3/9F/FJGMTktpW/f2n3LO26pHQKoZhCdEoqQqmGjpbiebTlBVBZE33ws33Z0a1t34rX8V/hF3FIC1x11Tf5G5W9/U6AKVeURPwBxgOxAqbilimsqEgcoDlgciCiDxeNYFMWiDBZlMGopt7Zvd0fWcWtgjnyGoO0MPMa9+NwPHkZWWJ/owox68IjR5Ns/WGH2vZYiIGcVf6Q+wmr4n6B5jkAw98XAm1b8oPwc0oxyn4NrEYgWkgcXkUcLPijoLUMfIHPfI+qj8N/wv8wXURGJ6S+K8/U+SPFOSDx6LNXjKNIIxb/mZSOpCayxz3UEGQoxuKgDhTB9oBqTbKIAgx00qDANUABRMGGnQFcoP2oK0tgNrCBFV3g5gJRQIYjO/oe18GVUIexl/KrG9FAB7ENYIUgBoR5hhWmPEuoi00uIWAlCFMIe4p8HkL8CUQVTdoZ0BbM6cjXUACuI2IPsnH0eKggoiD8MNAVShfL3AczVm+q86uyVUKGqQgF/IdNkpsVCg1l5XUGcGhrBZTuTaZCAqDfuy5+BO4l5wUqzNmjW0ok2KdEQ/nI0MrvWiNmGC85JRbk1R1wbwg8NXCdQJBOpuDb0zMm13fMvrCBgT/nKN/PWfG0G1v1TVtqX3w7L9lzHf++5wZk7mo4dX1F67kiN6+yOwNxvGNeanaC5G3j+Bpm7Qed+a7nfddkdZepb7Puu58viZr//gpeYNQsMyXfO6OHUs8ybiWsnyTh6HJqZI2vaG9l923SumLDyr3BclNjq8GZKWh2IgKyI6/UvHnwmwcr9F8tz2T2gdiBAiGCDqoSwHy3lQdxi7+gQqCGoGoCZF8Du+D2T6x4kHUo0QyUGAAQRRJkoPCy4h4n4tnUbs8i8t2bUDj2u2nMnL/xTdzS7FAJwZk6CqRd6DKxl9DhZJ85wZIVCEqo2M8e9m657fyGkA4l3XT5M2JkqatAdhsArHq8kI2YYHbviGJbhVYtLqWEZNSyhSnGz+/F9YMCwRHjsimNYismvqFpEKpBkAlV+xvbDJk1tRYojmysu/dy6Tx07eC1PArt3MyOVP/B2Ou5aMxniBc5t4YoIHyv5GbDFzxw9Toni0Y3lOdYoknzG8qk79YUizylF3+rZY3YqbkTAmZypn1idxNW+NfSsqLw5Cn02AWt4V50X6szl8FVPPXf8wrm9ZBKTqQAjw2NSxCrB7YO4HZIZ0iRpOPJ7nj3hcqt0mS25sWaS2bd9k5mi/rxyckVmL+mFrwzsgGPJVL9rdu2RHTwwbZ8G1y6TnXPTsa2R8oZ5aZ7pMfezz9osxgSu2SNrzC4rQSi8znRseXYv5pkZ+oWsttOI3nbMbs4xxe1+Y61pmtOSsF+O2P0FAq6Yo8m1yf3JqLkYmQ+WlwA1fNsbtx99Oirnj7gjqoxtZmXbTKHG5j0zrOx9XZ+1tAFzxRkXnZkrLoQpaqmAqnJHnz1BCeK/Hpg0UP5jYN/Poc1Qs38wcTIT1Mw0LWBW4Ia5t37oegWR4oc/ntv9vuXE1TVjnrOGcCLoVZgN4h+7Ytbd55+LXzBhKIQNz0w2IgYtZVU3zSq1Qw+CUxrSIk5Rdc+cUn6v4M1wq5fmFu7Ag+AWNaReAXXHigVjdhHlMXN/f6dsnG39THsIO+Qg+KaphuQbBvtSM8j4hlbk2/3EY8/w90aon7QUdvG49VvzkdL7T/me0MMT0UGS1dGN+OElPJ2z7fNMhSpewFa1JFvnHQ2fcyY0uZwxvIlQfsx5XGGVuQ8qnjTmr6ZclGKoTiVUvUdKvypUp8ugyhd/KoDih644rA9ViNBDpJVFUKGVoTqTUHUfKW2zKlZnq2G1Bani3kGo7Vy4tiJU53NIVda/8x0L1bvBwLcCDgwQykYq4rhMOUtLXAEoT1ZslOYtTRiErio+RW03yGupE3mJuEGjUYMmfmwZtKeHAdrGMeu547Hp9BUnTGi+d0cPQ9dpzVJspsoFTjEBh1AxIU/aC5Cmgbw/YU8BUcb6CkSpQfgDHbeu2QEft2x2IMetZ+xAj1vPRTWij+ewTlRD8kZ8YKGrwTMvRb5GgutRUrg004EKV2X6Ytn0rSE/i+vBYdtnTZNNWeQAwkjENBi/bBX0re+OeMYXaR57PBnZPTuIxWjE5f2FE1ieb4VJjGzi5sayJjyv9s659EzH59116eRJWagHNYK6DUDHSPwJK6J3dB1oOgaGpqoAEvikzbtaDo4X1/XhBOxQigkikBgsGkIa0RjmRLS1M01IsUs7HFbYtWGFQDvEvaNpFBGqIwOrKiQqETzJ4YTRXE4k/ZRnK/opm4ujzOm9PbJN7yFJQMoLSfwB4SunWKJt3al73gSw2mlcdJHF3IrTm85UydxyKl8FYkIXa3x+aEVACB0/ZDzi4pTVLLYyhHrjsvksEKWzgBpnrHCUr2LtNgRA1xFi7TYHV4hiW+voBtEBVqkOhYCunMgCarVMVlm3frEXfmZ7vZGVcsLPhIMNMt73zVdQ7E33XGdOIm6q+D/s0b4taOMdxFHpfl/599//RwFZ6ZB9nOkMBaiqV6ukFC17aDm3rIau5yvKvRplNR7UyKf9Ia/cMxzbws0FMvUB5irJ2OnZ98qJLH8iS51A/irEXLETFL30BIfv4pfIfL9Y2qjw8Qb2gPGhOudPFnF+UoXvkw1xHWe5riaaBBUfItuB1uF2IsF3cZOzPe62Kcv24lb75mC7hYh07iBCNexvzW2ci3k1SvMKdfBh8IpKXiEV7otX5U1oNvP8Smaebx4po6qZ51f1687ggrWd3ozXcx0/N1WRel0/pDaWhc8g9WYOqW5VpN7UD6nQc9kKUm/n+n0qy9Tb+iC18Z6dbA913EXdX6WLemkf9e6wEh2uGwSrjHe80D0OqrjHwYbcY7Q4KAIEHW5YBCGLuFP+cSgNK/rHGS15MdeeVB6c8GI1HdlY51+2OdnY2IQSKvJikYb0qqUOeut1nYSRYVcEioenAKRDwcK8QDw8bINpgTeLuNqvxtX+xhJCMKftSwxZOdzcgJpmfWgBw7YvHoC7etv3UrZ9beYhtCu7CC/r4yFIB6G9Qw/h5SJFGVZTlOHGFIVmwQ47z4bRMdWZdkCqkucmtGM/Yc00mj02hzNmhGeCYwObvUpISK+LKBiQHhroAJp8upClEYvqKup3CbD6fxmbttMZ2gNREds5NXs3Q8+dMhnLnc3xnkuo4oSTVkJsxVhNzdAg0iilYZcPibp8qG6oFBhq2FVhpML5tTpfi51KUCQtG8q/FGbJnHSWDIYDjVejO3SkN50pU+NOJj4ns1SuDMW5MixHuxvrZcpW72t6Mfjz3Vf4SGE1Auz/f119wPQ5jKzNf3yfusF/BS6ruPjZyhqawLqfG60JNzDITl3VzJQXxnOUnSQDaOpvaQ63Ii0VRXOd4YILOqUrAISXAaT91PCQX+Epgof+Ck8RPNqv8BTBo//s8GTn5SQtsvBNrHI2+bQ+Njk7iSZJl2eNTL4kQznCzmpDWDIEvbC+Ty2+Ok8yCP3ISrjjPzPfjP5VxKO2GCgfDZMP3c50gDqymYQtiVF5mVlntHggn2QAFov+CgHjRgL2p7bnBymoIiJCkJwMJpe2x6O88phEDzQHkzMWbAYvBilU7pV///0fSgTLDIQENqeoGJd0W3uacYRxrAcVGs4SjVp5CmExhbgihRlPNpxGvlcKUTGFpCKFGWcU4X1TiIsppBUpzPiTCOybQlJMoVaRwoxLGI6O2iuFtJhCvSKFGa9uW1Ka42agyM04RcpjxcnLl6ere5aXITAA0jVCDF3VKYB44UDIDdcey9rj0rXPC981TUUIG1CH0KCU5PTVbKX2RNaelK59bnQNqWZgSHTE14YiOQn0rdSeytrT0rXPC36xjiBBRNf5oomY7kpyNFl7rXTt82JToukG1hDVMQQqgWRHtddl7fXStc8NHfciOSfJ0KbrTkeWXy6wOalNYJNDFkiQdcbJmnol6crpPasLXadJup56//qniOJKBtk1Ju3ESJB2WT6dz56sLVWnkqpSDcOpUdD9tOGmoLiFYuFmponK6wY76HzWCUqI5Ed3OiypaCeoviJ5ghNUXdnuyAqCsoThGhNGEoS9NKdOWapIjamiCapOmSErSRStMVFaUgYtr7QAajWmSk9Q9da1vbJU6XWhKhl4PxHXKyU++/1qIXc/s0odrGzyyk7Efrfn8bXhgIukCUqMS2cv1FkggFWCwqE3WBcjcrSOTjBi0Q3UNH4d7WpM2rtFY9KWZLaTI9KsjYxH+8dPOpOXqh1q8GniKqQGpTpIz+/MlZpwTGdWbkS9Nze6d6GADKoIyGBDAvKzjuxtpogMq4jIcEMi8rNOfGmmiHyvIiLfNyQiP+nSAc2UEK+KhHgbkpCFueXDnjvUTAnxq0iIvyEJ+XmnTuxPSHI6Z9bLl59tP19eMONhyfD3JGlyI43gX/8sOQi+NrSll3a1MwmH64xOvy/W6WTU/361qB/AyC2EpFTkv6XJK6nF1ZEGMdAQEsuIISN3STtjK2vulmHMhyqM+XAwjAEdCnWqUt6a8ZUGMc3li74FvlxEK2QmOfNeWMMPGQZ9K2ZQer3Nb6vNpM7bRGplFs1gXrDgbLjoDLugQoyYZoRIi1nrbaCzGxRgqqrhDb3Ba6EmlefjDlYKL2TLkmSm3KBjJ8umX9QcDLhxNMo0Ah9FI3CRaQTG1RqB8fqL7q7sKeQt+Q1VCSKcvS1PoWmD9Ply+30TOzCE8bY86u7l/DIj5+aymfNpSTfz5s7vzi1O+npyE4UYSowLpR3XTNqX+4/jDMc+VfEfP9XAf1zS8AN1uw1/OVSvqqB61QBUYR1Q/VwF1c8NQBXVAdUvVVD90gBUSR1QPVlmCVOr9S23gzVAduu7DJVB9rQasqeNQFavA7Jn1ZA9awSyWw4EyyF7Xg3Z8yYgC0EdkH1SDdknjUC2Ft7W02rIPm0EsnjjSbLsgqRfZU/RlfJ75bfqI4Woyu+UM1R5cdJVEa20QF/J6DiOAFCHUAPx/kIVI5XCba1+/CyG8dN6MD6rFYzqjmF8GcP4OQEjrrxYZK1glJET7Mi5kyCcTUm3tbHvqxjHL+vh+KpWOJJd4/g6xpGFPAkkSeUNBmqFJI2RBAgZGoAG0ClV4Wa6hnN2HIiBPF0XyDe1AlLfMZBvYyDPUkDSytsT1ArIuGuggxOzncG2dPtdjOT5uki+qxOScaSzJSTL7LX8SXS5XInFoV7IXZSffc3Z/ou9IFotZyqK34rCdvgU5isWw2WufXajZTH9PLcjZNP7LFeZZFJ2QFdhN9R0v51QS6KWuBs27oVtVLdUMfS3NenrbhtZj3y+LxDgTnK1joPhgL2Jna83Ot6gHW+s3EmurVO0BFuzQOdNcD1AL5b7tkE6iduoQSwoY1g/C0sZxsncVr6SpvVLrmGNFmm7E4W/ycI3X6EwrT+qG1a0Q8NaaXLeRkzrXU3EvK2nQ9xU+85CYW1uNSzSIDlfMqS0du27bN7bpJNYfQwXbdfeLNBvatO+F8t9GyDY0TQCgEGBBuEBseBHI5z62NdpN8ytL2NcT75Gy1acSvP6RlrM1wsi12iNUDM0qOyBrnxgLKPX0fKOqayRxbuPXstNb96IkTXzWpsaCvtBRrDd2thX5uNkcqaJ8ay0ExkBEcc2yZdfMmK+NjzItOu4k1xpUj8Y0Ee1Ab1Y7pmPwxdbRQSrlBo6oY1K3pSxs2+lnX0n7ey5NJtnC+xstFK1Ix9w5QN9Gcr2VskSk93ZWbXKGhEbMbNObQQ+E0nBZHaSGLhBIl6Mulsb1LWc/p9EO0NYQJsocjBM6DfEw2xsOFUMf6826YT2EiUAWO0Y6tw/DeLBKsMk31cbJvm+EcMkazGF4kM1ZD80Allt+wNQP8bDMJ6khmFoVYdhfKzVMAw5BBV0EhsPULiZZR6ySF7ESD5dF8mLWiGJt4tkmZDliQxZnsoI5EJGIB8XhCzR1jOWTA0Owh/sAV+mBr1VUoN01yFLyUXLNhKyWA3x2w4yMziok9eW1HSUdNp0o5O8eygs8GsTPGYiFNRJbqCjHU7I7tUG9WK5bwMNdWb3+JZGTeJBxmG5jB2W9ymHRa/qsFzWymGZzVPYzaDwTzGQH9YF8lOtgNS2CmQZx++9dPw+SMfvk3T8Lhc4fpp4YCIf+C4fmErHL1jF8dN25/hVXYt0I77fZN+L6/zMvt/32pjAJb3CEBgdMfRH11WkQ61JnWNLhvXXhgdLe4UPZ2RzUBvQl/QKQxV15nY+VbUmRT3LE6pmjjF9Xi2l+nzPrCy74iVekkuFK7ov5UC9qgbqVUNAhXsF9XM1UD83A9RlizRuF9Mv1TD90gxM9yunJ8sHySTX+dpvRrAkpvttUE+rYXraDEyXdfhtF9OzapieNQNTfUOYZhNAfO8Ga9FuFiV37I7eUTscza7vjqaBddHzLMt57fbEMsQcWKxq0XLCtCRGyQ3NWQVxBXBqKGQDl9XXtzx7EOdKfCZP4Yci5x6UgBGIdlQsf18CRpSGUa8AY87ux4cFIyoLI07BCGAFGHP2Wj4QGEWvB9JRSRhJGkZaAcaczZ0PBEYxNRqhsjDSFIxQrQBjznbSBwEjMoSJgTooCaOWhrGKicnZv/qwYERlYdTTMFYxMTkbZh8IjLpweLSMw5N0tK/CfdzKboRwuyzUFtvCzVZBqU3SVGaqgYxXinf8IMV50fC9icxoz/QCy7fNaCNzP2DnYRAjhPPjcmE+/wrzO7nPK/fNni8fHbWXTm40/7et5bqexDiu3cf9pFY4brePOwvk00VAVhfIpzUFcicC+SzGMTXc9rzycNtntcIR7xbH5zGOT9bF8XmtcITbxLHS2JVzOQb5qRyD/GHB2BVdjl2JHuh/ReKBQfgD85ECK8yz1Lc7diV/r103y+dwkYPZNMyEC0IyjFYXM7rKsJYKaaONELKqwLb1jKDOD7xQk7cLx3/We6fE7GzBCimpvbIoM5EWd+jcX9EEzmaxZNAYlhQqTRtyN3nuDxct1NUsFn1vTMNWebZt3RhRxtiHbhS33c9mxj4ad/pkgbE3xAPX8oHhzNhjYeytr6i6sTd+XmN/3TidOHhLMjwUS6KqSUtyMBzirU0zONR4Q7Js9mVTVKU4VAE6SoYqTeJQzg5NMH+fgvPK+xS8qFV+BOw2z/QyxvFsXRxf1glHYOwWx1cxjqfr4viqVjjqu8XxdYzjybo4vq4VjnS3OL6JcfyyHopvaoXijrvX3sYofl4Pxbe1QhHtFsV3MYpX66H4rlYobrUnI4vi+xjFT+uh+L5WKKrbRLFMiuilTBG9kBmfpetuAlU88U0+YcsepL7MEfVWyRGx9/60SaJvvyaJ6hb52o1hSXGSCGjJ7gZ0OFmi/q9ZonowoncoWSKSvE2LVhKoG4vKmPvX0ty/ksb7VJr7k0XmPhowMpJP3Mguoa5cZ9tcydyDn9fcjxpjW34ac3/TmCZsibknyT4hWLQeWLNY1G2c1hyouTcboytLzD1KdgodmrV/K639G2m7vwjL/Tnf0kO5o0ZUeiwD+x9ylbK7VVYpA1veeLnOlt5pXJt18JZ+3BiWLLH0qXGEsEnNVzGLflSZTFYLrTlQS3/XGEYssfSpkeqkSUmwcvM6IuP9ThrvK2G6P+WbeiQndaBWtHlWZOpvZVA/XWVSB9jyVtB1NvWTxnjFP42pdw/F1KcGesKD4dBtYzh04JZ+2hhGFFv61DjP5s6t6bruyDJn5tUN2cMenlqZzyxmWv5YhtXWXHg3GPhWwFlAdbGQDCCFLDMnoYyE1+bWHmM8+Nc/Xc9mp34Gg/yVP4zEyh+XtmcOLcX5v/8V58rvFSdv5Ed2ERBjr2tUzC0VEQoy7AACDBUDzQAG+8NYoAo7SCMY6MgwNH59fjTIYoFJbya24jiXeVrX2kjMdOyxWKbED6wJfwFrBPyJZfX5gzPVm7AXMkVKNTDxEBk5JLi9bKm81YbFnNleb2SlvOkP0pvOdoldL8uAsbbR7s3N/llxWRS5B3ta6Cqutb+g6YNLmj57aDligRefiaoqPqs8qLKdlVfuGUZtYRlBdOkHmKskEwDPvldOZPkTWeoE8tG14bICJyh66wnmRlXcJmJpxNyGmMlQzx4wkCuow8dDUQe8B3X4uFgdvGVRYlIdvFVX5Qx3HJsxYvW9kuusEJAYOQqBt6IQF4eiEFqHmU9EDUygHo5vEuqhdQxqAF0HEEN+me5KWS4WK4tfTVn8lZUlsh2h932o1gMRrUORzhgPCKa6DrWM5uSIBtejrGhsTKsuD0SroLoHM3O5WHOCapoTrLf4cxStHqiVwRRlrYxg+MatzKdD0QfUARhijDRN1/dsYD4VBSdLBuKlg5O11l0O+bLWLrB1VhNiME3QVUoRBkhXDZhRmaRMbNmyXB2KJtE9WJarxSrzvZrKfF9VZTa4f16dtUZDOSGM4PkGjEs6J3oXKcVcVnSmBDtPikbJu9Ip0SiNaU4DlyvW92UZYaZ+wxkR4Zkgf2AzIIX461TvEQuAHu73epoBTaB3LY32iaUPAFHNv4zcodsZ2gNRH9s5NXs3Q8+dOmU3WeCbVyCxEVm459sed2dcvUWaB5lpvuMzssMUPj8fWu7Q6nrmH/8fUEsHCJpHzk52GgAAbjMBAFBLAQIUABQACAgIAKOAeT9g3Rzv4AkAAOALAAApAAAAAAAAAAAAAAAAAAAAAABjYjM2MWY1YzNmODEyYTExNTNlNzVlNjgwM2RiNTFlZFxtYWluLmdpZlBLAQIUABQACAgIAKOAeT+oB8lFcQgAAHUIAAApAAAAAAAAAAAAAAAAADcKAAA4NjhjNWUxMWM0ZGNjNzkyYTE4YmU3NmQ1ZThmMTUwYVxsb2dvLmdpZlBLAQIUABQACAgIAKOAeT/WN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAP8SAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAo4B5P5pHzk52GgAAbjMBAAwAAAAAAAAAAAAAAAAAXBMAAGdlb2dlYnJhLnhtbFBLBQYAAAAABAAEACwBAAAMLgAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Sidorna 261-266

ons

Här är det lämpligt med några laborationer. Kanske olika uppgifter som gruperna får redovisa på nätet.

5.5 Statistik i samhälle och vetenskap

Sidorna 267-275

fre

Här kan man tänka sig att eleverna gör egna undersökningar och redovisar...

Medelvärde och standardavvikelse

<ggb_applet width="1043" height="624" version="3.2" ggbBase64="UEsDBBQACAgIAPVzdT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VvNkto4ED4nT6HyYU8JY8k2P7uQVIDUJlXJZqvI5rA3YQvQYmzWlgkklbdJXmFfYF5sW5INxpphTHYOszEHGyy12vq+brUbtek/365CtGFJyuNoYOGWbSEW+XHAo/nAysTsadd6/uxxf87iOZsmFM3iZEXFwHJaxJLtGX/2+FE/XcQfEQ2VyAfOPg4skWTMQuk6YTRIF4yJcjPNtjzkNNm9m/7FfJEOrBkNU9mhVbyO1pkohP1V8IanxeWVut065GLMNzxgCQpjf2B53bYlv31gieA+DQeWa9uqhQws0naOOqHJkb2LOOGf4khI8YPykE5ZCPAnYhcyhDay19FdMxBGKOWfGFBFZFv/SjHQZ5kf8oDTSMJUUwQhhD7yQCxgOIbZLRifLwCGh7tamx/HSTDZpYKt0PZPlsQg6EgD7PKLnievUpgx3I/gltvFbWK7todtTDoeCOZ9HmmRnuN2MHHcttvpEH0DtpkwIQBKiuiWpQWh84QHe8blxet0GIeHpnXMIzGia5ElygucvEkRMrBgSolE8iKahyxvw2CmBfOX03g70ew4WvX73VoNUfOZzkdxGCcoATQeTH+ef071p5KRE91L2UrGVhK5Dql03497REmoz6n+1DbkkZ5aDhwXqLFd3IanSDZIgsF5C26U8QeWhbKIizfFBXjN8oBUyv+WraawaMp+s1eJ70ll/6riVf3KcjL8zPXIDX5WGgXMZauoAJ6Pwm3vlCDeC3r2KTmylyv872Y556Cvp2EasPpLlkQs1IskAg/O4izVK1H7qFIfMJ+v4FJ35Pek0iv/AKZ1a8DmCSsMpIOL9gvVa5cXYqW5f1VMQs4hBaP4AmIkGE5Io71lAQs311+TgKHYX6BU0CigSUA3G75kOphlAiLMwHp1/W1JI/Tyzfjl5P3rXy0UUAEaZPhkIVsxiClCLZMoW7GE+3uXGcoQ+6gPc8rymbVbhQlkwI1V9Nyv23zUwSOh/5alBIF2vaDwrYWLoLeDUFomRWl7Gwf5nXFBL1CueICwtdYKIMozFuQPD5EveLQGlSp8lCy2j/taZ8nRNQ93M+JUGfGazoh7YaTCiFdlpNt0RtpVRpymM9KpMkKazkj3EkcqjPSqjLhNZwSy5wolvcZTgi9PmyolRtra+FCCjby18U9gbCSuncZTYmSuFy8xUtdLLDFy10teckleDUqM7LXxqRoxstcGhNftOmGpLO4UeF4QuAU0D6yf/s5i8UtpI/Nn3aJ0HHMp2FZYZQ33SppdkzS7DjpyhG5S3ZatjZE8YIzOsQXpVu6Do3V8/TWa1wboPBSAd6xaI3XGdiOXrVtdtpxGtY3t/j+MbfyYbkBqY5haVrtpbuzPQ/wEDQkcDhwuHB4cbTg6cHTh6MGBbXmSkliKYimLpTCW0liKYymP5QAsRxD7i4VMrwnh1tbxPBQ1+3KqWHB/GcF8Vb2vwG5a6Kj0ecpAGFdN9BSf516P+ro6LQuh5WL9oWatm5/iKvV+vFrB4wFFdKUqejRSaLl8+wBRu2BAzzwTRWvpiak15nrudO/yQCNfxd6ZPnw7ksm4Fg7j2XgeGnN4BRNp2Q5uE7fX9pwetm3n3gDq4FcL5BBC31mwhuT2itoZ8aXGyv9O9xsSfC4iI6x+h7t9B6Safjgk5FxAxg7jf/W1e/h9Mb5pUj/6w+skIyODEdxwRsaXfeAqI0a0bUDKd5oRYxe46ZtZY2MTuOnvQY2NPeCmF0/GxhZw0+uw48sOcJUR8/2FJuwlnc7RjIyk6c/fkZGRND1HGxkZSdOfvyMjI2n6L5uRkZE0nhEjI2n8foCRkTSeETMj+fETkuNNwiFNRguaiMpWofQMRHGeoSFKBtZnuPsT5MqTI09tecL7E8lPX3JmDhuML+Rf/PQs6m4x6iFVb73ZNke1jhIVt9kG26S2dd7NZikTaKvG7uBHzUnT1ajT3FFlPH434HdVUUbr628IXIJJt1iuk3jDRM2640N+UeAI6ez6nwQRG8GQDUvqVlUfLLrxTXash2r8cG02Okal1mg9UKOHAuqq/F9CeV38sfrZv1BLBwiqDnAABwYAAIo9AABQSwECFAAUAAgICAD1c3U/qg5wAAcGAACKPQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAEEGAAAAAA==" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />

Fri att använda. Från GeoGebraInstitutet

Gapminder - övning

www.gapminder.org

samtidigt som vi kör muntliga nationella prov får elevernas uppgifter på gapminder att jobba med.

Film - undertexter

En tanke är att eleverna får en film var från Khan Academy och att de gör en översättning till svenska av den engelska undertexten.

5.6 Vilseledande statistik

Sidorna 276-277

må

5.7 Några statistiska lägesmått

Sidorna 278-282

ti

Nationellt prov Ma1C - Onsdagen den 14 december

Behovet av repetition gör att vi kan senarelägga avsnitt 5.6 och 5.7

Muntligt Nationellt prov

Egna undersökningar och gruppövningar

Sannolikheterna bakom "Kasta gris"
GapMinder