Tal och räkning

Från Wikiskola
Hoppa till navigering Hoppa till sök


Överblick och sammanhang

Mattesidorna är till stor del uppbyggda av mallat material. Det beror på att matten repeteras år efter år så att samma material förekommer flera gånger.

Den här sidan är en sammanställning av material från flera olika sidor. För det mesta har jag planerat matten för ett avsnitt en årskurs, exempelvis algebra år 6. Senare har jag lagt ihop alla algebrasidor till en. Eftersom man kan vilja jobba med både en hel sida med alla information i logisk följd och med en delmängd anpassade för en årskurs kommer informationen att finnas på två eller flera ställen. För att undvika dubbelarbete har jag brutit ned materialet i mindre bitar och lagt dem i mallar. Då kan man bygga flera varianter baserat på samma mallar. När man ändrar i en mall syns ändringarna i alla sidor som använder mallen.

Det finns material som inte passar i mallar, som inte behöver användas fler gånger eller som hör enbart till en viss planering. Detta material finns på egna sidor. Sådana sidor finner du nedan:

Lärarhandledningen samlar kursplaner, lektionsplaner för respektive år, prov, diagnoser, mm.

Övningar, uppgifter, laborationer och läsanvisningar ordnade efter delmål och synkade med boken MatteDirekt.

länkar

Här finns det övningar läsanvisningar och aktiviteter.

Repetition av addition, subtraktion, multiplikation och division

Mått och omvandlingar


Kunna räkna med decimaltal

Kunna använda några vanliga algoritmer vid huvudräkning

  • PPT Tre-gånger-tre-rutor att placera siffror i så att summorna stämmer.
  • Efter övningen ovan skulle det passa att undersöka magiska kvadrater.

Multiplikation med uppställning

  • MatteDirekt år 6A, sid 19.

Kunna räkna med kort division

  • MatteDirekt år 6A, sid 20-21.
Öva på Khan: Liggande stolen (på amerikanska)


Djupare övningar

Extra om värdedepårånet i Västberga. Denna övning handlar om det så kallade helikopterrånet. Den tränar antagande och räkning med stora tal.


Veta vad ett primtal är och hur man undersöker om ett tal är ett primtal.

  • Spela Kenken. Där inser du att det kan vara bra att lära sig faktorisering.

Presentationer

Övningar

Repetition av addition, subtraktion, multiplikation och division

Förstå hur tiosystemet fungerar

Kunna använda några vanliga algoritmer vid huvudräkning

Multiplikation med uppställning

  • MatteDirekt år 6B, sid 10-11.
  • PPTpowerpoint om multiplikation med uppställning
  • Multiplikation i bild och uppställning. Denna bild visar på sambandet mellan en grafisk förklaring och algoritmen.
  • Övning. Börja fundera en stund. Hur skulle du förklara hur man gör multiplkiation med uppställning. Använd text, bild, ljud, film, animeringar eller vad du tror passar bäst för att förklara detta.
  • Skissa med några bilder, stödord, en tankekarta eller så hur du skulle lösa uppgiften.

Kunna räkna med kort division

  • MatteDirekt år 6B, sid 118-19.

Multiplikation och division med 10, 100, 1000

  • MatteDirekt år 6B, sid 12-13.
  • MatteDirekt år 6B, sid 16-17.

Överslagsräkning

  • MatteDirekt år 6B, sid 14.

Efter att grön kurs är klar

  • Titta på PPTpowerpoint om multiplikation med uppställning. låt eleverna anstränga sig att förstå denna. sedan får de försöka göra en bättre presentation själva. GCompris, Open Office, TuxPaint, MoviMaker... Valet är fritt.

Lektion 1 aritmetik år 7

Uppgift nr 9

Placering

Ni får skrivhäften, läxhäften och er mattebok.

Det går bra att börja räkna från sidan 8.

Den som mmissat diagnosen får göra den nu.

Vi avrundar med att lösa uppgift 9 på tavlan.

Kortfilm. Begreppen addition, subtraktion, multiplikation .. förklaras

Lektion 3 Decimaler

decimaltal

Vi tittar på arbetsplanen och vi väljer beting.

Decimaler är på sidan 12-13 i boken.

Se en kortfilm. Decimaler på Kunskapshubben

Uppgift Hur många centimeter är 2,375 meter?


Lektion 4 - tallinjen

Mål. Förstå hur tiossystemet funkar - talsystemet

Introduktion: Vi ritar en tallinje på tavlan. Den sträcker sig från 1-100. Man kan sätta ett halvtjockt streck vid 50. elle ett var tionde. Sedan små streck för ental om man kunde förstora den. Låt eleverna komma fram och rita in tal. Tar det stopp? Zooma. Hur många tal finns det?

En annan från 1-10.

En tredje från 0-1.

  • Nu kan ni komma fram en och en och sätta ut tal på tallinjen

Datorövning: En övning i att rita tallinjer i powerpoint.

Räkneuppgifter till tallinjen på sidan 14-15 i matteDirekt år 7.

Datorövning. Matteva - storleksordna tal

Lektion 5 - Multiplicera och dividera med 10, 100, 1000, ...

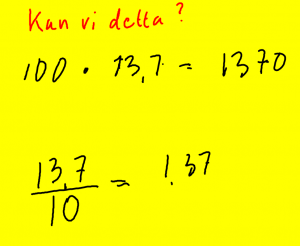
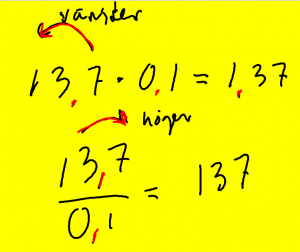
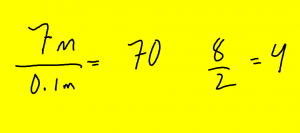
Mål: Multiplikation och division med 10, 100, 1000

Förmodligen kan du multiplicera med 10, 100 och tusen om det är heltal. 

 10* 15 = 150. man lägger till en nolla.

På samma sätt vet du hur man delar med 10 osv. 

 3700 / 100 = 37. Ta bort nollor.

Om det är decimaltal så flyttar du decimaltecknet. 

 10 * 37,5 = 375
 37,5 / 10 = 3,75

Räkna själv. MatteDirekt år 7, sid 16-17.

Men vad händer om du multiplicerar eller dividerar med 0,1 0,01 eller 0,001?

Det ser du på bilden till vänster.

Mål över G: Multiplikation och division med 0,1, 0,01, 0,001

  • Läsanvisning: Tetra B sid 8-11 (Stencil)

Datorövning. Multiplicera och dividera med 10, 100, 1000

Lektion 6 - Enheter

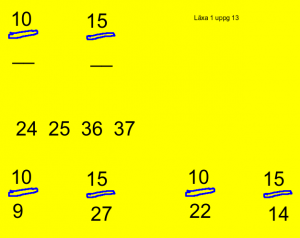
Uppföljning till läxa 1. Diskutera uppgifterna 6b och 13 på tavlan. Du ser dem här bredvid.

Längdenheter

Fundera på omdu kan alla dessa omvandlingar. 

 1 m = 10 dm = 100 cm = 1 000 mm = 1 000 000 mikrometer
 0,001 m = 1 mm  |  0,01 m = 1 cm  |  0,1 m = 1 dm
 1 km = 1000 m   |  10 km = 1 mil

Konvertera.nu

Titta på denna sida och svara på frågorna: konvertera.nu

Klicka på länken Volym. Välj sedan Signifikanta siffror 1. Då blir det en decimal. Testa att skriva 1 på liter och klicka utanför rutorna.

  1. Volym: Hur många centiliter går det på en liter?
  2. Volym. Hur många ml är en kubikcentimeter?
  3. Längd. Hur många meter är 1,2 km?
  4. Längd. Hur många nanomater går det på en mikrometer?

SI-enheter på wikipedia

Räkna själv:

Lektion 7 - Avrundning

Enkelt uttryckt. 1,2,3,4 avrundas nedåt. 6, 7, 8, 9 avrundas uppåt. numera avrundas femman uppåt men när jag lärde mig matte fanns det en krångligare regel så därför händer det att jag tvekar på detta. Så djupt sitter det man drillats i.

Mål: Kunna avrunda heltal och decimaltal

Datorövning från Matteva. Avrundning

  • MatteDirekt år 7, sid 10.
  • Matematikboken X sid 19-20 (stencil).

Lektion 8 - Överslagsräkning

Mål: Överslagsräkning

Gemensam övning

Räkna själv

  • Röd kurs sidorna 34-35 i matteDirekt.
  • (Matematikboken X sid 21-25 (stencil i pärmen).)

Datorövning. Matteva - uppskattning

Lektion 9 - Faktorisering

Genomgång läxa 3: uppgifterna 6B ? och 10.

Mål: Kunna faktorisera tvåsiffriga tal.


  • Memoryspel för att öva på att känna igen faktoriseringar. Memory kan säkert användas till en mängd övningar. I detta fall har jag gjort mallen i ppt där man printar åhörarkopior med sex bilder per sida. Varje bild är ett kort som man kan klippa ut och plasta in.
  • Uppgift. Du ska hitta på en matteuppgift. Den ska vara av typen - faktorisera talet xx. Du ska bestämma vad xx är för ett tal. Gör uppgiften svår genom att hitta på ett klurigt xx-tal. Alltså, hitta på det svåraste talet mellan 1-100 att faktorisera. Testa det på en kompis.

Datorövninga från matteva. http://www.skolresurs.fi/matteva/taluppfattning/faktorisering.html Faktorisering

Utmaning: spela 21

Lektion 10 Primtal

Mål: Veta vad ett primtal är och hur man undersöker om ett tal är ett primtal.

  • Spela Kenken. Där inser du att det kan vara bra att lära sig faktorisering.
  • MatteDirekt år 7 sid 38-39.
  • Hitta-primtalsspel med tärningar vilket jag kallat kryssa fullt. Poängen med spelet är att ....som vi förstår att ... vill inte avslöja mer.
  • Wikipedia förkarar Eratosthenes såll och jag lade till några uppgifter.
  • Matte Direkt sidan 41 om Eratosthenes beräkning av jordradien.
  • Pröva gärna att använda Excel för att undersöka om ett tal är ett primtal.

Datorövning. Lär dig mer om ett tal genom WolframAlpha. Du ser bland annat hur talet delas upp i faktorer. Skriv bara talet på raden och klicka enter.

Datorövninga från matteva. Delbarhetsreglerna

  • Här kan det vara bra att känna till att:
Ett helt tal är delbart med
2, 	om sista siffran (entalet) är jämt eller 0.
3, 	om talets siffersumma är delbar med 3.
4, 	om det tal, som bildas av de två sista siffrorna är delbart med 4.
5, 	när sista siffran är 0 eller 5.
6, 	när villkoren för 2 och 3 både är uppfyllda.
7, 	när talets tiotal minus dubbla antalet av talets ental är delbart med 7.
           Ex.:392 är delbart med 7 (39-4=35)
8, 	när det tal, som bildas av de tre sista siffrorna är delbart med 8.
9, 	när talets siffersumma är delbar med 9.
10, 	när talets sista siffra är en nolla.

Denna lista kommer från denna sida

  • Matte Direkt sidan 41, magiska kvadrater.
  • Matte Direkt sidan 43, fattiga, rika och perfekta tal.
Hämtad från ”https://wikiskola.se/index.php?title=Tal_och_räkning&oldid=13065”