Begreppet polynom

Teori

Definition
Polynom Ett polynom består av termer. Termerna innehåller variabler med koefficienter framför. Variablerna kan ha en exponent som är ett heltal. Den största exponenten anger polynomets grad. Exponenten noll innebär en konstantterm.

Exempel på polynom

Benämning	Exempel
Nolltegradspolynom	[math]\displaystyle{ 1 }[/math]
Förstagradspolynom	[math]\displaystyle{ 2x+1 }[/math]
Andragradspolynom	[math]\displaystyle{ x^2+2x+1 }[/math]
Tredjegradspolynom	[math]\displaystyle{ 4x^3+3x^2+2x+1 }[/math]
Fjärdegradspolynom	[math]\displaystyle{ 5x^4+4x^3+3x^2+2x+1 }[/math]

Exempel

[math]\displaystyle{ 3 x^3 + 4 x^2 - 2 x - 7 }[/math] är allts¨ett polynom av grad 3. Eftersom alla exponenter upp till 3 finns representerade bland termerna kallas polynomet fullständigt. Om en term med någon exponent saknas kallas polynomet ofullständigt. En polynomfunktion kan skrivas: [math]\displaystyle{ f(x) = 2 x^2 +3 x - 7 }[/math] Polynomfunktinen har ett värde som korresponderar mot ett värde på varibaln. Exempelvis har funktionen ovan värdet [math]\displaystyle{ f(2) = 7 }[/math]

Faktorisering och nollproduktsmetoden

Nu vet vi att x-värden för punkterna där andragradfunktinens graf skär x-axeln motsvara lösningen till ekvationen där funktionen är lika med noll, f(x) = 0. Dessa x-värden kallas nollställen.

Ett annat sätt att hitta nollställena är att faktorisera andragradsfunktionens uttryck. Nollproduktssatsne säger då att om a b = 0 så är antingen a = 0 eller b = 0. Genom att faktorisera andragradsfunktionen fås ett uttryck på formen k (x-a) (x-b) = 0. Nollställena x = a och x = b utgör då lösningar (rötter) till ekvationen.

Definition
Nollställe En punkt i en funktions definitionsmängd där funktionens värde är noll Besläktade ord: nollställa. Nollställena i en andragradsfunktion befinner sig på samma avstånd från symmetrilinjen.

Förenkling av rationella uttryck

Det här kommer vi att gå djupare in på under nästa lektion.

Exempel
Förenkla uttrycket: [math]\displaystyle{ \frac{x^2-8x+16}{x-4} }[/math] Vi börjar med att faktorisera täljaren: [math]\displaystyle{ \frac{(x-4)(x-4)}{x-4} }[/math] Och nu kan vi förkorta med x-4 i täljare och nämnare och får det förenklade uttrycket: [math]\displaystyle{ x-4 }[/math]

Uppdelning i faktorer med konjugatregeln

Vi gör nedanståendde övningar på kortast möjliga tid för att få upp tempo och automatisera procedurerna.

Exempel
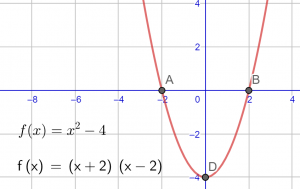
Faktorisera för att hitta nollställena Vilka rötter har ekvationen [math]\displaystyle{ x^2 - 6 x + 9 }[/math] ? Faktorisering ger (x-3)(x-3) = 0 vilket innebär att x = 3 är ett nollställe och en dubbelrot. Ekvationen kan även skrivas på formen [math]\displaystyle{ (x-3)^2 = 0 }[/math]

Uppgift

Först ska vi repetera konjugatregeln med ett lösblad där det är rad snabba uppgifter. Dessa uppgifter bör klaras av på mindre än tre minuter. Sedan testar vi om du kan använda konjugatregeln baklänges. Dela upp följande uttryck i faktorer: [math]\displaystyle{ x^2 - 9 }[/math] [math]\displaystyle{ x^2 - 81 }[/math] [math]\displaystyle{ c^2 - 4 }[/math] [math]\displaystyle{ x^2 - 6 }[/math] [math]\displaystyle{ x^2 - 3.4 }[/math] [math]\displaystyle{ x^2 - k^2 }[/math]

Uppdelning i faktorer med kvadreringsreglerna

Uppgift
Här ska vi också repetera kvadreringsreglerna med ett lösblad. Du ska även kunna kvadreringsreglerna baklänges. Exempel: 1+2x+x2 = (1+x)2 Testa nu om du kan kvadratern med kvadreingsregeln baklänges! 4+8x+4x2= 4-12x+9x2= 64+144x+81x2= 0.25-10x+100x2= a2-2ab+b2= a2+2abx+b2x2= 0.16a2+2.4ax+9x2= 9y2-12x2y+4x4=

Uppdelning i faktorer utan konjugat- eller kvadreringsreglerna

Det är ofta lätt att hur ett polynom av andra graden (andragradsfunktion) kan faktoriseras med hjälp av konjugat- eller kvadreringsreglerna men det går att faktorisera många andra polynom av andra graden men ekvationens form blir då [math]\displaystyle{ (x-a)(x-b) = 0 }[/math] och rötterna är a respektive b. Det motsvara fallen då andragradsfunktionen inte är symmetrisk med y-axeln.

Exempel
Ekvationen [math]\displaystyle{ x^2 -x -6 = 0 }[/math] kan skrivas som [math]\displaystyle{ (x+2)(x-3) = 0 }[/math] Rötterna är : [math]\displaystyle{ x= -2 }[/math] och [math]\displaystyle{ x=3 }[/math] Observera den negativa roten. Faktorn : [math]\displaystyle{ (x+2) = 0 }[/math] om [math]\displaystyle{ x= -2 }[/math]

Lär mer

Öva procedurer

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Polynom, skrivsättet, av Åke Dahllöf

Här kan man öva på att hitta faktorerna även om det inte går att använda kvadrerings- eller konjugatregeln. Använd hint-funktionen om du behöver hjälp.

Repetition av Ma2c

Mycket av detta bygger på avsnittet Nollställe i Ma2c.

Matematisk relevans

Uppgift
Vad kan man ha faktoriseringen till inom matematiken? Metoden att faktorisera kan fungera som komplement till en annan känd teknik som vi använder på andragradsfunktioner. Tag fram en tydlig beskrivning av hur man faktoriserar andragradspolynom utan att använda konjugat- eller kvadreringsreglerna.

Exit Card

Exit Card - Kvadrerings- och konjugatreglerna baklänges