Enhetscirkeln: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) (Skapade sidan med ' {{lm3c|Enhetscirkeln|16-21}} {{clear}} {{#ev:youtube| P9ZWjEkHVrk |240|left|Enhetscirkeln intro}}{{#ev:youtube| FoHkqQFiqP8 |240|right|Enhetscirkeln del 2}} {{#ev:youtube| M...') |
Hakan (diskussion | bidrag) |
||
| Rad 25: | Rad 25: | ||
<iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/79980/width/1366/height/558/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/auto" width="1366px" height="558px" style="border:0px;"> </iframe> | <iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/79980/width/1366/height/558/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/auto" width="1366px" height="558px" style="border:0px;"> </iframe> | ||
</html> | </html> | ||
=== [[Fördjupning - Enhetscirkeln]] === | === [[Fördjupning - Enhetscirkeln]] === | ||
Versionen från 1 mars 2019 kl. 20.47
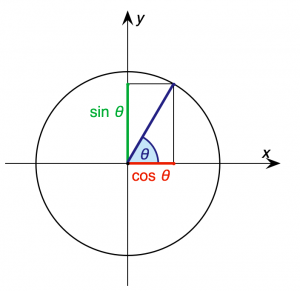
Dagens lektion handlar om trigonometri och cirklar. genom att titta på enhetscirkeln går vi utanför den rätvinkliga triangeln och kan arbeta med vinklar större än 90°. Genom att enhetscirklen har radien ett blir hypotenusan 1.
| Definition |
|---|
Sinus och kosings i enhetscirkeln
|
Viktiga samband
| Definition |
|---|
Speglingar i x-axeln och y-axeln
|

