Exponentialekvationer: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 18: | Rad 18: | ||
=== Grafisk löning === | === Grafisk löning === | ||
=== Exempel 1 === | |||
Bestäm exponentialfunktionen där grafen går genom punkterna (0,2) och (5,6) | |||
# Sätt in x = 0 så får du C | |||
# Sätt in x = 5 och y = 6 i funktionen och räkna ut a | |||
{{uppgruta | Lös upppgiften ovan med GeoGebra | |||
Skriv in funktionen y {{=}} C a <top>x<\top> | |||
Du kommer då att få frågan om du vill skapa glidare för C och a. Det vill du. | |||
Dsa i glidarna och finn lösningen. | |||
}} | |||
=== Exempel 2 === | |||
Lös ekvationen 2<sup>x</sup> = 1 + 3x grafiskt. | |||
Lös även olikheten 2<sup>x</sup> < 1 + 3x | |||
==== Vatten i termos ==== | ==== Vatten i termos ==== | ||
Versionen från 14 februari 2018 kl. 15.28
|
|
Teori
| Definition |
|---|
|
Grafisk löning
Exempel 1
Bestäm exponentialfunktionen där grafen går genom punkterna (0,2) och (5,6)
- Sätt in x = 0 så får du C
- Sätt in x = 5 och y = 6 i funktionen och räkna ut a
| Uppgift |
|---|
| Lös upppgiften ovan med GeoGebra
Skriv in funktionen y = C a <top>x<\top> Du kommer då att få frågan om du vill skapa glidare för C och a. Det vill du. Dsa i glidarna och finn lösningen. |
Exempel 2
Lös ekvationen 2x = 1 + 3x grafiskt.
Lös även olikheten 2x < 1 + 3x
Vatten i termos
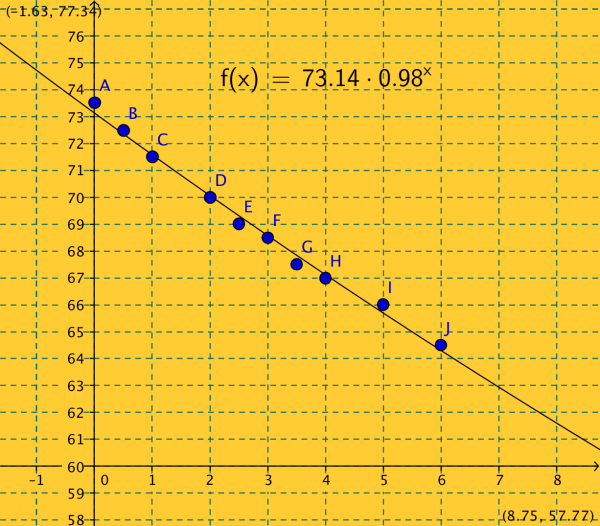
Figuren nedan visar temperaturen hos vatten som får svalna i en termos. Mätvärdena har lagts i en lista som heter avsvalning i GeoGebra. Därefter har kommandot RegressionExp[avsvalning] använts för att anpassa en exponentiell funktion till värdena i listan.
Du ser på funktionen f(x) att basen är 0.98 (= förändringsfaktorn)
Logaritmera ekvationer
Dessa och liknade ekvationer löser man genom att logaritmera båda sidorna.
Varför är det så?
Om 102a+3b = 10y så innebär det att 2a+3b = y
Om log(2a+3b) = log y så innebär det att 2a+3b = y
Om log 10x = log 27 så innebär det att 10x = 27
Om man går åt andra hållet kan man säga att om 10x = 27 så innebär det att log 10x = log 27
Nu har vi hittat en metod att lösa ekvationer med exponentialfunktioner. Den kallas att logaritmera.
Exempel
Lös ekvationen 102x = 200
Logaritmering av båda sidorna ger
log 102x = log 200
2x = log 200
x = log (200) /2
Aktivitet
| Uppgift |
|---|
Lös verkliga problem
|

