Problemlösning exponentialfunktioner: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 19: | Rad 19: | ||
<br /> | <br /> | ||
[http://www.edusci.umu.se/np/np-2-4/tidigare-givna-prov/ Nationellt prov ma3c ht 2012.] | [http://www.edusci.umu.se/np/np-2-4/tidigare-givna-prov/ Nationellt prov ma3c ht 2012.] | ||
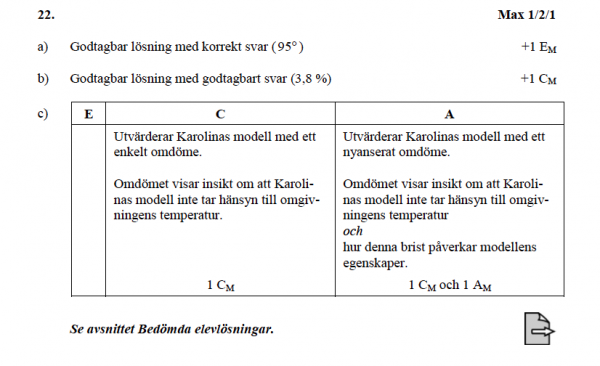
| [[Fil:NpMa3c ht 2012 Del D uppgift 22 - facit.png|vänster| | | [[Fil:NpMa3c ht 2012 Del D uppgift 22 - facit.png|vänster|600px |Facit]] | ||
}} | }} | ||
Versionen från 18 april 2016 kl. 08.40
| Definition |
|---|
Problemlösning med exponentialfunktionen - Vad kan man fråga efter?
|
Ett problemlösningsexempel
Facit: (klicka expandera till höger)
Ett exempel med flera modeller
Man häller kaffe i en termos. Kaffet har från början temperaturen 92° C. Termosen ställs sedan i ett rum där temperaturen är 15° C. Temperaturen antas förändras enligt någon av dessa tre modeller:
- a) [math]\displaystyle{ y(t) = 92 - 7 t }[/math], där t är tiden i timmar.
- b) [math]\displaystyle{ y(t) = 92 \cdot 0.93^t }[/math]
- b) [math]\displaystyle{ y(t) = 15 + 92 \cdot e^{-0.025 t} }[/math]
Ta reda på under vilka tider modell a, b respektive c gäller.
Resonera om vilken modell som är bäst.
GeoGebra med modellerna
Läs gärna mer vad Wikipedia skriver om Newtons_avsvalningslag