Geometri 2C: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 2: | Rad 2: | ||
[[File:Animated construction of Sierpinski Triangle.gif|400px|right|Animated construction of Sierpinski Triangle]] | [[File:Animated construction of Sierpinski Triangle.gif|400px|right|Animated construction of Sierpinski Triangle]] | ||
<html><script id="WolframAlphaScript" src="http://www.wolframalpha.com/input/embed/?type=small" type="text/javascript"></script></html> | <html><script id="WolframAlphaScript" src="http://www.wolframalpha.com/input/embed/?type=small" type="text/javascript"></script></html> | ||
=== [[En elevuppgift att skapa lektionsbeskrivningar i matematik]] === | |||
Den här övningen körde vi 2012 och skapade på så sätt mycket av detta innehåll | |||
== [[Beräkning av vinklar]] == | == [[Beräkning av vinklar]] == | ||
| Rad 15: | Rad 19: | ||
== [[Bisektrissatsen och kordasatsen]] == | == [[Bisektrissatsen och kordasatsen]] == | ||
== Likformighet och kongruens == | == Likformighet och kongruens == | ||
Versionen från 28 september 2016 kl. 10.03
<facelikebutton style="2" showsend="0"></facelikebutton>

En elevuppgift att skapa lektionsbeskrivningar i matematik
Den här övningen körde vi 2012 och skapade på så sätt mycket av detta innehåll
Beräkning av vinklar
Likformighet och kongruens
Längd-, area- och volymskala
Topptriangelsatsen och transversalsatsen
Randvinklar och medelpunktsvinklar
Bisektrissatsen och kordasatsen
Likformighet och kongruens
s. 71 -74
Khan Academy: likformiga trianglar
Likformighet

Definition
Likfromighet är två objekter som har exakt samma form, men är inte lika stora (se bild ⇒⇒).
Två trianglar är likformiga om något av följande är uppfyllt:
VVV: Motsvarande vinklar är lika. SSS: Förhållandet mellan de tre sidparen är lika SVS: Förhållandet mellan två sidpar är lika och mellanliggande vinkel är samma
Video
Exempel (Uppgift)
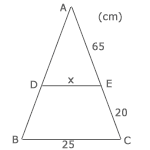
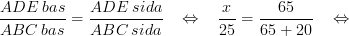
ADE bas/ABC bas betyder att vi tar måtten på sträcken DE från den lilla triangeln och dela den med måtten på sträcken BC från den stora triangeln samt ADE sida/ABC sida betyder att vi tar måtten på sträcken AE från den lilla triangeln och dela den med sträcken AC från den stora triangeln, och det blir alltså summan på AE och EC. Man kan också använda formeln genom att dela den stora triangeln med den lilla istället, och svaret blir detsamma.
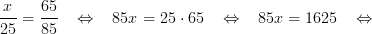
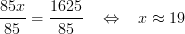
Användningsområden
Man kan tex. använda likformighet i avbildningar när man ska rita kartor och jorden på olika skalor, dvs. 1:2, exempelvis:-
Hund i längdskala 1:1
Hund i längdskala 1:2. Areaskalan är 1:4
Länkar
Likformighet GeoGebra
Topptriangelsatsen
Den här filmen handlar om likformighet och topptriangelsatsen. Observera att sidan som är 15 lång i exemplet gäller sidan på hela den stora triangeln.
Kongruens
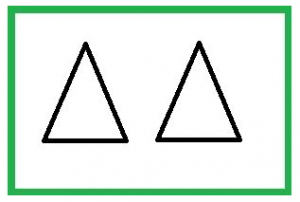
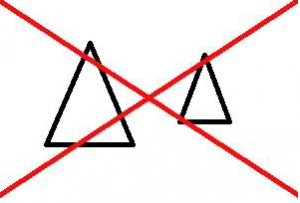
| Definition |
|---|
| Kongruens
Två figurer är kongruenta om de har samma form och samma storlek. Två trianglar är kongruenta om något av följande tre fall gäller:
|
Länkar
Bilder
Extrauppgift på kul
| Uppgift |
|---|
| Kan du rita en regelbunden hexagon med hjälp av Geogebra?
 |
Längd, area och volymskala
Förra veckodiagnosen ?
s. 75- 79
Tisdag v 8.
Håkans tips
- klippa in en svg-bild fr Wikipedias source
Definition
Skala = En sträcka i bilden / Motsvarande sträcka i verkligheten
Definition: Längdskala
Längdskala = Bildens längd / Motsvarande längd i verkligheten
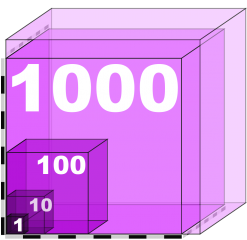
Definition: Areaskala
Areaskala = Stor kvadratens area / Lilla kvadratens area
Definition: Volymskala
Volymskala = Stora kubens volym / Lilla kubens volym
Länkar
- Scale of the Universe (Flash animation)
- Skala på Wikipedia
- Längdskala och areaskala - Matteboken.se
- Skala och likformighet - Matteguiden.se
ViktorE Skala
Topptriangel- och transversalsatsen


Wikipedia skriver om Topptriangelsatsen Wikipedia skriver om Transversalsatsen
Det finns en PPT som förklararar dessa satser och ur de hänger ihop: http://wikiskola.se/index.php?title=Fil:Likformigheter_och_transversaler.pptx . Det är en kort ppt så dess bilder finns med här.
NilsG Topptriangelsatsen
MalinC Brättar om topptriangelsatsen
Transversalsatsen
Euklidiskt bevis av Transversalsatsen
| Uppgift |
|---|
| Bevisa Transversalsatsen
Gå till sidan MalinC om Transversalsatsen och följ hennes instruktion om hur du bevisar transversalsatsen. här får du göra det "Euklidiska" beviset som bygger på jämförande av areor. Detta är en uppgift på C-A-nivå |
Randvinklar och medelpunktsvinklar
86-91
Onsdag v 8.
Vi har en kort lektion för tre tunga geometriska satser. Så ser grovplaneringen ut och vi måste komma vidare till avsnittet om räta linjen. Det säger sig självt att vi kommer att behandla detta översiktligt (inte så noga alltså). men vi kommer att repetera detta när ni har lagt in ert material. Ni kommer inte undan er uppgift att skriva på wikiskola för det där med att kommunicera matematik är ett viktigt grundmaål.
Även om dessa satser är intressanta är det inte centrala. titta på beskrivningen av det cerntrala innehållet i geometrin:
Användning av grundläggande klassiska satser i geometri om likformighet, kongruens och vinklar.
Med klassiska satser om vinklar menas förmodligen vinkelsumman och yttervinkelsatsen tillsammans med begreppen sidovinklar, vertikalvinklar och alternatvinklar (och transversalen). Jag ska titta i en annan bok hur de tolkar kursplanen.
Nåväl, något måste vi göra och min idé är att vi tar GeoGebra och konstruerar alla tre geometriska figurer och sätter oss in i vad de betyder på detta sätt. På det viset kommer vi att prata om och jobba med begreppen och det ökar chansen att vi blir bekanta med varandra.
Håkans tips
- bädda in youtube. Det kan vi göra med Nils film ovan.
Extramatten
Extramatten idag handlar om att repetera inför omprovet
Randvinkelsatsen

Här kommer ett riktigt bra bevis av randvinkelsatsen:
Och därefter kommer en film med Kahn:
Ett uppgift på Khanacademy för Randvinkelsatsenm
Håkans GeoGebra om randvinkelsatsen
Öva
Bisektrissatsen
Länkar
Text om Bisektrissatsen.....
Defenition...
Bisektrissatsen = AD / BD = AC / BC
AntonL - Kordasatsen
Antons hittade film:
Gammal diagnos
| Uppgift |
|---|
| Gör denna gamla diagnos |
Repetition och sammanfattning av geometrin
Diagnos 1 geometri Ma2C är en Geogebra som innehåller likformighet, transversalsatsen, randvinkelsatsen, kordasatsen och bisektrissatsen på ett och samma ställe. Jag använder den för att skapa enkla diagnoser. Det är bara att ändra litet i figurerna så blir et nya versioner av diagnosen.
olleh: http://olleh.se/start/frageprogramMa2.php
MalinC: http://www.malinc.se/math/geometry/circles_angles_proofssv.php



