Exponentialekvationer

Teori

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Exempel på exponentialekvationer

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Logaritmer med olika baser, av Andreas Borg

Skillnaden funktion - ekvation

Vilken är egentiligen skillnaden mellan en exponentialfunktion och en exponentialekvation?

Exponentialfunktionen har ett y-värde som korresponderar till ett x-värde. Den är kontinuerlig och definitionsmängden respektive värdemängden utgörs av de reella talen.

Om exponentialfunktionen sätts lika med ett värde eller en annan funktion får vi en exponentialekvation. Grafiskt är lösningen skärningspunkten mellan de två graferna, den för exponentialfunktionen och den för den andra funktionen (y = konstant eller vilken funktion som nu representerar högerledet i ekvationen).

Definition
[math]\displaystyle{ f(x) = C \cdot a^{x} }[/math] är en exponentialfunktion [math]\displaystyle{ C \cdot a^{x} = B }[/math] är en exponentialekvation

Exponentialfunktionerna kan skrivas på flera former, exempelvis

• [math]\displaystyle{ f(x) = C \cdot e^{kx} }[/math]
• [math]\displaystyle{ f(x) = C \cdot a^{x} }[/math]
• [math]\displaystyle{ f(x) = e^{kx + a} }[/math]

Exempel

Exponentialfunktioner är en klass av matematiska funktioner som kännetecknas av att funktionsvärdets ändringstakt är proportionell mot funktionsvärdet. Exempelvis kan ränta på ränta beräknas som [math]\displaystyle{ slutbeloppet = r^x\cdot startbeloppet }[/math] där [math]\displaystyle{ r^x }[/math] är en exponentialfunktion, den årliga räntefaktorn är r (till exempel 1,10 för 10 % ränta) och x antalet år.

Metod - Logaritmera ekvationer

Dessa och liknade ekvationer löser man genom att logaritmera båda sidorna.

Varför är det så?

Om [math]\displaystyle{ 10^{2a+3b} = 10^y }[/math] så innebär det att [math]\displaystyle{ 2a+3b = y }[/math]

Om [math]\displaystyle{ log(2a+3b) = log y }[/math] så innebär det att [math]\displaystyle{ 2a+3b = y }[/math]

Om [math]\displaystyle{ log 10^x = log 27 }[/math] så innebär det att [math]\displaystyle{ 10^x = 27 }[/math]

Om man går åt andra hållet kan man säga att om 10^x = 27 så innebär det att

[math]\displaystyle{ log 10^x = log 27 \quad }[/math] och då är ju enligt logaritmlagarna

[math]\displaystyle{ x\cdot log 10 = log 27 \quad }[/math] och

[math]\displaystyle{ x = log 27 }[/math]

Nu har vi hittat en metod att lösa ekvationer med exponentialfunktioner. Den kallas att logaritmera.

Exempel

Exempel
Lös ekvationen [math]\displaystyle{ 10^{2x} = 200 }[/math] Logaritmering av båda sidorna ger: [math]\displaystyle{ log 10^{2x} = log 200 }[/math] [math]\displaystyle{ 2x = log{200} }[/math] [math]\displaystyle{ x = log (200) /2 }[/math]

Aktivitet

Uppgift
{{{1}}}

Laboration - Kaffe i termos

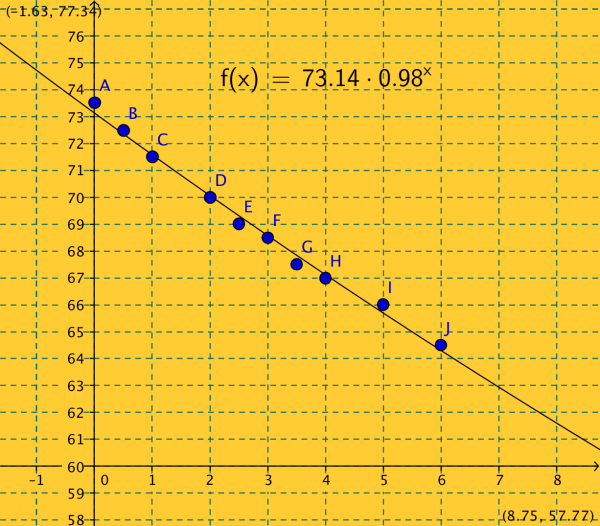
Figuren nedan visar temperaturen hos vatten som får svalna i en termos. Mätvärdena har lagts i en lista som heter avsvalning i GeoGebra. Därefter har kommandot RegressionExp[avsvalning] använts för att anpassa en exponentiell funktion till värdena i listan.

Du ser på funktionen f(x) att basen är 0.98 (= förändringsfaktorn)

Uppgift
Ett praktiskt experiment Skaffa en termomenter avnågot slag och brygg en het kopp kaffe. Mät temperaturen vid minst fem tidpunkter. Gör en kurvanpassning enligt ovan. Vilken exponentialfunktion får du?

Lär mer

Hitta funktionen grafiskt med GeoGebra

Uppgift

Bestäm funktionen algebraiskt eller med GeoGebra Bestäm exponentialfunktionen [math]\displaystyle{ y = C a^x }[/math] där grafen går genom punkterna (0,2) och (5,6) Algebraiskt Du behöver beräkan a och C. Sätt in [math]\displaystyle{ x = 0 }[/math] så får du C Sätt in [math]\displaystyle{ x = 5 }[/math] och [math]\displaystyle{ y = 6 }[/math] i funktionen och räkna ut a Grafiskt Skriv in funktionen [math]\displaystyle{ y = C a^x }[/math] Du kommer då att få frågan om du vill skapa glidare för C och a. Det vill du. Dra i glidarna och finn lösningen.