Multiplikation och division i polär form

Repetition

[math]\displaystyle{ cos (u+v) = \cos u \cos v - \sin u \sin v }[/math]

[math]\displaystyle{ sin (u+v) = \sin u \cos v + \cos u \sin v }[/math]

[math]\displaystyle{ cos (u-v) = cos u cos v + sin u sin v }[/math]

[math]\displaystyle{ sin (u-v) = sin u cos v - cos u sin v }[/math]

Vi kommer använda:

[math]\displaystyle{ \cos (u+v) = \cos u \cos v - \sin u \sin v }[/math]

[math]\displaystyle{ \sin (u+v) = \sin u \cos v + \cos u \sin v }[/math]

Två komplexa tal

[math]\displaystyle{ z = r (\cos u + i \sin u) }[/math]

[math]\displaystyle{ w = s (\cos v + i \sin v) }[/math]

Då blir:

[math]\displaystyle{ z \cdot w = r (\cos u + i \sin u) \cdot s (\cos v + i \sin v) = }[/math]

[math]\displaystyle{ = r \cdot s (\cos u \cos v + i \cos u \sin v + i \sin u \cos v + i^2 \sin u sin v) = }[/math]

[math]\displaystyle{ = r s ((\cos u \cos v - \sin u \sin v ) + i (\cos u \sin v + \sin u \cos v )) = }[/math]

[math]\displaystyle{ = r s ( cos (u+v) + i \sin (u+v) ) }[/math]

Det innebär alltså att vid multiplikation av komplexa tal så multipliceras absolutbeloppen och adderas argumenten.

Vid division av två komplexa tal dividerar men längderna på vektorerna:

[math]\displaystyle{ | \frac{z}{w} | = \frac{|z|}{|w|} }[/math]

I analogi med multiplikationen så ska man subtrahera argumenten vid division av komplexa tal:

[math]\displaystyle{ arg \frac{z}{w} = arg z - arg w }[/math]

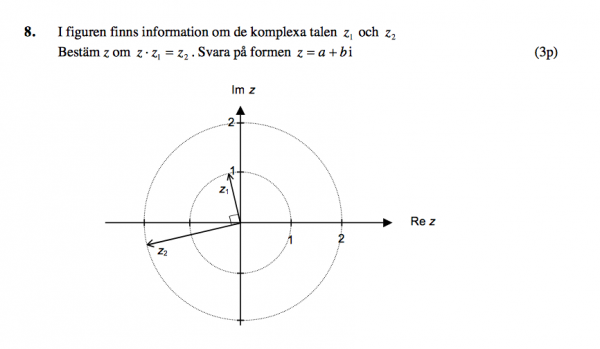
Uppgiften från Provbanken.