Funktioner 2C

Funktion och graf

Celler de Sant Cugat lateral

s 146

Teori funktionen f(x)

Vad står f(x) för? Funktionen f med variabeln x.

Lösa ekvationer med grafer

Definitionsmängd = x-värdena

Värdemängd = y-värdena

Andragradsfunktioner

Fyra sätt att beskriva andragradaren

Vi kommer att arbeta med fyra representationer, fyra sätt att beskriva andragradsfunktionen. Alla sätt beskrivs mer ingående senare men här kommer en snabb sammanställning i några rader och eventuell bild.

Generell algebraisk form

Andragradsfunktionen på allmänn form [math]\displaystyle{ f(x) = ax^2 + bx + c }[/math].

Exempel: Andragradsfunktionen [math]\displaystyle{ f(x) = 2x^2 - 4 }[/math].

Vertex och nollställe

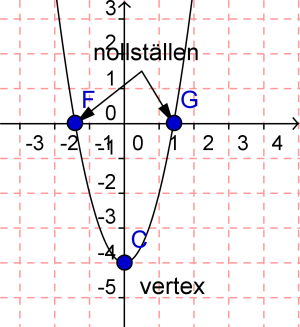
Varje parabel har en extrempunkt där den antar sitt högsta eller lägsta värde. Dessutom kan den ha ett eller två nollställen men det är inte alltid så.

Läs mer

Fokus och styrlinje

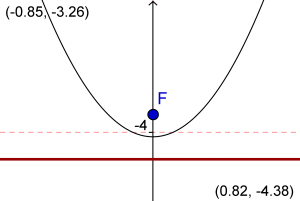
Andragradsfunktionen beskrivs och ritas upp utifrån en linje och en punkt.

Läs mer

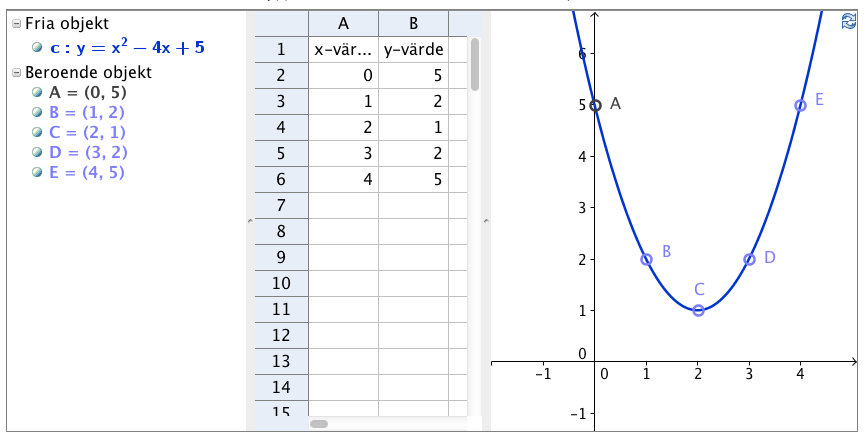
Värdetabell

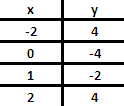
Som med alla funktioner kan man göra en värdetabell med x- och y-värden. När dessa talpar ritas in i ett koordinatsystem får man funktionens graf.

Läs mer

Parabelns ekvation

Avståndet till styrlinjen är lika med avståndet till fokus

Definitioner

Brännpunkt kallas också fokus

Styrlinje är en linje som används för att konstruera parabeln

GeoGebra som visar samma avstånd

En punkt på andragradsfunktionens graf har samma avstånd till styrlinjen som till fokuspunkten. Testa genom att flytta punkten så får du se.

18 Maj 2013, Skapat med GeoGebra

Parabelns egenskaper i GeoGebra 1

Du kan lära dig litet om hur parabeln fungerar och vad den har för egenskaper med denna övning:

Datorövning: Malin C GGB-övning

GeoGebra med styrlinje och fokus

Den här andragradsfunktionen har konstruerats med en styrlinje och en fokkuspunkt. Du kan undersöka hur funktionens utseende förändras när du flyttar fokuspunkten genom att dra i glidarna för a och b.

Du kan skapa en lika dan andragradsfunktion i GGB med kommandot:

Parabel[ <Punkt>, <Linje> ]

<ggb_applet width="792" height="319" version="4.0" ggbBase64="UEsDBBQACAAIACI+i0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAiPotAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1YW2/bNhR+bn/FgZ42ILZFSZTswm6RFihWIO0KpBuGvVESY7ORRE2kbTnoj98hKclyLkWSDkOBurwdnst3blSWb9qygB1vlJDVyiNT3wNeZTIX1XrlbfXVZO69ef1yueZyzdOGwZVsSqZXXmQoRb7yeHRFgyiYT/J4wScRZYtJms8Xk5DmPA+veJgmmQfQKvGqkp9YyVXNMn6ZbXjJLmTGtBW80bp+NZvt9/tpL2oqm/VsvU6nrco9QDUrtfK6yStkd3JpH1rywPfJ7K+PF479RFRKsyrjHhgTtuL1yxfLvahyuYe9yPVm5c19NGPDxXpjbKKRBzNDVCMgNc+02HGFV0dLa7Mua8+Sscqcv3AzKAZzPMjFTuS8WXn+NKAeyEbwSnenpJMy6+8vd4LvHSMzszJQFS1lkTLDA759g8APfDgzA3FDgEMcuyPf7fmhGwI3RG6gjiZy1yNHGjmayNFEoQc7oURa8JV3xQqFmInqqkF/DWulDwW3+nQbR3vJGdqkxA0ShwZRBzLu+/6Z+cX4i8zB7NRIMpKqm+0ThfYi6Tx5vMjgR0SGvcjgPisD+oCV8XfAdTo8xkxCRzJRlP1nf3ckhsETJLr1jwmMo//FxOWsz5RllxygNoa286TmpTLpEi6ALkzUE6CYGnGCQU6BLHBIAsBkAEIhorgkc4jNmECY4EEEIczB0JEQbG7QOf4XJZZZDBSZmd0EUxIICoqAhkBsSkWAiQQ2LTFFgxApKAWKl4x4EhgWYQxRjKtwDhHqaDIyIUgY4kVco/gAQgKhuUwSCGKIDT8SmUyP50Z1ZBlA7ENMDENMakxol8xIP4fQWBN3cImq3uoTiLIy76da1oMvkBrL0bHMufJ0UgVfLAuW8gIbw6XxJMCOFSYjrKArWWnonRi4vXXD6o3I1CXXGm8p+Mp27IJp3r5HatXLtrSZrNTnRup3stiWlQLIZOEPOsuCjObBoDUuwtFBND6go4N4NE/ulSvxBLaKo3zZqJ6c5fkHQ3EsDYjk71VxeNtwdl1LcWrGcmZ7zJJvs0LkglV/YrAaKQYX6FuOrVZ9ywl90isim/zyoDCCof2bNxJxTOJpnERJTJM4ChYRptjBnQSUTsnCX5AwoYsEuy92GJUxk3shmYbEj+eLBY0jGuNFvPXAWSea7wYPsZYPxq8bk9id4WbxQb2VxXHLmv+O1Xrb2McC1sbGGHVerQtuQ8QmNnbi7DqV7aWLjdDx+nKoceU7BdK1hR0aaxkSdGPqRktjNBuofEvjWwq/DzaRD+dkEVgKO6ZutFQYvU61zlLSm0n8XoxQtqD53kna2NA3fX1bCX3RL7TIro+WGvpP2zLlQwCdsiT/Ecvl7FaALa95U/Gii2f05FZulUvPUajnPBMlLt1BBwgzzvoDFXC7OV83vNe7sM8wB5c99cehemfbsnrfyPJDtfuCkXBLgeWs13KpskbUJuAgxR5wzY8xlQvFsIXk43smAdH0zLQKhEcbaDA1t3ojG/vSwoqCo8m7gpf4ygJtg8v4ekCZ2feagRNk+hVr2i0vjHDC83sDjVCMXVbUG2YedZ3RBTvw5gQGy/CjzG+Dg9hbCzDDa8PAeLfm3MWF7tIBamRos+mkRiHeClonFg7dM/1m5U3IoMcQ2BpL7jU+KzFg6Iixmfwm8pzbduvy/p/KXVEu3nhbFyITuosxB+YdWKttyRuRDcjh1dyCi+ZuO6PDaeREPAz4MT8ewtsfoU0eiXZHpwrz9oZSVJZNyRA7bIksVdheNH58YJBXx48Pp1hXnvEhZ9DFG2Ey7/GmiZldiZYP3ROjT9xgtrETY+71Q/B9Pzw/Nh7vpfYeL5Ee1p/ASxPauYk+3U3zIS0I+fnd1NYNSjNsOozf4hd3i/x+MT46A5NPv/bsbI91r7NT/3YHA4sfdaPtt88tbscCZULKeMIUAFOghvpk9TVPgJNXo9u91UnGaGWyLFmVQ2W/Iz6zhqWycLXcPW2ZbwFkxJR4Z+FW9weZY9cxuYMhNpZRhmTP6xD46fxANjwRxGdVcLHm1Q51xTcrQOv3HcLvW0Q/aUnXLOBAOqIbMnIPBnYjWjjv6c97qvPApNU0wSfrOT61J24zstzQ1ef4yp4EfbW/3VBEeX9DmY1bun02d3/yef0vUEsHCPX7kV9KBgAAjxIAAFBLAQIUABQACAAIACI+i0BFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAIj6LQPX7kV9KBgAAjxIAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADiBgAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true"/>

Övning - hitta funktionen om du vet fokus och styrlinje

Övningsuppgift: hitta funktionen

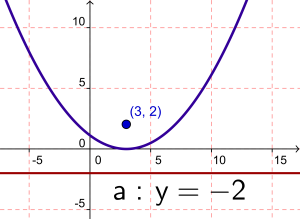
Detta är en viktig uppgift. Se även Exemplet på sid 152 i Matematik 2C.

Den här uppgiften utgår ifrån att du vet styrlinjen och fokuspunkten men ska ta fram funktionen. Se figuren till höger.

1. Börja med att markera en punkt (x,y) på grafen i första kvadranten.
2. Skriv ett uttryck för avståndet från (x, y) till linjen.
3. Skriv ett uttryck för avståndet från (x, y) fokus.
4. Det gäller för en parabel att avståndet från (x, y) till fokus är samma som avståndet från (x, y) till linjen. Visa detta genom att sätta de två uttrycken lika.
5. Lös ut y ur ekvationen ovan. Det gör du genom att kvadrera båda sidorna så att roten går bort. Du behöver utveckla kvadraterna med hjälp av kvadreringsregeln.

Nu är du klar. Ekvationen du fick beskriver parabeln.

Andragradsfunktionens graf

Begrepp och egenskaper hos andragradsfunktionern

vertex är kurvans vändpunkt

nollställen

positivt före x²-termen betyder minimipunkt

negativt före x²-termen betyder maximipunkt

symmetrilinje genom vertex

Hur ritar man en parabel om man vet funktionen?

Man gör en värde tabell. Tag ett lämpligt x-värde och skriv i tabellens x-kolumn. Räkna ut vad y blir genom att sätta in x-värdet i funktion. Skriv y-värdet i dess kolumn. Nu har du det första talparet. Upprepa med ett antal lämpliga x-värden tills du fått minst tre gärna fem talpar. Det är viktigt att du väljer talparen så att du hittar vertex (min- eller maxpunkten).

Om du har funktionen i den allmänna formen y(x) = ax² + bx + c kan det vara bra att kvadratkomplettera.

Fördjupning

Det kan vara intressant att som bakgrund titta på denna sida om kägelsnitt.

Testa dina kunskaper om andragradsfunktioner

Uppgift
Gör denna diagnos på ekvationssystem Veckodiagnos 19 om andragradsfunktioner Veckodiagnos 21 om andragradsfunktioners egenskaper

Digitala rutan

Sidan 159.

Gör den i GeoGebra.

Kvadratiska modeller

Square root

Så här ser andragradsfunktionen ut på allmän form:

y(x) = ax² + bx + c

c anger var grafen skär y-axeln. a gör bland annat parabeln smalare eller bredare. bx-termen ger en diagonal förflyttning av hela kurvan (något förenklat uttryckt).

Exempel 1

ParabolicWaterTrajectory

Exempel 1 handlar om att man har en måttsatt bild och ska anpassa den allmänna funktionen y(x) = ax² + bx + c till dessa mått.

Här är det smart att placera origo symmetriskt i bilden och att kika på ställena där grafen skär x-axeln och där den skär y-axeln.

Övning 1 - Skapa parabelns funktion utifrån en bild med mått

Anpassa den allmänna funktionen till vattenstrålen i bilden. Strålen når 2 m långt och är 1.5 m hög.

Övning 2 - Skapa parabelns funktion utifrån vertex och nollställen

Detta är en viktig uppgift. Se även Exempel 1 på sid 161 i Matematik 2C.

Andragradsfunktionen kan skrivas y = ax2+bx+c på allmänn form:

Grafen går genom punkterna (-16, 0) och har vertex i (0,-14).

1. Vilket är det andra nollstället?
2. Rita grafen.
3. Bestäm b.
4. Bestäm c.
5. Bestäm a.
6. Skriv ett uttryck för funktionen.

Exempel 2

Exempel 2 (s 162) i boken handlar om att titta på nollställena för en funktion för att hitta vertex mitt emellan nollställena och sätta in x-värdet och räkna ut y-värdet (högsta punkten i detta fall).

Parabelns egenskaper i GeoGebra 2

I Malins övning skriv kurvan på annan form (x-k)², osv. Nyttigt men vi hinner inte göra den på lektionstid. Gör den gärna hemma!

Digitala rutan samt detta avsnitt sid 160-164 ersätts av en Övning i Geogebra på Vertex och faktorform av Malin C.

Överkurs: Andra kägelsnitt Av Malin C. Pröva själv att konsttruera med hjälp av mittpunktsnormaler.

Överbliven provupgift (svår)

Parabolic trajectory

Bilden visar en kastparabel.

Tänk dig att kastbanans högsta punkt är 35 m.

Längden på kastet är 110 m.

Utgå från formen för andragradsfunktionen [math]\displaystyle{ y(x) = a\cdot x^2 + b \cdot x + c }[/math]

Gör en matematisk modell av kastbanan.

Tips: Parabelns bana