Begreppet gränsvärde
Teori
betrakta funktionen
- [math]\displaystyle{ f(x) = \frac{1}{x^2} }[/math]
Vad blir gränsvärdet när vi väljer stora värden på x? Eller med andra ord: vad blir gränsvärdet för funktionen f då x går mot oändligheten?
Härhjälper det att ställa upp en värdetabell:
| x | f(x) |
|---|---|
| 10 | 0,01 |
| 100 | 0,0001 |
| 1000 | 0,000001 |
Vi ser här att ju större värden på variabeln vi väljer, desto närmare 0 blir funktionsvärdet.
I det här fallet kan vi skriva upp gränsvärdet på det här sättet:
- [math]\displaystyle{ \lim_{x \to ∞} f(x) = 0 }[/math]
Det här utläser vi som "limes av f(x) när x går mot oändligheten är 0".
| Definition |
|---|
Gränsväde i en punkt
|
Beräkning av gränsvärden
| Exempel |
|---|
| Beräkna gränsvärdet algebraiskt
Vad är gränsvärdet för [math]\displaystyle{ \frac{x^2 - 4}{x - 2} }[/math] om [math]\displaystyle{ x }[/math] går mot 2 ?
|
Numerisk beräkning av gränsvärden
Många gånger kan det löna sig att använda ett kalkylprogram om man vill se hur ett uttryck närmar sig gränsvärdet. Här syns ett exempel i Numbers:
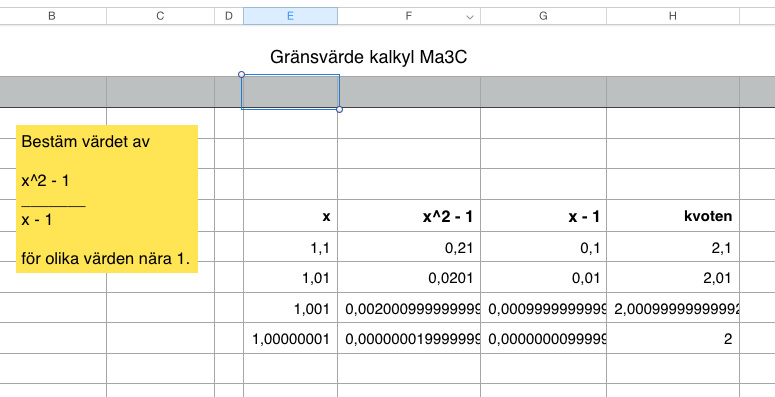
Aktiviteter
Uppgifter
Beräkna
- [math]\displaystyle{ \lim_{h \to 0} 2h + 3 }[/math]
- [math]\displaystyle{ \lim_{h \to 0} \frac{h^2 + h}{h} }[/math]
- [math]\displaystyle{ \lim_{x \to 3} \frac{x^2 -9}{x-3} }[/math]
- [math]\displaystyle{ \lim_{h \to \infty} 4 + \frac{5}{h} }[/math]
- [math]\displaystyle{ \lim_{h \to 0} \frac{h^3-3h^2x+4hx}{h} }[/math]
- [math]\displaystyle{ \lim_{x \to 0} \frac{9}{2+10^x} }[/math]
- [math]\displaystyle{ \lim_{x \to \infty} 99+0.99^x }[/math]
- [math]\displaystyle{ \lim_{x \to \infty} \frac{x-4x^2}{3x^2+x} }[/math]
Lär mer
|
|
|
|
Fördjupning
Rita grafen för funktionen [math]\displaystyle{ f(x) = (1 + \frac{1}{x})^x }[/math] och uppskatta gränsvärdet för [math]\displaystyle{ \lim_{x \to \infty} f(x) }[/math]

