Parabeln
Teori
| Definition |
|---|
|
Här visas andragradsfunktionen på formen
En pHET
- [math]\displaystyle{ y = ax^2 + bx +c }[/math]
I denna interaktiva bild från Wolfrm Alpha visas andragradsfunktione på formen
- [math]\displaystyle{ y = a ( x - b)^2 +c }[/math]
i båda fallen förändrar du utseendet på grafen men det beter sig på olika sätt. Fundera på varför.
mer om parabelns ekvation
Definitioner
Brännpunkt kallas också fokus Styrlinje är en linje som används för att konstruera parabeln
GeoGebra som visar samma avstånd
En punkt på andragradsfunktionens graf har samma avstånd till styrlinjen som till fokuspunkten. Testa genom att flytta punkten så får du se. Du kan även flytta fokuspunkten och styrlinjen.
|
18 Maj 2013, Skapat med GeoGebra |
Länk till filen på Geogebratube: http://www.geogebratube.org/material/show/id/39100
Parabelns egenskaper i GeoGebra 1
Du kan lära dig litet om hur parabeln fungerar och vad den har för egenskaper med denna övning:
Datorövning: Malin C GGB-övning
GeoGebra: andragradsfunktion med styrlinje och fokus
Övning - hitta funktionen om du vet fokus och styrlinje
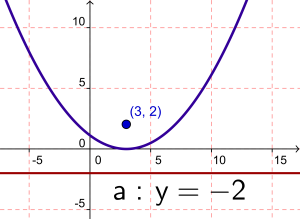
Detta är en viktig uppgift. Se även Exemplet på sid 152 i Matematik 2C.
Den här uppgiften utgår ifrån att du vet styrlinjen och fokuspunkten men ska ta fram funktionen. Se figuren till höger.
- Börja med att markera en punkt (x,y) på grafen i första kvadranten.
- Skriv ett uttryck för avståndet från (x, y) till linjen.
- Skriv ett uttryck för avståndet från (x, y) fokus.
- Det gäller för en parabel att avståndet från (x, y) till fokus är samma som avståndet från (x, y) till linjen. Visa detta genom att sätta de två uttrycken lika.
- Lös ut y ur ekvationen ovan. Det gör du genom att kvadrera båda sidorna så att roten går bort. Du behöver utveckla kvadraterna med hjälp av kvadreringsregeln.
Nu är du klar. Ekvationen du fick beskriver parabeln.
Aktivitet
| Uppgift |
|---|
| Hur gjorde man förr?
Konstruera parablar med hjälp av snöre, penna, fokalpunkt och styrlinje.
|
Lär mer
|
|
|
|
|
|

