Proportionalitet

Teori utifrån en diagnos

Titta på denna länk

• Uträkning till sista uppgiften på Diagnos 9 i Wolfram Alpha.

Sen har jag gjoret en busenkel GeoGebra om räta linjens ekvation (linjära funktioner). Den är gjord i tre steg. titta i konstruktionsprotokollet. Visa/ konstruktionsprotokoll.

Denna GGB finns på GeoGebraTube och heter Busenkel linjär funktion

Övningar

Här är en som är enkel:

http://geogebratube.org/student/m23347

Här är en bra men den ser inte snygg ut i Mac-Kan fixas till.

http://geogebratube.org/student/m23346

De bör bäddas in i sidan.

Direkt proportionalitet, 209-212

Teori

400

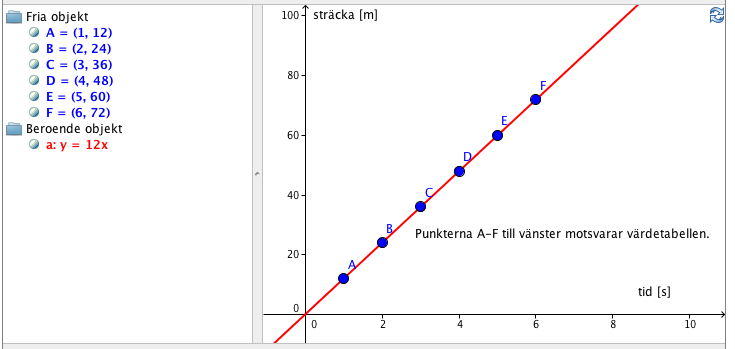
Direkt proportionalitet är å ena sida enklare än räta linjen. Det är ett specialfall när m = 0. Det betyder att linjen går genom origo.

Å andra sidan dyker proportionaliteten upp i en mängd sammanhang i exempelvis fysiken. Här kommer ett sträcka-tid-diagram (st-diagram). Det är teoriavsnittet i boken sid 209.

Exempel 1

Kommer snart

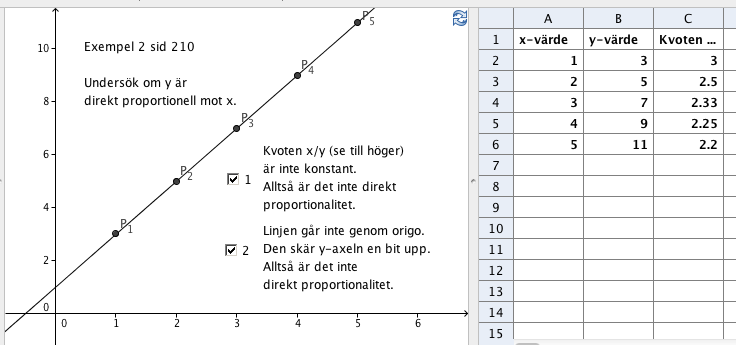
Exempel 2, sid 210

Den interaktiva GeoGebrafilen finns här: Ma1C Ex 2 s 210

Fler proportionaliteter, 213-215

måndag

Genomgång av Veckodiagnosen

Vi går igenom uppgift 3 och 5 från Diagnos 9. Trean kommer nedan men femman var enbart på tavlan.

Uppgift 3 löd så här:

3. Ulla lånar 180 000 för att köpa en bil. Lånet är med rak amortering på sex år och räntan är 5,6 %. Hur mycket måste Ulla betala varje månad?

Detta kan bli en mycket jobbig uppgift om man ska ge ett svar för varje månad. Det är ju 72 månader på sex år. Här får man själv göra några avgränsningar av uppgiften så att den blir rimlig.

Till att börja med kan man ju visa att man förstår att rak amortering innebär att beloppet delas upp i lika stora delar per månad.

180 000 / 6 = 30 000 kr per år
30 000 /12 = 2 500 per månad i amortering

Till detta kommer en ränta på det kvarvarande beloppet. Räntan kommer därför att sjunka månad för månad.

Här kan det räcka med att visa vad räntan blir för två eller tre månade, exempelvis efter en månad, 12 månader och 24 månader.

Excel

Om man vill kan man göra en kalkyl i Excel över lånekostnaden månad för månad.

Algebraisk lösning av uppgift 3

180 000 kr ==> Amortering 2500 per månad
ränta 5.6 % ==> förändringsfaktorn 1.056

månad     lån [tKr]        räntekostnad          att betala
 1        180              180*1.056             2500+180*1.056
 2        177.5            177.5*1.056           2500+177.5*1.056 
 3        175              175*1.056             2500+175*1.056 
 ..
 n        180-2500(n-1)    180-2500(n-1)*1.056   2500+(180-2500(n-1))*1.056

Månadskostnaden för månad nummer n är alltså 2500+(180-2500(n-1))*1.056

Intro - Fritt fall

Önskebrunnen på Tom Tits