Matematik 1c
Matte på öppet hus
Ämnesövergripande samarbete matematik engelska
exempel på film på Khan där man kan välja och editera undertexter.
Allmänt
- Miniräknare? Instruktionen till Nationella provet säger att digitala hjälpmedel (dator) är tillåtet på provet.
- Ma 1c.Kursplan'
- Matte A kursen finns på Wikibooks.
Grovplanering
TEINF11 Matematik 1c, period 1, 2 (4 lekt/vecka)
Vi använder Libers matematikbok Matematik M1c, av Sjunnesson, Holmström, Smedhamre. Innehållsrubrikerna nedan är kapitel i boken.
Vecka Innehåll 34-36 Taluppfattning och aritmetik 37-40 Agebra och ekvationer 41-42 Geometri 43 MD+ Geometri 44 Höstlov 45-47 Samband och förändring 48-50 Sannolikhet och statistik 51-1 Jullov
Extramatte
Mål
Repetera det som hänt under veckan så att du hänger med.
Hur
Lösa alla svarta uppgifter. Prata om de svårigheter som kan ha varit.
Mål
Repetera grunder
Hur
Testerna i boken
- Jobba metodiskt med ett avsnitt i taget.
- Interaktiva uppgifter finns på denna sida.
Miniräknare
Vi behöver inte skaffa räknare. Allt man kan göra på räknaren gör man lika bra eller bättre på datorn och datorn har vi alltid på lektionerna.
Tidigare var miniräknaren nödvändig på nationella provet men från och med i år är det tillåtet att använda datorn på nationella provet.
Vi behöver göra vissa begränsningar av datorns kommunikationsförmåga under provet:
- Nätverket stängs eller får nytt lösenord den aktuella dagen.
- Du stänger skype, msn, facebook.
- Du stänger ner nätverket och Bluetooth på din dator.
- Du ser till att inte öppna anteckningar eller sådant som kan uppfattas som fusklappar.
- Du sitter med skärmen fullt synlig och provvakten sitter bakom eleverna så det blir fullt synligt vad som görs på datorn.
Om vi gör på detta sätt har vi begränsat möjligheterna till otillåten datoranvändning på de sätt vi kan. Om vi trots detta misstänker fusk kan vi analysera datortrafiken på skolans nät.
Miniräknare i datorn:
- kalkylatorn i Windows, start - program - tillbehör
- WolframAlpha.org
- GeoGebra
- Excel
- Google Docs - kalkylark
- http://www.widgetbox.com/ som du ser ovan
Kapitel 1 - Taluppfattning och Aritmetik
Kapitel 2 - Algebra
Kapitel 3 - Geometri
14 delavsnitt på två veckor?? Vi behöver mer tid.
Prov efter kapitlet?
Nåväl, vi siktar på att göra kapitel 3.1-3.2 under vecka 41 och 3.3-3.4 under vecka 42.
lektion 20 - Geometriska satser och bevis
Första delen av Kapitel 2.1: Första lektionen gjorde vi sidorna 112-117 och arbetade till och med uppgift 3122.
Vi kommer att behöva mer tid för satser och befivis och även för definitioner och begrepp, ex likformig, biskektris mm.,
Definition:
En rak vinkel är 180o
Definition:
Två linjer är parallella om de likbenägna vinklarna är lika stora. Alternatvinklar Sidovinklar
Satser:
Vertiklavinklar Likbelägna vinklar Alternatvinklar Sidovinklar
Övning: Titta på alla filmer om vinklar på Geogebra
Sats:
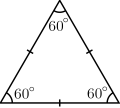
Vinkelsumman i en triangel är 180o
Begrepp:
Likbent triangel Liksidig triangel Bisektris
Lektion 21 - Geometriska figurer
Kvadrat Romb Parallelltrapets Triangel Cirkel Cirkelsektor Prisma Cylinder Pyramid Kon Klot
Cirkelns area
Triangelns area
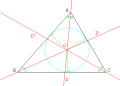
Triangelns tyngdpunkt ligger i skärningspunkten för bisektriserna. Testa på geogebra.
Arean för en triangel är basen * höjden / 2. Det gäller även om höjden faller utanför basen. Se exempel i geoGebra nedan:
<ggb_applet width="858" height="500" version="3.2" ggbBase64="UEsDBBQACAgIAKNicD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vrbcts2EH1OvgLDh04vkcSLqNhTMRk5cRzPuHVm5OahLx2QhCjEFKmQoCPlf/oL/YH8WBcXUryIsi5xbTfRC0kABHbP7h7sQhy+XMxCdEOSlMaRoxldXUMk8mKfRoGjZWzSOdJevng6DEgcEDfBaBInM8wczeqaGm/P6IunT4bpNP6EcCiGvKfkk6OxJCMaSucJwX46JYSVm3G2oCHFyfLS/UA8ljraBIcp75BTnEfzjOWDvZl/QVOWj+mJ9eYhZa/pDfVJgsLYc7Qj/Ujjd+9JwqiHQ0fr67poMR3NtPVKJzRZvHcaJ/RzHDE+XCwmJg+xS0LQf8yWIUHohvdasmsCgxFK6WcCWJm8bdgTEAxJ5oXUpzjiegoRYRBCn6jPpo5m2wasRmgwBT1sQ5ezeXGc+ONlysgMLf4kSQySGjY3wVI+WfIpBZFhQVsXXeUnMQ25GRPGQOAU4QVZgRkk1K88nKcncbhqmsc0Yq/wnGWJsLalmoTejgZrJVzgURSERLWBFt6UeNduvBhLECw59dVyLl4RArnBqziME5Rw5G0YoK6uvIoxXNJilC7G6GKEmoNPWvQbx6YYIa6uvEpT0UiKpjQ3cq1ziPGCpog3cBjBSQvlhZEdTUNZRNlF/gDecb1Slb/wezZzITrK/lHMaXytOYe9mvsMa4HTcKi+3fCnYa/x0vCaJBEJpa9F4CJZnKXSoUvB5BOPzuBRdihkMbf6H6CHbPVJkJBcfxmkEnfRW/HnWvOwlwvBZUhBZY8B1wAsjEPCyYBBHDra2y9/X+MInV68Ph1fnZ9pyMeMD+DBFZIZgchjwsuibEYS6hV4jzgTPRnCkpla2MpDQ/BSLEimbqUSADCgxRWBkOZTDHddI+eGJTBOWWkx3W+xr5Y2cvgAUqEnRPdcTgBsSIivSJapgEFzmFKEX0mggh/lnCU3kUDcDolVh8T81iE5aULyHZNG5BjfMTEabPKdThqYGN8AJAvYTlOeF+cKvfsLloBmR/txZDxDJ8ZP+Soib9JQr4Gk6ihN0ABNZrlqxCrLKEM26AvM+MWVlwI1fUvU9I16q707RQsF3lK5PfpcsrXMDnkassqJb0PMLBAzATFzd8TMh4+YpRAT5HkwYlaBmAWIWbsjZj18xEyFmLk7YhuJ6m2cpJDokjC8iufzOml19O7zNay1BTi8fAvk5TDWSkNRss4oFNsdUdzNMOAh7rCbxmHGyNiDVDu6iD1Bb7l8KvE3dFEFcq8b5H53NOA3E7ogq+KupbQt6iU2hbIkAt+DxVdceTCzbm8qUYtf47WGWr/hbmEnw7ZKuws315aGupxMUsKEawpIO8bxtmbUD7KiObAL9jA3m7G0fd2jHatsc7oX15RTAHEysDfVHJQErPhIVzbQD6OjKjZv/h/YWHtj09jczvKtrcrTz1CZDHbd8M7uF+YVUGJ7EZnTrkh58WyGIx9FeAbqvYvDZRBHQi3KT0IR1nmkIWxwp0LY5EpLjTKW918lFEcBCeWwQA7jR6oW2FUuqJZZg6dcMEesmKqVaswa1bSj31IE5ER9wI6qb47FlAT8qRAkuB9t9vamnJJyZ1pNtY0K5GMkx6Ty5JHO5iH1KCvcJuQRfw4hmKREHMg1zwWvCZnzc93L6CrBUcpP/rctIOvgk0cGficnPbh5LuA/fszwTx4Z/KstR4LfeeDOX+XvC5CxjbzrrO1uZmaubmEA9w6t2HYo8wDpqx34y4RNY9jIcLjGBGfSBG7DBN4OJvAekwk69cytAwXGceU3uHObFFFWM4crzeE1zDG6LVcp536jez7qKIE96JpVbCvQH++XCr6mKcOR1+LLowZ4b7/888En0WYIG4cm6qW2Inzrw9ud9WilxROc7qqFfGV7HdR+1TwjaNdilBC8Y1aO4ZWzs5PdVMlfqinT79oHGKRZjU1VNSaQQz8j5Qeoh8RBRLPuqss5vWsJOeBvYOflVc1hopZmumOZr8iC5X8T/PAxi9mvubAOks/ol1z+dZIzeF+rTnaf2wnEbcLecdJCak85PtJLP8sWPGerTE2VvLdDZFYgknYtASSjeRt4bvt/4H7h6fcVPIa5Gz5WBR/uvhV8ypGxBUi3/SWwBUgVotwRJfHZVAoBOSkONuU3VPyrnPzTmF3cDYJ2UG7W7TZ0qww+VoVRlcRHksTXsPdm3q6XWbg9OyzOZg17z/TQ1GXWIq5fv841uoahm6alm/2BaRv2wD7tGIM90saGpv95NdYrf2ckvtBTHy+++BdQSwcI2n+ii54GAADuKAAAUEsBAhQAFAAICAgAo2JwP9p/ooueBgAA7igAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADYBgAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />
All bilder i galleriet nedan är CC Från WikiMedia Commons.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Fraktal figur
Bevis: Vinkelsumman i en triangel är 180o
- GeoGebras hemsida har ett bevis att vinkelsumman är 180o
- testa vinkelsumman i praktiken
Bevis:
Gör bevisen på sidan 116.
Läs mer:
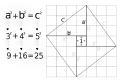
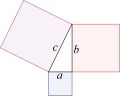
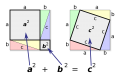
Lektion 22 - Pythagoras sats
Bevis:
Webbmatte om Pythagoras sats Fendt nr 2
Även här kommer bilderna från commons.wikimedia.org
Uppgift: Titta själv igenom Geoegebras film om pythagoras sats.
Uppgift: Hitta ditt eget favoritbevis på nätet och visa för oss andra. Bra övning: Upptäck Pythagoras i GeoGebra.
Lektion 23 - Likformighet
Lektion 24 - Trigonometri
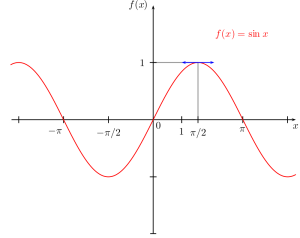
Läs mer om sinus på Wikipedia.
Engelska Wikipedia är ännu bättre på sinus.
http://www.walter-fendt.de/m14e/sincostan_e.htm Walter Fendt om trigonometri
Detta svar får du om du skriver in sine på Wolfram Alpha
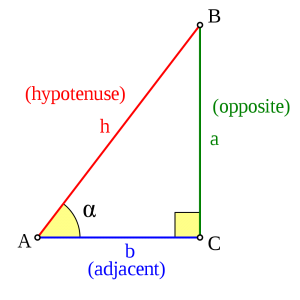
Definitioner:
- Motstående katet
- Närliggande katet
- Sin v = motstående katet / hypotenusan
- Cos v = närliggande katet / hypotenusan
- Tangens v = motstående katet / närliggande katet
Digitalt
- Grader och radianer
- Miniräknare eller dator
- Datorns räknare
- Excel - så här kan det se ut
Definition: Ta reda på vinkeln
Om y = roten ur x så är 'y2 = x. Dessa två hänger ihop och den ena kan ses som den omvända av den andre. Detta kallas inversen, den inversa funktionen.
På samma sätt som det finns en invers funktion till kvadraten på ett tal, nämligen roten ur så finns det en invers funktion till sinus och cosinus.
Om sin v = a/h då är v = arcsin(a/h) eller sin-1(a/h) Om cos v = b/h då är v = arccos(b/h) eller cos-1(b/h) 0ch på samma sätt för tangens
Lektion 25 - Vektorer
vad är vektorer och vad ska man ha dem till?
http://sv.wikipedia.org/wiki/Vektorgrafik
Vad är det för likhet mellan rebubbled och bilspelet xx?
Hur räknar man på kulans väg i CS?
Fysikerna ritar pilar för kraft och hastighet men inte för area eller temperatur.
Titta på Physics.fla
Den vetgirige tar en titt på engelska och svenska wikipedia om Bezierkurvor vilka används frekvent inom datorgrafiken.
Kolla vektorerna på fysiksidan.
Vad är en vektor?
Sid 144-147.
Definition: vektor
GeoGebra: "Basic Vector Addition and Subtraction for Dummies"
Definition: motsatta vektorer
Sats: Parallella vektorer
Definition: storleken av en vektor
Mån 10.05-10.55
Addition av vektorer
Sid 148-150.
Sats: Kommutativa lagen för vektorer
<ggb_applet width="960" height="490" version="3.2" ggbBase64="UEsDBBQACAgIAGRkcD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VndcuI2FL7uPoVGndmbTsA/2JBZvDsEMl2m6aazSXPRO9kWoGIsrywTyPN0X6EvkBfrkWSDgZCGlE3T5sZYOj7S96Mj2el+WMwSNKciZzwNsN2wMKJpxGOWjgNcyNFJB394/6Y7pnxMQ0HQiIsZkQF2Gw5W7QV7/+a7bj7ht4gkOuSG0dsAS1FQjPJMUBLnE0plvZkUC5YwIpaX4e80knmARyTJVYdJMUyzQlbB0Sy+YHl129TDZQmTAzZnMRUo4VGAT51TrH7dUCFZRJIAtyxLtzgBdjxroxOaXNU74YLd8VSq8HXyhIQ0AfhXcplQhOaq1zVdIwhGKGd3FKhyVFu3qRno0iJKWMxIqmDqKUIQQrcslpMA+20HRqNsPFHMdVomW8S5iK+WuaQztPiNCg59jtNo2x3f99teu+16tofRsuyyO412y3d8y7Ns17UBbw5YYCau1+h4HcfyWxY86Dsw1nJvlx6Zzq+olIAxR2RB84rpsWBx/fcwP+NJvBIn4yyVfZLJQmh3uGWTJirAQKhQCHvpOKFlmw3yTWg0DfniyrDmmtTXy0w/oqcTjvs84QIJJRUgHpfX0Fx1jJrnKsrSMZaOKHOopKt++9TREfoamqvRlqVmaiVuuwJtW9UwLEeqAZIrU1d0aFMEGKMiZfKiugE3TddIVfynYhbCYqr7aZXSPlLKbnPLbd2tZbbjP8ffsV+3ufNQd0pFShNjzRTsUfAiN/43DtBwYhqxGdyajpJXojT/FXCY1piOBa3gmyVtWNe9Vt3+W83dZjUJNYccIEcSKhPQIhUlJI6ZvidzKFpTyQUUgBmapiTLVFmRsKQD/PH+65Sk6PxicH51PfwRo5hIeBirUW+5mGrM13QhEQn5HHp6g8Hwenj5CfVu0M35T9eXn88/g3FootSKIqRnFvHZjKQxSskMHhmmEkSB4qWzMlWwELECvOiB3DAVO8BL/VNj5YWsAnoGZplNlY6EzijUFamXhF5RK3P08Kq6cl0qt8yzdhl0r+zvt7T71SU0F5JkEwIUN6yqxi2BuLoaOuHPPH5AoxwtzKNoGeAT/ePObBU6xtQAZbd1qQSLGlR/g+/sWfjqy18XiufCIylYWfsJinCmEqg1l1Eal1uhLMsUyiClLnq1lbAmxy7J8Q7lZtNTN0AAF1uG6hkzne0YqXjcSHOTrGKywJv1T06g0KQ0h7pyusbZfFyODfBpuRRV+GUZPdoVy7FaG9X6CF7cpnud6inwanUnN4U2IkLSHMppiV/C/S9KOUQX2WrFPs3R/f+Ho72SYufbObq/4+j5QY6ev4ij94ple66Wy7OPYeltvl/a0puyXcCgW6L1jWjFjmjkcdHU/Fdsk/2SOc+RbN8SOkqVOak0sUtNHPdRUbYR0C/phiRsBm8tEZMHU39mqJ/vUB8eQH34n6Le2arwJy/C/b4zHTEChDsCDA45yw1ezVnOdjuVtf1dcx+vwg92CLs9qMLfHrnC791xraPQ6pektl9FDX9QmP4+Ye4OEubuCcLY3rfYe/Wu+ypOkxW+g3XrP0O3s326RQfpFr2Mbg+8BWyemY6i2zOPTM/W7WznNWCRCcit0JfMqG8KcBzU4W+/FFy+G9AUhcn91/JrRYru/xAoL5Ra6hvG2+9t610MMeL+z5ggHk2QuhvDbUoaJoUedlNWCePgzUH/zY27xpTevVsNy7Hqf54Wym+0N5qd+pvF/verkPOEgigVFnM8gvGLcha178L/4LXr6fgvR6OcSl3xfbOLuvajliWZXiK6TQmNfjAKH4Z79Ipwe+XpwX8ybg0YgCv827ib9U99+pt6+d+G938BUEsHCCGqX7tbBQAAnxgAAFBLAQIUABQACAgIAGRkcD8hql+7WwUAAJ8YAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAlQUAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />
Subtraktion av vektorer
Sid 151-154.
Definition: Subtraktion av vektorer
<ggb_applet width="679" height="385" version="4.0" ggbBase64="UEsDBBQACAgIAGlUgT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAGlUgT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VjrjtM4FP4NT3GUnyydxo5zKWpBMCwCCVikYdFq/7mJpzVN4yh22g7icZYn4cX22E56GxaYy7KLRLEdn5zj8/n7jp0ZP9osS1iJRktVTQJyEgYgqlwVsppNgtacD7Lg0cO745lQMzFtOJyrZsnNJGDWUhaToBDTOKNRPiDZeTZgGcsGU8GTQRrRLBnllFMyCgA2Wj6o1Gu+FLrmuTjL52LJX6qcGxd4bkz9YDhcr9cnfagT1cyGs9n0ZKOLAHCZlZ4EXecBujt4aR05cxqGZPjHq5fe/UBW2vAqFwHYFFr58O6d8VpWhVrDWhZmPgmSLA1gLuRsjjnFFHMaWqMaAalFbuRKaHx1b+hyNss6cGa8svN3fA/KbToBFHIlC9FMgvAkChmlhMYkI6M4jEkAqpGiMp0t6WIOe2/jlRRr79b2XEQWgFGqnHLrET5+BBrSEO7bhviGYpMkfir0z8LIN9Q3zDext2H+deZNmbdh3oZFAaykltNSTIJzXmpEUFbnDe7edqzNRSnceroHu+zJfcxJyw9oTEKE1EPuBvftL8EfCzus95Ike1FN014xaB+SJfH3h6Q3CRn1IWk4uhySxv+QZfIVcP0avidNEu8hi6HcP/e7FDGiV4jox98KGGU2YJqxLwZM2A9JcTzslTLuxAF6bm27nTRiqa1cohHEI8t6AjFKI0mR5DGQETYpBRQDkBhYjEOSQWLbFKIUJxhEkIG1IxE4bcQZ/sdS5yyBGJ3ZpylKEggGYhBHQJykGKCQwMkSJUojtIhjiPElG55Q6yJKgCU4ijJguEaryJSgYYQv4hjDU4gIRPZlkgJNILH+CLNKTzK7dHRJIQkhIdYhihoF7cWM9hlENpukg0tWdWsOIMqXRd81qt7uBVpjOdoVPV+eDmrinXHJp6LEY+LM7iTAipdWES7QuaoM9JtI/bNZw+u5zPWZMAbf0vCer/hLbsTmGVrrPrazzVWl3zTKnKqyXVYaIFdluF2zKslen25XjYNob4LtT8R7E8leP/1iXIUz0GqB8VWje3NeFC+sxa40IJK/VeXFk0bwRa3kYRrjoTtxxqLNS1lIXr1DstooFhfoDyBXrfoDKErSfiGqKc4uNDIYNn+KRlkcwxNK0yRhyYhELMqw5Fz4KcqSE5oSmsVpSEYkRPXpnFvtUXKSjhhlYToKRzSKMdbF/lSKEeMsTAkZdZHFartBfCO2uc8aWez3X+gnqiy2SLjkT3lt2sZdHLAyNjalx9WsFI4gTtZ4KueLqdqceWZE3tfbixpHoY8/nTnQobFVFRNBZ9Que+rHzsYubGsVOpvQWYQ91WSxnScj6ixcO/Wts0Lu+qV1iZI+SxL2YaR25SwMDkTjiG/P+LaS5mU/MDJf7DK19q/b5VRs6XPoktySy/HwiF7jhWgqUXZsxo1sVau9OPeIXohcLnHoJzpAuN2s33EB/mkhZo3o1126K5mHy82G+0S99Ni5etao5Ytq9RaZcLSA8bBf5Vjnjawt32CKJ8BC7DhVSM3xACn237Pyw9Rze1AgPMZC87gopBurfA66nZqGL9yYr/BiuzCqEQ2KtzVzhXR4/vnTglfwa4mXM23kDONgDUK0rVJLscR7GRhHSMfp7dY8dhc+uwegpu+xDB5t3W6PcfqL5HQ05mU95/ZS2AFV8gvRHEDn/L1SxTGguF8uK6wJtedDLYRnkl8vdmp05/R3UNNwhzRsJkFmr+wX3dX9g7/s+9uuzdRq8qCI+6dHW4t88yB9A64nPz9chHZ4ZbeEV66WS14VULlr0DsERTXB7lzmoWUZcGLR89C0pp9ovbPOxSXwV95Zj257Y/TD62O/Q5AdEW7nalt6DV4JFvjZo91V3HQnges8l0Uh3HXwuNJoXxNz3hihsfJ5A/zUa8wbuwkgNrXF8gp8Pf35+Zr8QHk//fnhYj9e3ade3U8vqXt1JXWv/h/qHtD/VN6nl/i6qRuMZFnRAbEOvGkLv8AqOAJz+C2Y19eC2fH6doE+Poe+jjO7Ec5fB/TzXx2iFO5BCwP8PL53DWTRzU0ZTOLoNqAlfRUYfB+J/1VwP23pOrgOqJ+uBar9c+Ssw/O2CNufROEPxnS4/3ngPsC7PyU//BtQSwcI8oYesjIGAADnFgAAUEsBAhQAFAAICAgAaVSBP9Y3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICABpVIE/8oYesjIGAADnFgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMkGAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Ovanstående GGB är skapad av Håkan Elderstig fria att använda enligt Creative Commons. Den finns att laddas ner från GeoGebratube.
Vektorer i koordinatsystem
Sid 155-158.
Definition: Basvektorer
Sats: Räkneregler för vektorer
Sats: Storleken av en vektor
Fredag: Diagnos på hela kapitel 3
3.4 Vektorer och trigonometri
Sid 159-163.
GeoGebra
Länken går till min sida med GeoGebra-grejor.
Jag vill att ni ska ladda ner programmet och börja lära er det. Vi kommer att lära oss tillsammans för jag är själv ingen fena på det.
Här finns en GeoGebrafil med addition av vektorer. Lek med den och försök göra något med vektorer och trigonometri.
Kunskapskontroll kapitel 3
Tyvärr var inte resultaten på Diagnos 6 och 7 tillräckligt bra för att vi ska kunna känna oss helt klara. Ni kommer därför att få en uppgift som ni ska göra individuellt och lämna in. Ni får göra den hemma eller i skolan på er lediga tid. Det är lämpligt att ni samarbetar. Uppgiften är att du ska lämna in snygga fullständiga lösningar på diagnos 6 och 7. Detta ska vara klart senast fredagen den 11 november.
Ni kan få papper på måndag men Diagnos sex finns här och Diagnos 7 finns här om du vill börja med en gång.
Detta är en kombination av hemtenta och samarbetsövning.
Uppgiften: Du ska göra om diagnos 6 och 7. Du kan jobba hemma eller på rasterna i skolan. Du ska jobba själv men ni får gärna samarbeta. Det är inget problem om det kommer in liknade lösningar men jag accepterar inga exakta kopior.
Krav för godkänt: Minst åtta poäng på varje diagnos. Extraberöm för snygga lösningar.
Mål:
- Ni ska kunna geometrin
- Ni ska öva er på att samarbeta och repetera med hjälp av boken.
- Ni ska upptäcka fördelarna med att plugga tillsammans
Snygga lösningar:
- Skriv alla dina lösningar på rutade papper i A4-format.
- Skriv ditt namn på varje blad. Skriv lösningens nummer.
- Använd luftiga marginaler.
- Ha luft mellan uppgifterna.
- Skriv av det viktiga från uppgiften.
- Använd figurer.
- Förklara vilka satser och formler du använder
- Redovisa dina beräkningar
- Stryk under svaret eller skriv "Svar:"
Kapitel 4 - Samband och förändring
Kapitel 5 - Sannolikhet och statistik
Kapitel 5 handlar om Sannolikhet och statistik och består av nio delar (en del har teori, exempel och uppgifter).
5.1 Hur stor är chansen?
Intro
Khan Academy om Probability
Här har jag börjat skriva undertexter (subtitles) på svenska. Det är enkelt, bara att skaffa ett konto på Universal Subtitles och sätta igång. Vi kommer att göra övningar på detta så småningom, där ni får en film var att översätta.
Sidorna 244-248
fre - hemdiagnos denna fredag.
Definition:
Sannolikheten för en händelse = antalet gynnsamma utfall / antal möjliga utfall
med P(A) menas sannolikheten för att händelse A ska inträffa. A kan bestå av flera händelser, exempel vis att slå över tre på en tärning.
P(A eller B) = P(A) + P(B)
5.2 Oberoende händelser
Sidorna 249-251
fre
exempel 1, sid 249
<ggb_applet width="629" height="465" version="4.0" ggbBase64="UEsDBBQACAgIANpWeT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADaVnk/AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1Z3Y7buBW+zj4FoYuiBTI2/ymldhaTtLMNmt0NMGlR9I6WaJs7suiVZI8n2NfpK/QF9sV6SEoeeZxJ4kyQDrYFMuHfIQ/Pd853SMqTb3erEm1N3VhXTRMywgkyVe4KWy2myaadn6XJt8+/mSyMW5hZrdHc1SvdThPuJW0BlRkzc0bmZ4yw/IxjWZylGKdnmRZsnhI9l5glCO0a+6xyP+iVadY6N5f50qz0a5frNihetu362Xh8fX096lWNXL0YLxaz0a4pEgTbrJpp0lWewXIHk65ZEKcYk/E/vn8dlz+zVdPqKjcJ8iZs7PNvnkyubVW4a3Rti3Y5TSRTCVoau1iCTRKDTWMvtAZA1iZv7dY0MHXQDDa3q3USxHTlx5/EGir35iSosFtbmHqa4BHFHKdEMioFw5JQgMPV1lRtJ0w6peN+ucnWmuu4rq9FmBPUOlfOtF8S/fILophi9NQXJBYUCinjEI59mMWCxoLHQkQZHqfzKMqjDI8yHPa4tY2dlWaazHXZAIS2mtfgvn27aW9KE/bTddyaT56CTY19B8LMYxoxh36Mn/o/APop78EeGEkGWtt6c6LSXiXP+KerpA9RyXqVhL3HSirusVJ+ANy4h08xk4iBTlAV/oW/I42MnqAxth+mUPKvYuJk3DNl0pEDNUsv23myNavG04VlSGQ+6gkSQA2pIMgFIhkUiiIgAyICcQFNkiLpS4WYggGOGEqRlyMMBW6IFP7jKiwmkYDFfK8CSiICijgSDJFAKY6ASCjQEihKGUgIgQRM8uoJ9UswibiEFksRhz16RioCggwmQhvUU8QIYn4yUYhKJP16hHumy9RvHZakSGIkiV8QSA2EjmQG+RQxb43s4LLVetMeQJSvir7auvXeFyAN6eg268X0dJAUn0xKPTMlnBOX3pMIbXXpGREUzV3Vot6JNPYtar1e2ry5NG0Lsxr0k97q17o1uwuQbnrdQTZ3VfOmdu1LV25WVYNQ7kq837MryaBO97uGBhsM8OGAGAzIQV29V6+DEbRpDOh3ddOL66J45SVuUwMg+WNV3ryojb5aO3toxmQcjpyJ2eSlLayu/g7B6rV4XFB/AoVs1Z9AnKt+I64uLm8aiGC0+6epnceRjFKcCqwkxwQrAifXTRyCo2XEeSozQjPCFPzB3nLtyZeJUcY54VJkLGVMpjBpMERZlkmCCUkzIqJqs917SO/M3vhFbYth/VXzwpXFHopg/Uu9bjd1uDrADmpv03m1KE2IkMBrOJfzq5nbXXZpM6719mYNLRz1zxYBdQSZgQoBAl05i2WQ8RvbS+Egg4ME7mPNFvtxktEgEcpZLIMUBG/cWmco6a0kuFdjm5DPcHLAmhD50+Ti13/XcMFAVxr81CZoU9n2dRwCOtn86tZuP/uHzWpm6sNA32sg79VwXhX1A9afjO/E3uTK1JUpu1AHJ2/cponMHWyqMLldQTMOdGBp78i/wQ5ib2EWtemNKMOFLUIZRvEwio+6w1IXtVu9qrZvIUrubGAy7nc5afLarn0sohkcD1fmNt4K22g4XYrhPM9NgC/3pwjg03psgLWbdukgDCA+DeScBcyFpAMjnpqlWcFFDLUhAEMM32IfrngeWORmP0Heu+Ob0Aj2wPC9IQuRo8v1UvuLYGd+qW9MfQBIWPF7V9yFCbwQbAH3r/0C3tFrY2K4xD1DZQ0LBs4dJDJAvkG77kp/05XvYhnvuN5az8ODzB1777gM4igC9RHIXnwWZIIExHzxGACjXxGwl58XY5gfpLxHEmH0KwD2p88CLJ4QRLAAmA+0xxFiXwyx3bo2jX/C9zi8NbsWtgED0+R3P29c+8e/lnprYjVMP0QZbmG3IMfJHwZ6YNcx0g8OTDhV6/aNNxvFCEulVFhIxSWByw6XAb4zeFtzISgWhCqRSgaP7CGeH4eIHkJUu0p/OkT0MUGERypllCrFlRBw0RtAxATOhMioxFJlcME8CSH2EITYY0IIoBASp4wAPFRxIigPEOFRJgAvwTBXmIosOzGG+ENoxh8ZQhIQoFRgkaU0zRTtTsJM8SyF0MpECmHE03sR+kDq/vOxqf3L/+O5G+/v///1w45kmKTw+sI8Y4SmssvkJGU8FSngQzLGv0haz91qpasCVeGzyUtb56VJbt/xGvsLBNLEYxtx27T9QB4X65Y4cg1clW2+Rz7/9CiEiYWNKPrHbyc9u/8iTDA9ClN2mudu32ntEl49FXBwmqjeZf7Tm6/9xRaFCV+P4jPWLky1hd3BAx6iG/f3FBxDB73re3YkRL4fI/2tjwycB0FT2x067+XPe6lz6j+DZwwTSZQiwBlKMuhmnYZzDgtHSQE12i9ofq6iNU18vvmPKnZu81PIdPGbIBP1ZFISeCQEZhj7j/Eh3xBFqUwlVWlGiM9CX4dNLyKbLo7YVJzCpuL/bHoAmxgQCtIowQrjIzbRPZvIl2TTd78JNt1zNEG3JClnCisF4DLxtdh0Htn03RGbzClsMg9lk/5fZRNc25iSTHDBORcY+x8e7zucHkinmXOl0dXeKTo4DXDamKOvi5/3eD/1rvvjfN6YNtCCZoEHnH7Ij7leh8gJfW9+f+UfOsii2a//KroPsNUf0BTBc0qcBsXsEUKh2AlQrG4qMN7/nKdr5Ep7pVFjC1dHOI7QGA+/woYfQbrf85//B1BLBwiq/ZEU1wcAAGwgAABQSwECFAAUAAgICADaVnk/RczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIANpWeT+q/ZEU1wcAAGwgAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAbwgAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Kolla gärna Mikael Bondestam som förklarar kast med två tärningar = sannolikhet vid oberoende händelser:
Här kommer en bild som är lämplig att projicera och sedan rita på om man diskuterar sannolikheter vid två tärningsslag:
<ggb_applet width="540" height="413" version="4.0" ggbBase64="UEsDBBQACAgIAE9OfD8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAE9OfD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Zttc9M4EIA/w6/Y8WeaWJbkJEwKA4VyhfJyV+Bu+HLj2Eoi6lge23lj+PG3kuzUKdwdHIzmRp2melvtah/tSpppO324W+WwEVUtVXEakEEYgChSlclicRqsm/nJOHj44O50IdRCzKoE5qpaJc1pwLSkzE4DnnAxo1ycjFlITxiPRycJmdOTbB6mk4jP2WQ8CgB2tbxfqFfJStRlkoqrdClWyaVKk8YYXjZNeX843G63g87UQFWL4WIxG+zqLABcZlGfBm3lPqo7mrSlRjwKQzL84+WlVX8ii7pJilQEoF1Yywd370y3ssjUFrYya5a4ejYOYCnkYtm0jaEWKhFIKdJGbkSNU3tN43OzKgMjlhR6/I6tQX5wJ4BMbmQmqtMgHJDxaMLjKGS0LQNQlRRF0wqT1uiwUzfdSLG1enXNmMRJjVL5LNEq4fNniMIohHu6ILaIsIhjOxTavpDaIrIFswW3MsxOZ1aUWRlmZRgNYCNrOcvFaTBP8hoRymJe4fYd2nWzz4VZT9tx4z65hz7V8hMK0xDjxDLH/jC8pz8xfpgeGB47SXpWm2r9nUY7k4xG324y+hGTtDNJQvqlyYj/jZfxP8C1a/gWNwnvkUVT5tt8vrBIo++waNs/ZjBmTlycDrtMmbbJAfVSy7Y72YhVrdOFToBPdNQT4Jga8QiDnAOZYDGKAJMBCAfGsUnGEOtyBHSEAwwojEHLEQomN/gYf7CRURYDR2W6d4QpCQQNMeAUiEkpBphIYNISUzSiKME5cJykzZNIq6AxsBhbdAwM16gzckRQkOJEbKP5CCgBqieTEUQxxFofYTrT47FeOqqMIA4hJlohJjUmtE1mlB8D1d7ELS5ZlOvmCFG6yrpqo8rDXqA0Hkc3p549no4OxTvTPJmJHO+JK72TAJsk1xlhDM1V0UC3iZHtW1RJuZRpfSWaBmfV8DHZJJdJI3bnKF13to1sqor6TaWaM5WvV0UNkKo8PKxZ5aRXjw6rxgbtDbD+AO8NxL366Kt2FY7AuhZoX1V1J55k2YWWuDkakOTrIt8/rkRyXSp57MZ0aK6cqVinucxkUrzHYNVWNBfobiBzWnU3EJ3wbiGqyq72NUYw7D6ISqEgGdBJ72uMOba3QzSOBnjSHL50AqWJzj3OBpOjSTinG+J4hRtjYnPYk2QnDu4uKpn16xf1Y5VnB+eNv2dJ2awr81jAE7DSXjwqFrkwMWEyGW/i9Hqmdlc2GKjV9XZfYqu1P1sYzoBnQcQ5CrTlzJZGRi/sIBUamdBIhF10yewwTiaRkTDlzJZGCsPVLq11lHRekrAzI2tzgoXBUZ6YWNf3+rqQzWXXaGR6feOpln+1Xs3EIWKOVZKfpHI6vBVR02tRFSJvAxg3cq3Wtc3HXmxnIpUrbNqBFkiiN+sdLsD2ZmJRiW7duXmGWVxmNOzH5hfdRtV5pVYXxeYtRsKtBUyH3SqndVrJUscbzPDQvxY3MZXJOsE7I+vP0xmHrqf6bkA8jUaDubhulgq3GmNQ4EmywLl4lOCITrhcrPB5BY0JMhOnB9yPzMNNcwU1+4in2a3tuNk3HP5qwJnQTPJymejHXet8nuxFdYTD6HupstuQcA+MJ5japd3jUggbHXa9WClRncmpo6MJqdewax/p+7b8ZEv7atWe6jw7Oott763twhiykP4F1+P/Fy58TP8HYJFDYGc+AKMOgT3xARhzCOypD8C4Q2DnPgCLHQJ75gOw7paMHAD7xQdgkUNgFz4Aow6BPfcBGHMI7IUPwLhDYJc+AIsdAnvpA7DulqQOgL3yAVjkENhrH4BRh8De+ACMOQT2qw/AuENgv/kALHYI7MoHYN0tyRwAe+sDsMghsHc+AKMOgb33ARhzCOx3H4Bxh8A++AAsdgjs0Z/EB2TdPcld/GbSD2SRQ2RnfiCjDpE98QMZc4jsqR/IuENk534gix0ie+YHsu7GjF38ltIPZJFDZBd+IKMOkT33AxlziOyFH8i4Q2SXfiCLfzKyYf+PZc1foLf/TPXgL1BLBwhhk6/x7AUAAOk1AABQSwECFAAUAAgICABPTnw/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAE9OfD9hk6/x7AUAAOk1AAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAgwYAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Khan Academy
Däremot får alla gå in en kort stund på KhanAcademy på slutet av lektionen. Alla ska välja mig som coach så jag kan se hur det går. När du gör övningarna kan du klicka på Add coach längst ned på sidan. Gör det och adda mig.
Mitt ID är hakan.elderstig@gmail.com
5.3 Händelser i flera steg
Sidorna 252-255
må
Khan om oberoende händelser i flera steg:
Sedan en kul grej bara.
Rulla tärning från http://www.geogebratube.org/student/m712:
<ggb_applet width="408" height="311" version="4.0" ggbBase64="UEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAANjJhZTM0ZjBmMjFhNDI0Zjg4OWQ5ZWFjM2VhN2VkZjdcYjEucG5nAa0EUvuJUE5HDQoaCgAAAA1JSERSAAAAWwAAAFsIAgAAAJNUbs4AAAR0SURBVHja7Z3rS1RBGMbPnxWCkliW2IU+SCBkEpqgRnZBI7tJKFhaCppZimiKdlExM8vYvBVK3ipFw2QTlc17UYpsEtsjs7yOZ9fdLWLXnXmH+bA7zoF9f+e9zeHwaDi8Dfv6767h2doOa179SGblYJBO/P7Wvpnln3av9hoe/tY7Ng8KMdnth7MsykzQARrc5r8jMvxlOb28XyUQphmf320ZsvlK5En3pOn6tNJ38LqBz4sg5Yvj7ZwBX8BvxoRROQ8/muzCiquzGKbrESbyNYVNo3Pf1hyqjJW1ddza2NxO+WZjcVsiMg7Em0osTFxKWj7JUGRPMdwGCy7wkHvUGE97puTwMRNBjpBxOPQYKDpkNQBtIQLPoWBR3jvkUfZynKqPMNwQfYdYResRXKXkvxQjsBDmV1kmnESyat6LJQBz6DfQkQvzUYM2iCDxUleqm4PQSCx8KwigczHQulEGceg6KJsgcAyqzJRsNRxwDQEBZxeDkghWtSWCdCEgIHyMlOIe8WV6YdWh8aDGxKCkolUb4iG5bhJx6D2YCBNhIkyEiTARJsJEmAgTYSJMhIkwESbCRJgIE2EiO53IwOhUZXPv5eLm5Jy6jILG+w1vsGL/ta4jkUnb0tH0sl3HbrjO6NTing9WvYjAL8JO3HKLg+b1e8/97yyBIQIcZHbI8fzw1IrIs3VRF5oizz2KOFUZEn+b/oo4Up/I+OQceUdo4p2DV16Y3pM7dLUtPKWcoDzrGlaZCKKAckfYyRIP71VGnH4gtu1NKlz8vqIskc7+cQoWV+/YMq+9Ck0oEpsRZcoSQXEVRiJfeH39FmnF/9nE30RgmzBy3/nHXolEX2wWm4+cKVWWCGwTRh641OLLW9qUX5UlkpBVLSyMymj0igOJhpKrskQKql8LI/ek1Xglsj+9XmxGg68sETQXzk4koQjVxDOR3cnOOg2OyhJBZ0HtGToODziQeimJ+POME4CetcEy5DQ1Lg/11S0OZBk0LGIbjsXqn2vSbm7e/7CkuzjRoHMXXRk+yy08DsH+bFgDRgRGUtHZnHF5phWUGP8/Ewjk8xHPDwTgR372jh3xDG3StoQ6guJKIOA7uRVtOP7o+1Rxpw0mwkSYCBNhIkyEiTARJsJEmAgTYSJMhIkwESbCRJgIE/lXIqQboKqylY9jUzcgs3KQtSVW1tZJzcgobBoVX7qGZ7UlMr2wStpoRm2HleTxtCVCWnCAYBCe2NxObQU3KHVYhmwbWleUXPUU7rF+/UFpFQllg0iVZcKkkqbVIE1OoSW4QWT5p53kKJFWtMIhyyfCWRykIijLLvaOzesTL+QKpCbpJIJgIdHemOx2HaAAB/Wp+EDqeIbcpdAO5bMsgoW8Ax9EvJiJiEZFhoJ2Rb1GFocVWd4YOEBH3mC49rMmzWtwQQMT7Kce2NXaN2OSesbtl73DPRGRU1BxthNFB6DgUoonsVHTzKsfcausua1ePHbLYsiKSca7uoZ3IuQvOAGi2yeR3yCdCBCEjC//VuAP04ihAg09G34AAAAASUVORK5CYIJQSwcIT3u8qbIEAACtBAAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAAMDhiMWI4NGQxYmExNjkyMGI2MDczZGU1OTMwOTMwNTNccjQucG5nlZR7NNMLAMd3vC5j7n4sr4ZrppSMlRAW5idEM6/OQaHMo2IXaW1aHY/lGUXm5jGvbqQ7jzVFrou5siUmdkuRYR73hpFHRkrX/eP+f+8f3+/3fM/5ns+f3ywiwQ0G1YNCIBCYhzvou5vB/0hZbtfv+pOFEIiilQfo7E8dlbK+eiKcdfiyRg3RML3e8zne0lk5ycg0FQqtutWVCRX1d4WgfdDmPa/UgP6T5k/cAU2sWb2XhLiWgZEUtHYcXrWSsrYTlt4LpQOWju+lA0IhvTyqnBY5RSOoFjMdO9N2eDvP3hTVPepbWT0SH4TduVm+NNl3VbR1UanTPE8trdspfmhtXLG8rlLeCs7Focx+3N/bR6CpMBrUpROy+uWsAFTF2FiirPMYDRnU4mAN9T2N8C6XO9t1zwdb98JT+8paNzMuYihRFl78UeY18ubL6rZLyIFfUiDgdnUzQ9saQ3Zn8FM+zZlo2WGOtMxTTdtrogFtVbJlE05sunbbbmv2/n65vbxpZZMTvBoXrlLlt0yny9Ecaoj95uoUGSc9HiPRW7N/G9BqsPKEaftYN0WxdCfmssguPyt7bVEj+aZGY5dxlIhv0HxCIf2n9mHQD37QOOP7w3Ifz1i1kknO7KsrEYnrAX7T05ejDJG4YR/K54iv+mcCYUrT4yVhU9HNR+5yjmJeVszpbWiFniJAG23W6NzfXRq8LtzVSL1oqWz7azQJjHu9TnB4si/2Eoj0v4bx7/ENRObD+xXTkmfv/3acwri+tXVFjPgOtxh0MsEvMimYTBlpYEntH5dyn4Z6n6oJNXrwdjKOiJ+5F03yvzUO/9Zvn7Qx0PyHONVhvK6u0bIRa8zqxW61minZIgvh8ZtuPX/9AFcriBQTxi7G9ZFfCMMGyDMkxaIiBXIxwVNgkC/7OuiBmBqcWxB1p7bFHmBjSabzD/c54TcyuxK5N6pyayzCK5ur67OUVd4Zpz7jEAyXBFiTYdZyeO6CDAFFofC7yzDyAsV+ImqWpV8f4gyC7rvYaxnqTQT7689qjJP1RMN7QJDBWARop/0GktorWBc+b6qHYi6pyXzgAKDx2E0hWHsBcRr6tI+qANO9wMba/sudqB4w3C7mTXOaPFyfs+L/IQOFKxlS9sS8uUeTGKiA6fdSBCVTr0yEOE0jozGQOOqNrBUviFp4oemhgg06fU4fRHIYdmwUGgEDvAq89ALU3K8qKh2yXlYoYxKtQDbSBntyaNTIHT+kea4RHfYgrO1DnU7gMvNlXEP4twbBAZXY7MyY54AKLTuTa1GxB3AFAR8Q8d8jn4FGBfcMzfE1ccA7VF6ZnnchSMqxTYhzGILnm0sEA5sld+iAG4Y/ItCKn7lBz40B3Jb+T0Fbd6SvKulEPS04KHHvoe7MwnQsHMOxLQx/wE2YF3UUXhlzYjQxFrYtMVy0eR1Qh8pDIgcHG9cK954qvRRbtU4tdUzmH5YIeCtEjK3TK+XBnGGNHFrnz9m2CSQHkl3HJ1zgyyuuva/PSwxuMw25hi/Y3ZVsoDiWPBzh4fkQf+xYIIZ3FMVjLhfmaUSaVMV9/KBZdcioDyWoPXsGqUso+4R/5PQOPZIVxiEOi1Mk1WCyHHKmViIfwRdRLW4GUcV95zl3KJPywRZJqH6fqaqus5wCtHkHVN2MnhQ+CdHvSNFaGpxPCElTRd6jDv6ZQzNfT1zwxbl8aaeA+7pjoJSy3IJqeSI9IruWdL/NLiBAF8udS9+SDJV4py9yClemHp0jMNYV9ztRtwtnbAhmWspFt5idezZVzUaFxW384zq7NwrxcCWADfiw1L8BUEsHCGQ+JSdMBQAAbQUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADE3MDY0YWZkMDI2YWRjYTYwNDRjMzRkOWU2YzRjYTUyXHI1LnBuZ32UeTjUCRjHR65xDMYxzahh52eUYyZH5Ejl+DFkhkljne0sIYSKYTCVyoQh5cq4jxxt27htYSjPSI4YlUiIIoasPI4c69jl2d3/9tk/3u/3eT7v93n/+74ssgMBJqksCYFAYHa2oNOue+wNdN+uplNC+BCIKMMOtKBEDs/nb9pTLBQ7FqhKmWUbHFK7pS4GGi2naCFq/Tq2NSHxLadVxQmbhvBesRSp07fHO70Au09rp7t2bxUnD2GfVN3JK+fOXePQI/hjLW1b1YwWxkKPIM8kzE8mzMA7Yqpvwb/hIeNBWVT99LvXxcIB7m92Ht1dnemhj+woI2I2h8fFJR21tFWq8MskUXTRzayP8OwoQ7OGmKpC86zAhfJkapOKsfpSTcXAyiabEWExVy4ubt7NmljUfC1aj1LKVza53vNOx5PlgmhbYUgrbBhV9Q1sS8afv65ZlwoFN2lW93FBnp4pCXeEJ3sdcUTPl0cGX5F9SHryMoitVt7qeglxrEVNVvUofAiKIuCOSh5CfzWEbBNEcqxi29eGMWy6i7L/KhxtxBzHVPK+21Y9epHeBcWBax25ygKWtIsqnA3BZUaJqjTOnJwuMgF0m7/c98u5RZ4df2Itd0Pg3RquJjWxBS8UEysw+okbs/6pFz1yaWF8jfNZv7LHpmQ2hKR7WTonu2vInT0rq+Dy3qWA7y5P1clgvtyM/o0WkCp/KxAKdeUifcDLA6vsyIvn+EtM418iDlY4lNVGApgsKSGhto7ImjDu+tLycileJvpDtq9b8kZjRfvttUFOiIfzEKV6KSgCsa3kdBomI6sO3mVZ2LQPwyTutRTTqZ1d33DaehU5Td32lVNTTsdtvo3bC+2lDu7Aa9yhYElpNjs004NTmyu1/CJYkCQJjD/TzNNvyUw5DlziqqZrTIzj38dP+X7XzmTlYqyc7Q1F5UMJIuUeZvuH/bko4TLnYBLFthMNXyGZrQz+CngA82WYK2FtTaHW4N88eCyEHZf3+4c3M84geJs5Cm98Fl4XOZNPrgmWKnppQFOCn8Fg6KDKwEDi4TGNnqfXtufJNQ2obyUAoIX9chdafmSR7Ko5pDWH8Ox9BTeK/ZdP43O29ArdmlWEcymUj8qEvdMWqKaBQwUeXJoEh86jW8XroRNHqmecBAWPUlIuAhrBXPqb/gOhLq3UOKrG9NWrmWgQV5NhytHCZkjDaWlEZWeDTpqoGM6QsW/stAYKcMjM9S8LnCdji7+wEvASrppZIdHa7oNRSyJ5c+8WlKLUi63hn380S02pSojkbhyUk0gQAfcBAQ5MRyzxFDwkVbcXRNrwaPJeSIl+O6YXlngYHrcHG6x5KwqfERL9jkyPf5Lb/wURJ7Uf2yLZ4bBdlQJGAS/PVcI6yEPOF9ckMkU3OUKpN2zNsT/wkqFPFQhJlxyXwIZ2t+ZAx7Q9Nwty1N9zWkEVazGpzv8ktQ3Pf/DnVdhT46SdZcPRCdwffe8vJ9XNnPr/xepV2BSsmh/UjudPRDF2pmBIU1qrV4hEyBWE7MjRAyzyMbXJ742mi+qj/cGPH3MmcCpPBAKBXXeyH7He4Gx0c7tO61nVC4ulJzKkZOSkecu7fW1rpu7mCurjiR3sSvGwxsrOBlPi6GTd0vmtE9nOyAwTYJKUXI4LQDlrHH7YqW5MwJou5789w+P4KMqYXAMy1G3cRKbqk6ibm/oXmlO0yMe6ogAkLqN+zc7X+pC5kMzS2cWbtZOoWrYlfX2s27s6JeJTLFLHD+CdSS1uPXclDYtvkURoh0af/wRBb4ipjRUaTjWL7TfWnS3o27+d89XfqCw6bt133pYIDin2GEupW4sXrXQrOnbZkMLrpym8nhyp6aSOj6H6PoVld+65wBhAqY6rEG/kIfZ5gLueua5P3pbHzef8rLcowYBszO43hthZO4CVlj/f+gtQSwcIm4KhdKcFAAC0BQAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAANzcwOGVkZjA5MmMyMWM5YzRmMjRjMmQ5NzkyMzI0MTlccjYucG5nlVT5UxIIFGa9QlFLSTGPJDKPMlPbQm0bLzoQ82RHVDwyLC0PsDLzKtlSEExJrEg0RSVpVUwoUnPNvFBRwmO8MguVcTex8Danddndv6Af3vvmvfnm+968mffIfj5ndLSMtQAAgA7yLCJAiaH/BlBFmQvRCQMAgLobEuGOTpmQl3xH7XY36l7n6g8Npvc0oW1VQHfKIERYdRmwBphbPd+v3XAfQasBegYirFFp/hRtTkH4C0daxbC5Cxkl/dYrHOLfEDQvnpwckPfbu76v5YlF6TLGpVLnlL15j8I2vx8yzhyGJ7dEz4o4n34biQ1x+Ju8WDcv4svTdSitGSamgLs5RZ9TR+k72ETdd5EMyBmcbKQPsrWuoXmHs5Y44TR+VWxDE9cKvL+4TvNAIfDVKGAl07rURb3ptkNFVAA33/xoP8hXWtRp35IfD2tdZr+UXXIyBXkxKIh6fv7vx4WUvBwkWehUP03seNsxN1VFcdwdHEi9U6x+BDNWGklXnJAvrTmAs/IKCB2OFR/flQervnNFlDnzg1W4Zkmb+BelPuYOBM8NM6kNNn/FxQuju79+15B5fEIIdGlJeF4BfBPFCPpIo/w5o/3YSqUdFR7LtgEWtcWHqv2UYqeBhTdAB06l7zFOnRgeuzn/pt9scnLtS1rALXVfGUtyTWA55qRRIsLF1fYNP32evVr0lMeTXgmLjblWdsvf8xOsmGVanX37djPF/bSab/w0gnvsJgosLZvIWCEVluNp0TTVq/ugkVtG4uQESMTF1nuT0rKBgTkc3EA2fdBmEdPy7Ho04apkablxfCWoZnB7X98rj9lHRjh0zVTB12bB8I2w8MWppYChWs5TFv859EmXoonXfqWBesjCZLQVUWOnIrGOlc29rjIULDyQqkgW3uayhOtfPtCisfvgiA/rq4MBHeuHR7cM5iAP50hdGM98oWNdAQpmP+Vhx5esdRtZxzuGzcH6DnSf1BOdA7a0JN09TKtrKIjBtr58u78Bm/Qe3PbecCE5WNiTmMxPO/kfk3YlFA4ql5frT+q55cV+TkU8QN1Lg+28PKBFhueC4psTQUWkLrz5/2Q90zAP65rdcUWrQGOtJcQF/ArJ9qHpOgKfIPmUvyxipcXFBUhSdj6m/Nf1y04UaDVeeohrS7VaMHGhzvj93F7Vd0I5SACMONiUBkFyxREat/ZkljstK4KTdxE6vWS6zwui6YX6et73vY1/1RauqGmIUo9hhI69BN+OnuvgCr68WCnORJNJTywiqyKbOEHUhcUeML6uBIQsseUy6SS8gaHSgQ5lyfLFj0mWLHIM7Afg7Gl9fwu7bH/lDrw6O+17CUjEi1dGXRvGcASaQlEc/cOSHY6lihXHnnV2bphHVIRgqds/UqSYRHjeVK05GsoxhLTvjViGJ7752nY5p/GAUv08lau8IutimoL98nS6putfPEtWCFb7Qnr/wiihN+8iNSyxfCWFsw39uj0ThZn1s3NysweKZ57p6C5n2hhA2mE53t04ccsmNgiHNbNc1MRsOnyjiQ5q9/5Ck8gsAx/wqQfphYGz+kwr/RIG+xrd/tCeu54+T4DRZH9Dd2e5VNCWJRo/UqlFP5eUBTwOOiDPwDTagcsAOzY5G27jCu1xVLlhlqBhzLbSbAO6RmGQ8GicNT6IaYFEcYl9ucwPRk5uZxIiO7Z4bOboR5UdllPLm1Hh4KkwNlqMyQw+oQ/WO65u5dNQOQ+ghzOkNuPVnHtM5yJ73sXBdEXMYStPXUzvRspIvZXHN6IJ9HWG11Ix28BELbSrp9VgQ5UQPcKIK7ivqXypAOQpH0SdRyTxH1BLBwjNms5SVgUAAHkFAABQSwMEFAAICAgA9n15PwAAAAAAAAAAAAAAACcAAAA5OTBjMDdhMWJkYTFlOTlhOTMyNGQ0ZTlmOGZjZTc4MVxiMi5wbmcBAwX8+olQTkcNChoKAAAADUlIRFIAAABbAAAAWwgCAAAAk1RuzgAABMpJREFUeNrtnftLVEEUx++fFYJSWJbYg36QQMgkNEGN7IFG9pJQsLRc0MxSRFO0h4qZWcbmq1DyVSkaJiYq5iuLVESX2L7LLGfHu+veq+0FZ3aG+WH3eq94PvfMOWcGzlfNaTTWHX87Bmer28Zza4cyyvsFnfj7m3uml5bXDe3V/Pyse2QeFKKzWo9l2qWZoAM0eM3bIzL4fSmttFcmELoZl9dpH5gxS+R554Tu+dTij/C6vm+LIGXG8XbPgC/gb8aEUdlPvujswhVvZ9F0z2OZ8M/YGobnfq05ZRkraw682picdv5l4+KWRHgcWG8ysdBxKWr6ykPhPUXzuVjwgJ/YI8d40TXJLx89EcQIHoczOAaSDlkNQJuIwHNosUjvHfwoeTNK2YcZrrG6g11F6SFWKglIMgILZn6FfcxNJLPqE7sEYM7gG6jImfnIQS4iCLxUlQabg9BIsH1gBFC5aCjdKIKY/xV9w5Pljd3XChuTsmvS8+sf1b3HlfUNh+jRBAtHo8xMwdb/mJj5eSKtZM/J294zKqWw6/O4iETgGgwC9i4aBRFcNXwSfhF2+q5PHDRvPXwlnLMgXDAIWD5acmEX+zK1sGqIg8wOOZW3L6Us4kJN5OWGiItPw8+Wh8Tdo59iHQnnJlSYaBRU/JchoxNz5B2hCfePXH+t2zUdvdGyL7mUoLzsGBQ0uHqI+EvaGw6KHWFnivzsssPPPWa3HUi0Lf5ekZZIe+8oLRZv79g0b74NjS9gN2OVSUsEyZUZiXhheBiDsCJiNNkeEdjGjDx46Zkhkagrjezm4+eLpSUC25iRh682mTmzo/gqLZH4zEpmYWR6vSEOBBoKrtISya98x4zcn1plSORQWi27GQW+tERQXLgrkfgCZBP/RPYmufM0OEpLBJUFlWeoOPzgQOilICLWHmd7RDDq7ANuU2NzkV994kCUQcHCbsO2WOaa1X3yeMfz/sMSH2BHg8qdVWX4zJfw2ASLVbDukAiMpKTjmbG5uitIMSKeCeyEiJkDAfiRcN7xv0TYoRHyCJIrgYDv5JS1YPsjwcHiTojIfdSqiCgiiogioogoIoqIIqKIKCKKiCKiiCgiiogioogoIoqIIqKIKCKKiCKiiCgiiogioogoIorIrhqB6n2SgUhge5+EJxLw3iexiVjR+yQwEYt6n0QlYl3vk6hErOt9EpWIdb1PohKxrvdJVCLW9T6JSsS63idRiVjX+yQqEet6n0QlYl3vk4cI6QaIomxlUe+TRzcgo7zfvLbELhkB731aWXOQmpFmaxhmXzoGZ0UhEvDep6mFVdJG06rbxkkeT6YDgW31PpEWHCBohCcmp1043a9A9T5R6LAPzLi0rii4mhTukWyM//hDYRUBxUWkwj6mU0kLqkGanExL0EVkaXmd5CgRVoIKBy+fCGdxkoogL7vYPTIfPOuFXIHUJN1EsFhItDc6qzUYoAAH1an4QOp4Gl+l0B3SR1ksFvIOfGDrRU+EFSo8FJQrAhWyJgc2K7y8MXCADn+D5l3P6jSvwQUFjOh6vrCruWdaJ/WM1897h28iLKYg42wlig5AYinFk9iobubWDvlU1txSLx5382LIkknGe7uGMRHyF+wAUe2TyK+gEwsES8bMvxX4B9An0jII7Bk6AAAAAElFTkSuQmCCUEsHCLLR8sMIBQAAAwUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADg5ZjJhN2JkMTgyMTM5NTJlMDI0YTZjNGViYjM0NjhhXGIzLnBuZwFMBbP6iVBORw0KGgoAAAANSUhEUgAAAFsAAABbCAIAAACTVG7OAAAFE0lEQVR42u2d+0sUURTH588KIUksK+xBP0gg9CCsoAfZA43eEgWWlkJm9iC0RHuomL1jK61QSrPa0DDZxMKszCIVsSW2r9zl7HV2nRl1hvvYudwfdscZ8Xzm3HPOvV84GhG7MRH+1xIcrHkaKqp7v7/ytaITf/+9V1+GRyZs7TUsftbW/R0Uso49WVkQ0GaCDtDgNc+MSPDTcN6ldp1AmOb64meBzgGnRG4+6zM9n1vxEl7X8XEIpJw4njwDvoC/GRNGHb/2zmQXrsQ7i2F6HsuEf6a0sevbr/GILmN0PIxXm13YzL9sXJyWCI8D600nFiYu5Xc+8FB4TzESLhY8YBF79Bi3Wvv55WMmghjB44gkx0DSIasBaAoReA4tFu29gx8XH/RQ9mGGG6zuYFdReqiVSlxJRmDBzK8K9EaJFFS/YZcALJJ8AxU5Mx85aJIIAi9VpcnmIDQ2lr5gBFC5GCjdKII4/xUdXf2VTW0Hy5q2HK/NL2m4UP8cVyb+hlWPJlg4BmVmCrbWo2/g5+q8i/PWnIifmdvKWt+GVCQC12AQsHcxKIjgqu2T8IvUDacS4qB59Pxd5ZwF4YJBwPIxtpa1si+ff4zZ4iCzU9YVp227nLGrdunexozd19O3V6asP00/xTpSzk2oMDEoqFiXIT1938g75m88u/zQfdOuacXhh2lbLxGU2y1BRYNrjIhV0v4bptiRuqncYpedvuMKu23R5tKh36PaEmlu76HFEu8dU+aRR/NzzrCbscq0JYLkyoxEvLA9jEFYUTGazIwIbGNGLt5zw5ZI5r4mdvOqnRXaEoFtzMhlB+44ObOj+KotkZyCq8zCpfkNtjgQaCi4akuk5OpjZuTC3GpbIkvy6tjNKPC1JYLiIlqJ5JxBNrEmsmBLNE+Do7ZEUFlQeYaKwwIHQi8FEbX2ODMjglEf6IyaurYI+TUhDkQZFCzsNmyLda5ZoyePJ2PvP3XzOexoULmzqgyf+RIem2C1CtZZEoGRlHRic22R6QpSjIpnArMh4uRAAH6knHfMlQg7NEIeQXIlEPCdwssPsf3R4GBxNkT0Pmr1ifhEfCI+EZ+IZkTkUcLEE5FNCRNMREIlTCQROZUwYUSkVcLEEJFZCRNDRGYlTAwRmZUwMURkVsLEEJFZCRNDRGYlTAwRmZUwMURkVsLEEJFZCRNWs0qrhInc18iphIkkIqcSJv58RDYlTIozNKmUMP+c1SfiE/GJ+ER8ItZj7rqPPkTc0n00IeKi7qMDEXd1H+WJuK77qE3EC91HbSJe6D5qE/FC91GbiBe6j9pEvNB91Cbihe6jNhEvdB+1iXih+6hNxAvdJ0aE+gao1dnKdd0n1jdgf+Vr570lpBou6j6j42HqZmSUNnaxLy3BQbWIuKj7fP4xRr3RjJqnIWqPp9+BgEPdh3rBAYJBeLILmxXt+zV33YdCR6BzYLLXFQVXh417NBuhr38orCKgTBKpCvSauqQl1aCenKyX4CSR4ZEJakeJsJJUOPj2iXCWCHUR5NsutnV/T571Qq5A3SSjRLBYqGlv1rEnyQAFOKhOxQfqjmfwVQrdoX2UxWIh78AHtl7MRFihwkNBuaJcIWs7sFnh2xsDB+jwNxjx9ayp5zW4oIBRvZ8v7Lr36oup1TNeP+8diYmwmIKMM11TdABSq1M8NRs1zaK69wk7a07bLx53882QNWsZH+8a9kTIX7ADRLVPTX4VnVggWDJO/q3Af6WXA3GFz2jzAAAAAElFTkSuQmCCUEsHCKCHXJFRBQAATAUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADk5ZmIwYzI3ZmFjNDM0Y2Q0M2Y0ZDU3MDY0NTUzMjJiXGI0LnBuZ+sM8HPn5ZLiYmBg4PX0cAkC0tEgzMEEJCeH5J1jYGA193RxDKm49Xbub+8QR5Hj7+eLNk2KmHajuW6CwgvHiCaxm8zd94RYp9mynJ3XsiyFX3hzec5SUa+fK3h4hYVFTxt1G6VEJ/3W2yyzfPfr2jf3blpXl7f9TPz+7o618fziZ2dmcj9fI2ai/e/A/W33zofP45tqvu928OW5S0Qf7/+elfNq+v2SfbMO5sv+jXdQfP9h8tOldudDLjBKddyUm3ivP1hV3Hovi1P4ddn6Z68lt3s9ObY58e7fo+nxTq932fk0TRE9Onm5g7hBWojPqxNXt++qfOi1ZFPGrt8bfX5Ua836rbbvPMveoGXpTAJvV20Ki7uxw0JdUI792uzpES92hNyvPO/80NS1e1dEQXPj249uO6/aHdKXtxW8wSHnbmDKZSY7y5ThrzvLLOfuo59vHZzOzc+W8T1R+PqM+wfXHfrqsW7tkYlnOXRufMmubU5UWvp1/U1VBu5lcY3u55b122q4sLRN33MpJFhAS1orzoDpQ4zJjrwUxzX2i1bnL1m2NDk+1PvhxLa5y2edu1/Tp/3PvjFlu1qEhdTbMyk5vac//Ng+VVX82Vo7qchi89Ct+yWLUr0KvThWHVR48GbRRMGDoZetL2Yf+yUcWBhgW/IuT2nqUUHOgzEGHBF2UYGh1r+Nfn3drsn3Sif37cczvtM3bTd98ibr3L063exi31u7Jn/RXjJFQobPq0NGuLena6O0kYGNY+3yfIu9Jf9r767MvNnYPtNVPFNm++0q4YbDjpyC7ZFKbrO/zWfITDt2LKs5uOzatNNrbh5q6jopf/lRgYWeYrVLlDW7h8jE2v/h/HZe59en9Co6B+ZNZeC8qcx0+ew87lyTWknmpaK5vi4eJ+QEz/Tallzse73Mpah8+4Zj2tvmibq4tLS8ETx454bz9Dd7k5/OlV0b5+gCUjvxzyWrbxfmzPVdptwgdfkSVKFl6PcZtoWOhXszv3d7S0Um7+hv6uiYMMFW6cauQ79j6lRzpn7keCbeVs5YIAI1eZ/rbPtvxs3vNm7wdD06txDsjCmz9837EHJ9yuEq97fSVj1vJ5geXug9p1rNyWlbZ8s9G7nZtVVuByV/nP7AfXNe//k9zR3K0wLaQ1takhSbPCd5zl6bfao0POGA0Ge/A5GcR52OnCoUXiyyVrZJRcRa8JsXUxjXstlVR0+c0rNtKZ77o9zVz1NDT2mTqLvKE02lc/tqwlxEBF1dBANJoIImdeQIun/sVy9T2uQqY2k6T6LzhFjhkwcVSYpK0Ucmzv5o6vhTqS+mb/1E3Ucn/v6QuqnUd6efBI5HTg3vU16DczmqoUcmdnw884z3RvDlXMPtLSGC7uf60qvUHG72bOl6Zvdt6drvm1eu8xIF2e22/9+yOxm3pi53niKn/4+5Qkm5T0aG/2kTM0vvhzVa2VtnfPde1aHsfsx52eHrxnKnSl2PXU16JNc/daG//ck1hxa0dFz5xVYaeSloVYCf3zRvA5eUV9PnXwo8tGaJCJ9drdIUVY9Ilp9buoGlQlD63glaAWYnDQR1xLxuzS7/4anlwMj3Kfhj46bHmXumO+na5KdujPCw/tC4VtxW8NmKDwEP1kV4TpoWw9ouarfXsKCB775D95f0Usv1B1n5fDY9/3x0z7u9UpeXVrX9qHzb4ddyU+SNRbGqK/uCJ6dE/E+6lW7d8zH2yplZxc+63bPtJDcdDzrmvqrNUvCS+ByGh2+DJ91XWRuhEGEU9i/sgfwiM5OFk2P0TYElKYOnq5/LOqeEJgBQSwcIsyYwX0oFAABwBQAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAAYjMxNjQ3MzhlN2Q2YjgwYzc1NWEzMzEzMDRkZTNmMzVcYjUucG5nfVR7PBMIHJ8Vx7BsiKldbmbovDqUV55bbcirYaKRUHqseV1kIc/Z8lh6eA4V1ZHXYh6xQyimxTqEiFCuWTmaOOPm7v68z/3x+31/n+/v+3v88/tluLseVQRpgAAAgCIOi/aUoN+2yQIlPhdPegkASMfj0Pb4mLHF4j+d8fYqvZ9LVO09VyrUxErXXiXXJv105S6jDQnS/zG1Sh8jsHdTNIlT9wtLHervqzU+8Mi4v14XE5Wx2MqNKBJWr9ZNvrGIWwUvdwm/CttMSiLnufkW3EHq6C3Gl6l5Ubv8rhb6+UkVPAfLp4mmrqzHvuNRLyYo0jkN7WIZkLNoKgCv/scxaXjptby3kLAt4xyfNa6bpkv03HR6WSPxAbraRnBAHH98Tfns2+XVKfu+jJklvVfST2CqxZbkhYZHAU3QGv20hVV11B+XnD5Ztm/uzfpWrgBO/2FMcBflO9pkbgiBfddTWELIayo6G6PjyDDrxpoTvuyQH3+fHdE2d8+awkUHagXvZXB186IejgBW9kHOghV3T51P998vjBoSaFmSZDmO/qmfGMTjGTq5EAJVWCIX3U1VYSboGUoRkMsg64jBq1x7D4Tx09lboQVJ7r4n1wlKiR+Cfo3Wkp/ZgPCsbLxH2ML9lQGX3wXFv2jgN2STQ4JNi4TDO3f0lubnX38cvbAgrjOtCRqqT16KJpJ8+ytJBicLSlNKNYDAYUMZGMS/Qaw9WdDwO9ZhL361uCXfKWQJ7WCsBgSmZde1V2Eoa69tg+nJxIOx3dNhzV6sRv+i1jbS8HA//xDejRh7cxOkVy6Tng5F9D7TvBe0mBYlopRfdvO9SukQjld48TsPZ/KHfTytSKbsB4BtGfg0ugq1OGgcFjpcoLy7UrCwh0cbD602EG+ed4eDedqzWVg+yxWK2Wjdqoz77PrCAkVKU/Bq9gIhZ7NkXdgxhk8GfzaRcaocK3iYk2OF+FgY81Fw0edCBnfcw4hEfNrsD4GoQiOO7ryqvKuYw+p4wYRnEjFoPPY5nFHUGTlTFrlc86YRcM7F0ecf4f3ZicNLz2CFL8fb412JmU0w4T0EYv/2sIrqUes7kQqNfS3Sx0e6Q6XIeDQ6NWUC0vEUk2s7b0IfOR2YS/vF7/3fe+g2lDUSfO6odV3RoRyKUueXNSnSDaOF+SC5ZhT0bay1qWilqkFn2qjLSCXSxqYfjLhNcIJ7q0Kd0mQtcaiLVYZGB09ek3IeYCayJRw1dw514tEJKxWcbiwiyBnoDaoonKTdVvUy62x2FRMZPtACJQipW1lujUZlF/KkGIlYO6TmjXn0N3TnivL0bjm+S8oppIsOJI1hXIxWP9IZBT2lvk36IV1sISSGsRjdhPlX6fYf5OlpVj0tJdx3pJaWUqfZaQDtCUlIcUNeH/xeoxJLqOVpKMlRd6KBiAkq2SrcdEmElDQp6q4UIXHb2CVCOkoQ82GtQJZjTp9fNpuY0V/njZDprI+2AV0GL+9uURTZ5vTN/0+c4424TwI+cb0lMZN9Rv+Snf1X+fRm7aZuX+sLvHfkvHoYrDwaPuMcGVfyuLqexooZZbqJHW/uGWj6Ulo49P4YRYq5bk7XWSzzJycGKjElJ5seyyFIqsN25We5+10yHVGF+aRnxFG8WzgbKBYoGaodgXod0nfjtkdqRATNP8kDsSPhiC5cm+t0ZDqHr+Pgi7iJcXdtHV0X+c1fV/OU7kPBtJI6HHBxdwScEjn3xOQNPKVUEJMmKH8Fb2fXq+vfh3/T7KHnU8n4YF2yTxES51yT1E0rmlQ3tzva3kFdPXPMoqZDGuzS8mEZwyEdFl9w+qqw1D/GyKPW6uWF9zjTwHYLt/SYNzILzoUPFKbkm/UOqGW3zgU/t3GG7avREKGxAbXAFLYbLp7/JCgx8Ln5Ghu4BWD+FjLIEgDhkocMwGFc0dUOgUl/AVBLBwhjBFZxqgUAALcFAABQSwMEFAAICAgA9n15PwAAAAAAAAAAAAAAACcAAAA4Y2RiNDdmN2QyODE2YzE5YTc0NGU2OTFkMjE3YTE0MVxiNi5wbmeVVPs70wsYX6LkNqtc5thDK/e1zjhuCc/ahVnN9WD5dlzaShkxI7IUimklVllGz0HmdA6G5JZOKbkNk6VcJmvtcOSaO5WcdfoL+uF9P8/7eZ/P+3l/ed9ML5KbppqBGggE0iS4Y30UGPQtVJUU+aZflAgEUsESsGi/hOGZu5+Jfujd7XO/66A5gf6DacnZxhPowBRd576J/d4hQ5iOaQIN/CDj6pBTnViNz70dGvqAcIWah4OGEWlSaq6ccW51VPI2tqnm3Kk7RvFzo0knx21OiQoao0UGqCZrg423b5bnu++6x7WwNYvMyMf6NsvAUvCGfi2sMnQ+qL3Ls9Dr8cZKuTA6xHICpFm6LmUx/oZauq6YuxsfiZPNNslEyX9gkSMzNs5PF15uDX8rH0gzHsPO91u8VFmC6qQNx6w0ngYaOOWI9A+JiF3rebzx2ZTKvdWFt2Q55qXxUb+WHRpquJPLurZ1ar874ggwiXzKKerghZUAiITm5yvK9wDaRasDRjaQQVWoG8JezQ5mYAvawCnzMGyTj8N7uPcGksJXIVvtL0v3CJ4vdwgqLlNtlNRRX3bJRpVzhK88W01A7LHfUtyQ6TeczUnK6dzHYsBX25IdMauu9BHQaIiioAvYCSMbdv3i6j/r+Ay3C61PSvdeX42mLgX8IqnYoZuFdrKBBk2JBzappPW+mMV404Fiau1ML3yzXwf5ACpMOaOq6tCkT8FGv14hPOTVh3t6GPrVw568L7ECKOR/mgFV1UAXPDmyaW1hdtEzyLB/cE2laZELOwAcd408Hivjxap0YeR6s/xgFHEzAyHXyDkRlu1dHY85/2nb/ZkdbHD3ILOHcYbXOIZPHkJNtvPrkJWd1qJsGtDOCowcflpckpdInESQhlSsSFclpgcqoF/spmHkNigdU7LsDT6Ko0suvq6wN7s1rWd/QssZ3uWAQWY2M9QbX+IlXJTXMOOREJdLzEqC6+drH6TOJAbBcVNBL3pqAmALLATXcBX7s90exqe2LtLoUN/k8nfKw9JzR9ErSx4tCWRbyp+CkJGOs5nTTnFE94KHCw8jF327fnrRE22kMDNpd4bQjmdeEFBcabfjwKa5pvFbope+T6k62zd+Y6O7OBFB8+mjgHns/1kvg5a7mUWiyvRl0pAdQ19S1KCZgZzroHd2sty/9MgFqA+JRPDz4PRg8xUmMxeGNawWN2IQFOgYBauctu+mnf+/AfmC5kvk3m3qZLxiLQfHqGJuXWRszhjnpgVk3kPJX600/xiu968s6aXYGcB9nJKokF4uq8oe49xThtgGu0TAeSzT4szwHwBHAjanQf+bnbmOXot5uwnk9fswfXnEiLb3fmRb7xrvzvkYlEv7wH1dPflF5vUzMaivP1REMjXHNKtENP4xQCOJ2RM4eklxq1qxREWvRT/Y5tBOPg2PPxpbvyZ+s9zHYymE1+Zt51w2S0bC2/KcIB43uOvqKZtGei3wDPqzLanohHH/2oPdn/l+gAbb0BomE31NEFhZC7R2rSqXY12YZjVqaTvN6PCRCCEn1/cKnX4VSI2BY1zxFjCTbg+SLPuV2WFy2C2cF6lpcH7Bd7Zcz0dFaJpnnNp6mJDErpeKVMyb0cmWLl7xhzArPhNZzUFkhK5Yi6k91XoE62BpvbvBisQpoQY8C8WRzmoYFu6Vhuz7XFNaMPBOabupZHE9DAgwemLPP9+21DWcw2NVWQzGiE1w2wunhbs9O/FHax/JcMJu3unFVnmUI5Te7NNmVpbuDBHrFYBkM74cKaIi0DjQmvTV/x04n8Hdku59kql4qyACjoQVHA5J/Q9QSwcIMAYiNFIFAAB9BQAAUEsDBBQACAgIAPZ9eT8AAAAAAAAAAAAAAAAnAAAANTMwNzM0ZTRmNzAzOTQyMWI5Nzg2M2Q0ZGJlYjk5MjBccjEucG5nAasEVPuJUE5HDQoaCgAAAA1JSERSAAAAWwAAAFsIAgAAAJNUbs4AAARySURBVHja7Z39S1NRGMfvXyWmqalTWyoWgglC0AuBEVhQCGYERlSYtgy0GokiaSGKpoiglm+pRYqYiFk5S0WGbz80iSWxvuPI4+lubitiL+c8h/PDdjwX9nzu83Yul6+GJ9j49dPtHBlytDTPVVVOl5fF6MTvX+3tcW9vBbXXCPC39YlxUBguyB88nqvMBB2gwW3+OyLbH2amSq+oBMI0x06fWhvoD5XI17ZW0/XvL5fA6zanJkEqFMeLngFfwG/GhFGzt2+Z7MKKr7MYpusRJvI18zW2H06nR5Wx63Lh1o4WFco3G4sHEpFxIN5UYmHisvCoVoYie4rhN1hwQYDco8ZYftkph4+ZCHKEjMOjx0DRIasB6A8i8BwKFuW9Qx6fn9qp+gjDDdF3iFW0HrFVSv5LMQILYf5iU+MekZmKG2IJwDz6DXTkwnzUIC8RJF7qSnVzEBoT588KAuhcDLRulEE8ug7KJggcgyozJVsNB1xDQMDZxaAkglVtiSBdCAgIH+PdxWLxZWdl2aPxoMbEoKSiVRsSILnuE/HoPZgIE2EiTISJMBEmwkSYCBNhIkyEiTARJsJEmAgTYSLRTuTb5OTbxobu69deXCjuKL36xv4EK7tut45ENpcc9ScL7sXH+c66bOvi+JheROAXtuTDfnHQ7L1ZEX5niQwR4CCz7yfEN6altGZauo4dbcuyNKUfeZAYT39FHKlPxLnwkbyjLjmxLzfb9J7cQF52Q2oKQZnt7lKZCKKAcsfj5MMB3qtstqSKbQ8z0l0bG8oS+TQ0SMHi6x3yfJWXW5uUIDYjypQlguIqjES+CPr6LdJK+LNJuInANmFke1ZGUCI9OVax2X4iT1kisG2vsuZYQ3lLm/KrskSenTsjLOy0ZgbFgURDyVVZIq9t1cLI55a0oEQ6rJliMxp8ZYmguRBGoo6gmgQmUp+aLDaDo7JE0FlQe4aOIwAOpF5KIuE840SgZ51ubxN2Vh+KQ331iwNZBg2L2IZjsfrnmrZLJXT/7SlJONGgcxddGT7LLTwOweFsWCNGBEZS0aEJlzGtoMSE/5lAJJ+PBH4gAD8Ks3dExTO0zSUH6giKK4GA7/TdvYPjj75PFaNtMBEmwkSYCBNhIkyEiTARJsJEmAgTYSJMhIkwESbCRJjIvxIh3QBVla1CHPu6AdPlZawtsetykZqRMV9jE1+cI0PaEtlZWSZtNMPR0kzyeNoSIS04QDAIz2hRobaCG5Q61gb6vVpXlFz1FO75vviF0ioSipfIYlOjSSVNq0GanEJL0EvEvb1FcpRIK1rhkOUT4SweUhGUZRfXJ8b1iRdyBVKT3COCYCHR3uGCfB2gAAf1qfhA6niG3KXQDuWzLIKFvAMfRLyYiYhGRYaCdkW9RhaHFVneGDhAR95g+PazJs1rcEEDE+unHti12ttjknrG7Ze9wz8RkVNQcQ4SRQeg2FKKJ7FR05yrqvSrrHmgXjx2y2LIiknG+7pGcCLkLzgBotsnkd8YnQgQhEwo/1bgN1iCxBmHToEvAAAAAElFTkSuQmCCUEsHCEBBjFiwBAAAqwQAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAAGJlZGFjY2I3NDEyYWM0MmY0ZGZmYjI3MDA1ZDNhMTdiXHIyLnBuZwEBBf76iVBORw0KGgoAAAANSUhEUgAAAFsAAABbCAIAAACTVG7OAAAEyElEQVR42u2d7UtUQRTG718l5suaumqbioVgghD0QmAEFhSCGYERFaZtBlotiSJpISuaIoJavqUWKWIiZrVWKrL49qGV2CS2R0aO0911713bC87sDPNh9zpXPL975pwzF86jFjAaf377vcODCy3Ns1WVU+Vlgk78/cs93f7NDUN7tTA/Wx0fA4WhgvyBE7nSTNABGjzmyIhsfpyeLL0qEwjdHD1zeqW/zyyR7+5W3f0frpTA69YnJ0DKjOMdngFfwN+MCaNm7tzW2YUrwc6i6e7HNuHvmatx/vJ6A7KMbZ8Pj3akqJB/2Li4LxEeB/abTCx0XOYf1/JQeE/RQm4W3BAm9sgxFl918NtHTwQxgscRiI2BpENWA9A/ROA5tFmk9w5+fHnmouzDDNdY3cGuovQQK5VEJRmBBTPf09S4S2S64ia7BGCB2BuoyJn5yEE7RBB4qSqNNQehMX7hHCOAykVD6UYRxPyv+DEx8a6xoevG9ZcXi9tLr711PcWVbb9f9GiCjaNRZqZgG36sf1uoP1VwPz4ueNZlOzxjoyISgWswCDi7aBREcNXwTviF05YUEgfNnlsVwjkLwgWDgO2jvb9UzL5sLS0a4iCzHyTEN6altGbaO48fc2fZm9KPPkyMp59iHwnnJlSYaBRUwpch3vlP5B11tsTe3Gzdqak/L7shNYWgzHR1Chpc94iEOwj4/RQ7ntiSwpyym+2pbNmjjHTf2pq0RD4PDtBmCfYOfr7Oy61NTmCLscukJYLkyoxEvDB8GYOwImI0iYwIbGNGtmVlGBLpznGwxa6TedISgW27mTXHYeadHcVXaYk8P3+WWdjhyDTEgUBDwVVaIm+c1czIF/Y0QyLtjky2GAW+tERQXDAjkUeQTcITqU+1scXgKC0RVBZUnqHiCIMDoZeCiFhnnMiIYEy1uZmd1UfikF9D4kCUQcHCluFYLHPNyob7cgk9f1dKMk40qNxZVYbPfAmPQ7BYBesBicBISjo04TK6K0gxIr4TOAgRMy8E4EfCecf/EmEvjZBHkFwJBHyn995dHH8keLF4ECJyv2pVRBQRRUQRUUQUEUVEEVFEFBFFRBFRRBQRRUQRUUQUEUVEEVFEFBFFRBFRRBQRRUQRUUQUEUXkUI1o9T7JQCS6vU/CE4l675PYRKzofRKYiEW9T6ISsa73SVQi1vU+iUrEut4nUYlY1/skKhHrep9EJWJd75OoRKzrfRKViHW9T6ISsa73aY8I6QaIomxlUe/Tnm7AVHmZeW2JQzKi3vu07fORmpE2V+NkX7zDg6IQiXrv09bSImmjaQstzSSPJ9MLgYh6n0gLDhA0wjNSVCic7le0ep8odKz09+1oXVFwNSncI9n46flKYRUBZYeIp6lRp5IWU4M0OZmW4A4R/+YGyVEirMQUDl4+Ec4SIBVBXnZxdXwsdvYLuQKpSe4SwWYh0d6hgvxYgAIcVKfiA6njaXyVQiukj7LYLOQd+MD2i54IK1R4KChXBCpkTQ4cVnh5Y+AAHX6BFlzP6jSvwQUFjOh6vrBruadbJ/WMx897R2giLKYg4+wnig5AYinFk9iobs5WVYZU1txXLx6reTFkySTjg13DmAj5C06AqPZJ5FfQiQ2CLWPm3wr8BftAx5nV77daAAAAAElFTkSuQmCCUEsHCL9yNpoGBQAAAQUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAJwAAADU4M2UzODgyM2FlMTBhNDM4YjQ1NzZkN2U3MGM2MzA3XHIzLnBuZwFJBbb6iVBORw0KGgoAAAANSUhEUgAAAFsAAABbCAIAAACTVG7OAAAFEElEQVR42u2d7UsUURTG568Ss9TMtzYVC8ECIeiFwAgsKAQrgiIqzDIDrSRRJC1E0RQR1NLetEgREzErrVRk0fJDK7FJbI9cOd5m15lRd7gvO5f7YXb2juz5zbnnnnsfOBohu/b3T9D/sn+6sWG8rHTkQomiHb9/rqszuPTT1l7D4ruFwQFQeJGf17c/R5sOOkCD17w5IksfRoeLz+oEwtTfHDk839vjlMi35ibT8+/PFMHrfgwPgZQTx5OnwRfwm9Fh1Ni1qya7cCfcWQzT85gm/DMTFeW//f6QLm0lEMCrfVVwiH/ZuLkhER4H5ptOLExcJu9V8lB4TzEiThY8YBF79GgzT9v46WMmghjB4wjFRsOiQ1YD0H9E4Dk0WbT3Dr59flhNqw8z3GB5B7uL1EOtpSQqixFYMPOn6uvWiIxevsRuAVgo9hoycmY+1qBVIgi8lJXGmoNQGzxxjBFA5mIgdaMI4vxPfB8aeltX23Hx/JOTha3F515XP8CdlWBQ9WiCiWPQykzB1rr9+DpdczD/ZnxceK/K8k0NvFGRCFyDQcDexaAggru2T8IvypN2RcRBvevKZeWcBeGCQcD0Md6dKmQflmdnbHGQ2bcT4uv2JDdlpLXv29ucmVafuvvOznj6FvNIOTehxMSgoGKdhvgnP5J3VCXt7M7JMu2aenOzalOSCcpYR7uiwXWdiNVGIBik2HE/aZfFLrshLYUNu5ueGlhc1JbIp/4+mizh3sH3Z7k5lYkJbDBmmbZEsLgyIxEvbA9jEFZUjCabIwLbmJEtmem2RDqzfWxw9YFcbYnAtrWVNdvn5MyO4qu2RB4dP8osbPNl2OJAoKHgqi2R5+W3mJGP0/bYEmn1ZbDBSPC1JYLkghmJdQSriTWRmpQkNhgctSWCzILSM2QcFjgQeimIqLXH2RwRtJGWZmbnrR1xWF8j4kCUQcLChmFbrHPOylrz6SJ6/9XJidjRIHNnWRmu+RQem2C1EtYtEoGRtOhQh8uY7mCJUfFMYCtEnBwIwI+U847tEmGHRlhHsLgSCPhO943r2P5ocLC4FSJ6H7V6RDwiHhGPiEdEMyLyKGHiicimhAkmIqESJpKInEqYMCLSKmFiiMishIkhIrMSJoaIzEqYGCIyK2FiiMishIkhIrMSJoaIzEqYGCIyK2FiiMishAnLWaVVwkTua+RUwkQSkVMJE38+IpsSJsUZmlRKmHfO6hHxiHhEPCIeEeu2fd1HHyLR0n00IRJF3UcHItHVfZQnEnXdR20ibug+ahNxQ/dRm4gbuo/aRNzQfdQm4obuozYRN3QftYm4ofuoTcQN3UdtIm7oPutEqG6AWpWtoq77rNcNGLlQ4ry2hFQtirrPSiBA1YyMiYpy9sH/sl8tIlHUfZZnZ6g2mjHd2EDl8fQ7EHCo+1AtOEAwCM+rgkOK1v3avu5DoWO+t2e11hUFV4eFezRrv6a+UFhFQFklMlVfZ6qSFlONanKyWoKrRIJLP6kcJcJKTOHgyyfCWUJURZAvu7gwOBA784VcgapJrhHBZKGivS/y82IBCnBQnooLqo5n8FkKjdA+ymKykHfggs0XMxGWqPBQkK4ol8jaNmxW+PLGwAE6/AAjPJ811bwGFyQwqtfzhV1zXZ2mUs94/bx3RCbCYgpWnI2KogOQWpXiqdioqY+XlUasrLlhvXiM5osha1YyPtw17ImQv2AHiGyfivwq2jFBMGWc/FuBf4kNyxnndUuKAAAAAElFTkSuQmCCUEsHCDn4rdZOBQAASQUAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAAFgAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNLK81LLsnMz1NIT0/yz/PMyyzR0FSorgUAUEsHCNY3vbkZAAAAFwAAAFBLAwQUAAgICAD2fXk/AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVa647bxhX+7TzFgAXyp15pbhySjtZBnSCAAeeCbFoUrfpjbtQyS5EqL7tSkBfoU/Td+iQ9M0Pqaht2ZRXW7mrJ4Zw5t+/cuPbs6/WyRI+2aYu6uo3IBEfIVro2RbW4jfouv0mjr19+MVvYemFVI1FeN0vZ3UbcURYGjvBE5VypmzjHyQ1naXKTZZm8UTSmOpM2URmLEFq3xYuq/kEubbuS2t7pe7uUb2otOy/4vutWL6bTp6enyShqUjeL6WKhJuvWRAjUrNrbaLh5AewODj0xT04xJtO/fv8msL8pqraTlbYRcib0xcsvns2eisrUT+ipMN09mEFEhO5tsbh3NnFYTB3RChyysrorHm0LR/eW3uZuuYo8mazc/rNwh8qtOREyxWNhbHMb4QnPYpJRhhPhfycRqpvCVt1ASwaZ05Hb7LGwT4Gtu/MSeYS6ui6VdBzR778jiilGz92FhAuFixBhC4dnmIULDRceLnGg4eE4D6Q80PBAwwGxx6ItVGlvo1yWLXiwqPIG0Nuu225TWq/P8GBnPXkONrXFb0DMMIRJcDk8x/i5+wj4cLcxPTSS7Entmv4jhY4iOU4/XCQ9y1A2yiSZOJVJ43eYKd4jNNj9IXaSeM+1IMr/+M+JRPY+My8iUfD/i8TZdMyV2ZAeqL13tEP4dHbZuoRhGYozF/cExZAcMSIZEgmCPEAkRhzWKQR+gph7xhFDKcrgAWHIZ0TsdnniGQgUEyQ4SjASkEqIAHeOYoaIzySOIH+Qz0bITMqAIo5RDKcSx5A6HkwgLmDFUsRBMchnxOAM3IJoihhBzJ2jsTuRICqQcPwIdwkuUseSIgHyieMGiQxJHBIYiFPE3LmxkhXVqu8OnKKXZrzt6tXW+0ANJWhX6EJJOqiDz2alVLaE1nDnsEPoUZYuCbygvK46NMJGw7NFI1f3hW7vbNfBqRb9Kh/lG9nZ9XdA3Y6yPa2uq/anpu6+qct+WbUI6brEW53rkuzd063WsGB7G3x/I97bEHv3yVvl1rCD+taC/LppR3JpzGtHsasG4Mkfq3LzqrHyYVUXh2bMpr7LzGyvy8IUsvoLhKeT4vyCtk3HVaix6TCCR0XqxtxtWohZtP6bberb6CaOJ4zjbPwmcG4TtghnE5GS3TcA3mrp0o2nk1Sw7TeHVNy8fYtmQbR93CIk13Zn7KJxuby3eN2+qsvdI2//N3LV9Y2fF6AeNs6qP1WL0voY8bkMzVg/qHp9F4KDBV6/bFawGoxXC+93BNWAxjEQDFcVrp7Gqbalwp4Gewo8RlthtvvQcT2Fv6pw9VQQvkG1wVQymjniINdF62sYjoa8GeuTC37X2/uq6N6Mi67QDztT3YEf+qWyuxByBN8WYRAJE9ahGHJBMbPpUSTOHmxT2XIIfIC8r/s25PFeThiriyUsw8bgOOlA/TPoFJ4au2jsQC9LP7EFt/rdg5g+eexZfdfUy9fV4y8QMUcKzKajlrNWN8XKRSa4pVr0cgG22QoQhWbxYHeRaIpWQq8x+1xc3oJvtOsp4J7O+Q4yuu/uawgQiFwL9WgBZ6EgwY5L29IuYTBDnQ9N1XddXW0BCUviBz/nf1SrX6E0jv4fqPzCGwnb74hWJMvVvXSj4eCPUm5sc+Ahz+3HPG9th9ZuZADQNwAFT/f2v6/NsV8BNm8uVJFViJSVtSHIuiHf0ArE+XTdQ1z266IsZLMJ/HZWwAAeMBiqvUS3qJHQkCH4uidrq7+T5+IfX/6B4K/Uu7c0bEn0R6T8aogNqBtOVc/257os0beFHvAfgPAgLpfAE1V+cvjZs492jU1ib5uE7iAGt/fduKECs4HFCb5Vv7RNoXcAe76gTj94lY/4fAiU5FNqLj9Oc3mseXyW5na9amzr3ghHASAKHjr0AcMwK7xfI32sUfaJNYIZomODVl/+s6+7r+765QsUbkFLDZ+wCL/fprTjER0yfH9y7yXM+dl9kr1+gmrBjflu2ggvUXSYll3EeFIo8033k+u+yJUHCFRMWBYznqYsoTjzxeKGTBiDBcOUQRNNiXv1/G2/N+z8e+AXKCKLndGrQoeilxdQxkM0Cyot4znOKZGc8jxNM5NZqZmViTV5MldksqoW0TCCvpL6YdHUPWTDcavZs6TyDc27EGxi7g8Mm+DGPa0/EB6o/aYIldANbAO1RP/5178R+VAEycci+L/W34+Agh5DkWVY40QSZSSxWSYzRrnhNsvTXNskJXNFP18o6DVDwY6hSLOcykQZklKXjdRiyqXQ3CrFuEjlXLHPFwp2zVDw06zIFdY0yaXmjGvDWc5NnGDB45hRquaKfwIoDr/4hZDh14xMfIyMYkTwhKU2MUKlWCdxLBkjDHNjWc7iuYo/3ySJrxkKcVKvtFE8yRNDUyI0yWTCuRUZMZRAQ+HQOsS5UNBJdvglLoSMuGZkkmNkYoYTxi3PE8wyTonKklQww42yKssonjdnz1fiAkmirn++Sk/qlTVSa5VwQqGXUGgjea5ognFsmCSJmjdnz1eXg+Kq56vsJCtSZlmaUiYtwZKzVPE4ESaxCdYCMmbenD1fXQ6Kq56vCD7GAqeKqJQboiQRUJGUgIplbAxvm/ATs3lz9oB1OSyueqIiJ2/jxM21MjeYCmm0FJhzzTi8kMO7h5YxnTdnj1SXw+KqRypy8jqeJDi1JscZ1ZToTPOcck1NlmQUXsxJNm/Onqkuh8XnPURN9/+g7/+tbfifIi//C1BLBwjZPbIP/gcAAMYiAABQSwECFAAUAAgICAD2fXk/T3u8qbIEAACtBAAAJwAAAAAAAAAAAAAAAAAAAAAANjJhZTM0ZjBmMjFhNDI0Zjg4OWQ5ZWFjM2VhN2VkZjdcYjEucG5nUEsBAhQAFAAICAgA9n15P2Q+JSdMBQAAbQUAACcAAAAAAAAAAAAAAAAABwUAADA4YjFiODRkMWJhMTY5MjBiNjA3M2RlNTkzMDkzMDUzXHI0LnBuZ1BLAQIUABQACAgIAPZ9eT+bgqF0pwUAALQFAAAnAAAAAAAAAAAAAAAAAKgKAAAxNzA2NGFmZDAyNmFkY2E2MDQ0YzM0ZDllNmM0Y2E1MlxyNS5wbmdQSwECFAAUAAgICAD2fXk/zZrOUlYFAAB5BQAAJwAAAAAAAAAAAAAAAACkEAAANzcwOGVkZjA5MmMyMWM5YzRmMjRjMmQ5NzkyMzI0MTlccjYucG5nUEsBAhQAFAAICAgA9n15P7LR8sMIBQAAAwUAACcAAAAAAAAAAAAAAAAATxYAADk5MGMwN2ExYmRhMWU5OWE5MzI0ZDRlOWY4ZmNlNzgxXGIyLnBuZ1BLAQIUABQACAgIAPZ9eT+gh1yRUQUAAEwFAAAnAAAAAAAAAAAAAAAAAKwbAAA4OWYyYTdiZDE4MjEzOTUyZTAyNGE2YzRlYmIzNDY4YVxiMy5wbmdQSwECFAAUAAgICAD2fXk/syYwX0oFAABwBQAAJwAAAAAAAAAAAAAAAABSIQAAOTlmYjBjMjdmYWM0MzRjZDQzZjRkNTcwNjQ1NTMyMmJcYjQucG5nUEsBAhQAFAAICAgA9n15P2MEVnGqBQAAtwUAACcAAAAAAAAAAAAAAAAA8SYAAGIzMTY0NzM4ZTdkNmI4MGM3NTVhMzMxMzA0ZGUzZjM1XGI1LnBuZ1BLAQIUABQACAgIAPZ9eT8wBiI0UgUAAH0FAAAnAAAAAAAAAAAAAAAAAPAsAAA4Y2RiNDdmN2QyODE2YzE5YTc0NGU2OTFkMjE3YTE0MVxiNi5wbmdQSwECFAAUAAgICAD2fXk/QEGMWLAEAACrBAAAJwAAAAAAAAAAAAAAAACXMgAANTMwNzM0ZTRmNzAzOTQyMWI5Nzg2M2Q0ZGJlYjk5MjBccjEucG5nUEsBAhQAFAAICAgA9n15P79yNpoGBQAAAQUAACcAAAAAAAAAAAAAAAAAnDcAAGJlZGFjY2I3NDEyYWM0MmY0ZGZmYjI3MDA1ZDNhMTdiXHIyLnBuZ1BLAQIUABQACAgIAPZ9eT85+K3WTgUAAEkFAAAnAAAAAAAAAAAAAAAAAPc8AAA1ODNlMzg4MjNhZTEwYTQzOGI0NTc2ZDdlNzBjNjMwN1xyMy5wbmdQSwECFAAUAAgICAD2fXk/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAACaQgAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAPZ9eT/ZPbIP/gcAAMYiAAAMAAAAAAAAAAAAAAAAAPdCAABnZW9nZWJyYS54bWxQSwUGAAAAAA4ADgB6BAAAL0sAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Mikael Bondestam om träddiagram för händelser i flera steg:
Beroende händelser i flera steg, 256-258
ti
MB
Komplementhändelse, 259-260
ti
<ggb_applet width="835" height="381" version="4.0" ggbBase64="UEsDBBQACAgIAJpaeT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAJpaeT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVfrb9s2EP/c/hUHfWqBxCZFvVzYLdoCxQKk3YB0w7APAyiJttnIoibSr6J//I6kJMvJ2qXtMNSIw9fxnr+7o+cvDpsKdqLVUtWLgE5IAKIuVCnr1SLYmuVlFrx4/ni+Emol8pbDUrUbbhZBZClliVcoFwVl5HJGl/FllC9xNpvRS5rneTYrymRZlAHAQctntXrHN0I3vBA3xVps+LUquHGC18Y0z6bT/X4/6UVNVLuarlb55KCRAapZ60XQTZ4hu7NLe+bIQ0Lo9Pe31579pay14XUhArAmbOXzx4/me1mXag97WZr1IsgiFsBayNUabYppEsDUEjXokEYURu6ExqujpbPZbJrAkfHanj/yM6gGcwIo5U6Wol0EZBJGEUtiltCMMJJFYQCqlaI2HS3tZE57bvOdFHvP1s6cxCgAo1SVc8sRPn2CkIQELuxA/RDikCT+iPg9wvwQ+iHyQ+xpIn898qSRp4k8jXXKTmqZV2IRLHml0YOyXrYYvWGtzbESTp9u42Q9vUCbtPyIxIwgTLzLcZ+QC/tN8BvZg+m5kXQk1bTbrxTai0zC6OEiw+8RyXqRIUnuiwzjz1iZfMG5XoeHmEnjkWdRlPtz33sSWfgVEv36+wQm0f9i4nzaZ8q8Sw7Qa0vbRdKIjbbpwmYQzyzqKcSYGkmKII+BznBIQ8BkABpDFOOSZpDYMQWW4kEEDDKwdJSBy404w39R6pglECMzu5tiSgJFQRHEDKhLqQgwkcClJaZoyJAijiHGS1Y8DS0LlkCU4IplEKGONiNTioQML+IaxYfAKDB7maYQJpBYfjSymZ5kVnVkGUJCIKGWISY1JrRPZqTPgFlr+qom62ZrzlxUbMp+alQzxAKpsRydip4vT2c18dG84rmosE3c2EgC7HhlM8IJWqraQB/E0O+tWt6sZaFvhDF4S8MHvuPX3IjDG6TWvWxHW6ha/9Iq81pV202tAQpVkUFnVdHRPBy0xgUbHUTjg3h0kIzm6T/KVXgCWy1Qvmp1T87L8spSnEoDevLnujq+agW/bZQ8N2M+dR1nLrZFJUvJ698QrFaK9Qv0DchVq74BsYT1iqi2vDlqRDAc/hCtwhoTTWZnH4zq0R8xmk3I6IMcdcFt7sWTJKRJNCNROqMpFnu80x2FWTJJSUojEiZZSBmNvWixGyLED2IwftXKcjy/0q9UVQ6ucNa/5o3Ztu7lgKWxtTa9rFeVcAhxeY1tubjN1eHGQ4N5Xu+PDa6Il5+vnNcBK0MYx0jQjbkfHY1VbKAijoY4CtJjTZbDOZ2FjsKNuR8dFYLXq9YZSnsrKenFSO3qGQnOssYh3zb5bS3Ndb8wsrg9WWrp3203uRjwc86S/kcs59M7+JrfirYWVQdnDORWbbXPzhHSS1HIDS79QecQboP1Kyrgd0uxakWvd+XeZN5d7pSMkXpv27F606rNVb17j0i4o8B82ms510UrG4s3yLEF3IoTpkqpOXaQcnzP5h+aXthOge4x1jWYmVuzVhhqxKDAurLCu1hY8MSm36FphbbPW+9kQHb4xj3Yavfk8BQW2BUu4QkWyinW46d/4p6TJCqxwUcaGAfO5bZ2ModILd0D0IYEVP4By+KdSI58jeefASvwqllz+0bs3Fbxo2jPHOnYvVXlXfdi9JwPsEQ0loHFRyOER5bpEgoaZOjycaTOCfYG6/Etvjm1ewcNl+zkJ1mWwvVijzHvjHtusbwGk/kP5ZKHO8RBWMPBC4Vj9zPo4yK4JJP4W52GlfSv2l/RPoURc5UspLnr0kJtNrwuoXbPoyvEcKvRe8GpZXPiQMupdTJwbHlPsB0kJCazNKVpFhFGkwtAbU9NgEYsjZ927t6ans1LL72TeS+gro4PEXv5LxE91bVxQO3rb+WH3A/fGtNTZO6b6wJ132IXN9oLcubYZnP2PPG7d2rWA0Ge/1Ag/5q8/wLMB399Geb4RPgenE/Hxdu9j7pf+s//BlBLBwjEy+o+ywUAAIYQAABQSwECFAAUAAgICACaWnk/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAJpaeT/Ey+o+ywUAAIYQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAYgYAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Repetition inför provet
onsdag
Några lösningar till uppgifter vi gjorde på sista lektionen.
Khan Academy
Veckodiagnos 10
Detta är en lösning till uppgift 4 på veckodiagnos 10.
<ggb_applet width="1366" height="611" version="4.0" ggbBase64="UEsDBBQACAgIAMitfT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAMitfT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjbjts2EH1Ov4LQUwvENklJlBR4U6wXTRNgkxZ1WhR9KWiJa7Mri6oo+ZKm/94hKcmyvd1sLm2DAnEokcO5HJ4Zjnb69W6do42otFTFhUfG2EOiSFUmi+WF19Q3o9j7+ukX06VQS7GoOLpR1ZrXF15gJGV24VEWcf8mYaOYB2wURFyMYsHCUcgFCxZYUIGZh9BOyyeFesXXQpc8FfN0Jdb8WqW8toZXdV0+mUy22+24MzVW1XKyXC7GO515CNws9IXXPjwBdUebtr4VpxiTyc8vr536kSx0zYtUeMiE0MinXzyabmWRqS3ayqxeQcB+FHhoJeRyBUFFAbg6MVIlIFKKtJYboWHv4NUGXa9Lz4rxwqw/ck8o7+PxUCY3MhPVhYfHhIWJH8csYDSOKU7AiKqkKOpWmDijZ0rIkRbGfEwjFrIgigI/JncrmU46n6YbKbbOOfNk/QahjdRykQuIoWoAGFncVHAoF94NzzW863qfiwWv+omBO499WJdvQDghoMkhCfMYPzY/Br8A4y6Y3igAXCuVW6UYvX2LKKYYPTYDcQOFgTG3hN0c9t1A3RC4IXQygdseONHAyQROJvA/LkbSxUhJ9PAY6ccY7WGlND43ScO7TRI2sNnq7I06H+4LtLNJQnywCabsP/s7s+jT97Do3j/OIAv+lRCnky5Vpi1RkV4Z2fYka7HWhrp+gsLEMJCgEGjKIiBciEgCQ0QREBOREAUhvJIYMTNGyI9gIUA+ipGRIz6yPA1j+C+IrDKGQlBmZiNID0TAUIBCHxFL7wABqZFNEUgX6oNEGKIQNhnzhBoVPkMBgzc/RgH4aLIjIiDow0Z4B/MU+QT5ZjOJEGWIGX0kMFnHYuM6qKSIYcSIUQgJBsnlEgvkY+SbaLriKIuyqY8gStdZ91irsj8LkIZ6dKidrj4dldZH05wvRA7XzdycJEIbnpuMsIZuVFGj7hCpm1tWvFzJVM9FXcMujX7jG37Na7F7BtK6s21lU1Xo7ytVX6m8WRcaoVTluPdZ5WTwTHuv4cUfLATDhXCwwAbP0Z12FaygRguwryrdifMse2EkDqUBkPyuyPezSvDbUsnjMKYTe3NNRZPmMpO8+AnIaqwYXFB3kdmK3N1jcN10jqgqm+81MBjtfhGVMjj645BillDmx9jHAZScvVsKfTYmMYZbCpZoRENwLeUm9/DYD1lCEpwkLIoYoZCY++FaHCVJjKF4ByzCrXGx6c+I70Qf/rIyqd2Gbl5e6JnKD1MWgCte1k1lmxCojpUJ67JY5sKSxKY23PDp7ULt5o4dvtP1el8al5wDi6UFHkFxoCEEA8rgfvDQwr1bGeNZL4WtDLYSuKObzPp1klArYceFG60U8Ne51kZKujAJ7sxIbUsa9o4Sx5LftAtNIevr7qWW6e0hUiP/qlkvxIFCpdLSJNAlqG3njs2Qf9DMdHJCxakugbmZXglR30lOe5WekRM23VyJPJ8PRSN8kKQtulrkpl6oAqHVPK1UnlscN4Pn1Ga4faxM2C3sOd+rxpQQiO0ZdK5NzmeDu8JMf2vPqb1M4P250zo73GFm9qc7Z2dgS4vqe+i48iOlruA8B1DE0YYfQL+dRH0xyHO1nUM9lDz/JpO1Onhnl17DhfRalv2RiN8bWP0BBlmJ7KhMnJ3C9FZU4FlbkSATG9VoV2AHxSoD22t4dQst5Nwk249AFjebiWUlOo7ltj13dLereFhszqatqmeVWr8oNq8hk08cmE46L6c6rWRpCgZawC1+ewgP2mDNoQk4iteUUMDEEaOWtaExgNbUK4Mh1BABV8MS9sLdACumguZiDQ0zqm2RKJq1qGTaJ8clsS09eNe0AdAEj9sgzOEhtfgNeHjoNNy+AZQg8De1BA6zXHH7MdAzE1gwxMmqe6my1jjp0IPDsSFCES9dopZCuBSv22qHSlBni+XAGd7sZC55tXf6BtnrYHgnILMzQAgm4f8ckR0kkTYfwz0tIOd2YObLS/IYzchXnQ17TbkW5xjGdqHffgbWUUk+1O4hVKbxXbph4YYeLfxAtIZJqdGuYzPa98eI3rgPfleMjde2Eg8bMDd7ktL343Ut4ZubtKD9cfnnXRDlIOOdbLgfpnspRfApqUbkfXE63OA1dJe38Amt7VddTyjz8FxmmSh6Jj4MsxE5BS1V6zUvMlTY75gXUKkqDSF7h96aQ5e6M7cuRARN6t4+uuibuhOYOb2ttnfwcPbZ8LBj4Qh/Ig4ew3kNB3mC5MyheHmGIL8fQcOJHiD+MQw9L3ofDN+oy959n9Jvhgo/gMfi98Jt0a4ZlOsyl6ms778ujtBZ/KfofPiVcE5L0iI6IjQJPyWqUBDvRPVh1YA7Di/OOHz1PlXg6rOpAn4UhmGPuU+CgPZ30qDL+CQlYZ6r8rQm8PNi8Cu5H8rT/shsOGmQ4NP6ju7oARCT0LcYh+SD26OzT9GHUnUI3GTYVdu/PbR/jX/6F1BLBwiiMtzSPwcAACoYAABQSwECFAAUAAgICADIrX0/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAMitfT+iMtzSPwcAACoYAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA1gcAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Prov kapitel fyra samt mindre delar av 3 och 5
fredag
Provgränser
- Betyg E krävs 12 poäng
- Betyg C krävs dessutom 6 C-poäng
- Betyg A krävs 11 C-poäng och 3 A-poäng
5.4 Hur ofta inträffar en händelse?
Relativ frekvens
Sid 262-264
Intro från: GGBtube. DubFet textbelklicka för att se hela simuleringen.
<ggb_applet width="379" height="232" version="4.0" ggbBase64="UEsDBBQACAgIAKOAeT8AAAAAAAAAAAAAAAApAAAAY2IzNjFmNWMzZjgxMmExMTUzZTc1ZTY4MDNkYjUxZWRcbWFpbi5naWbtlvk/E44fx6d8ShijiOWbctTImSNHxJD7Jkch5MgIDR8a5ZhcQx8t51DJnCPH5mrCNEZG9nH3mdJyX2FjOfb1/RO+v3+ej9f7+frp9fs7zc7GFMgL5gUAAEBzM2OH43Y+PlOek8c21NjfAwBOAuysnEw4HI7cpcuqKqpQLW0LQ1ULQ6iDNdTB3sLdHup+bA8LX7fjOMC8HWB+7vCH7r5+vvCQ48AQ4b6IcBgyDo5MRKAS4ahjpyMwiXDMcwQ6C4nOOQ4KU4gpT0eW56LwuUh8IRqHxeCrMeWNOGJ1OZGAwzfiiZ1EcgmKikVT6zD0OgyVgCN3EqmdeDoBN95HpJPwGyQ8pw9PHabSaWQ6jTo+Q6fP0jcGyRszZM4wmTNB5cxQd3/QFxYWNrY3dnd3Af/yL/8Pl4SYTsfFFeFg4wgwmJ/0BwB4ssyNDZ2ip4fy3UIvUIT6arLbUtAQ9gv+vv4rrloG8cElTaFStwjvUgCsvvcXG9OIDcYOmBrEbwsmvzlFWDbrEM0FSWV8zh6LPKhpP8Pf6U9wT5hnIEs2Ol7x+2vy/XHO4G7R2k+BcpvBV5kn37++52H6smyh7WRVgFdwVgv4wMXQeUr9PwHD8ZT3Yy4yJ1+MwPGRmer2YJOuHxmSx6MZBe9vACQn6T6wThTkAOtxWWIL2g/PKxlYFnO8vg2KA+/dRb5ll1NslTtLdWoelaHeJDQbReWN76Vsi3HGb4z9KjJ1JaSw+4atc6Wc8g2+FkAVwnIjbr1YTP79c7mjkrZ1BWPcOnp7y2A2rk7hDarMSJ1rXXQ91IVU1fQS9lfAkcBVjZ/++8ndT3hSxw83wojI065HVgmeGTJJ+qxq4RbzRoFEWNFOp8dZN16x28WiLfYXm/R3spprNI9IhbKWT5S/CgQ6uZBuhmnWb6F2nweFBBNVcFYK4dEikWKgRlnd6pXNDZf9kOIxeE5fs5rTHjf+Ms3uYKFft1tj0bZGvC2vpGethbmKTXWki0ufE5twVwlZwRFyO/wf5YB4Zu2qyiJ9n7K3KwKqmmicUykf9m8HBqA18dmEGxUiIWUrwluAxcLl9wb5ckU6B4Njan+7hReHDelWBkzfdqvCN/HmpSdLnh5IpuROL1nPPJZm7O+WllS6oitGv03HSPReytTMtAXXxvo5g257gy72+AgFcPfQG6gB9cTnDXVztAOf8yIFJ6QivDJwMvoGQ0YPcyD2qD6xXaHs/uT61hjkOkNPkwCdNkHclLeIjJ3OUGJH/WoxR7pdBvoTubMs/PjWFrX4TXdf7azeYcWIfN+uVLVGeNh4gppqy1oo7KTPhZ4ZRh+G27iNR9qrW7lsgoX9Uigt1cYk4UwN5EBlk8JoW3CwfPbkllcFLUMj8hTVPKx0jW9epK0pqUfrrpPUzacF9/T5F9luwWkTZB7rT2PXTzW84O9PKCbNWAv0NrqpW3Mp//KoiAG7C2bll5VRfv5gdPympc+VwSAGlS653npnsXfODdY2DYJKPvZP9RvBoMZXD1wLFfX6a4Jcit/VYjGhrwHSSrhsIb61xoQSHarPTtuzgifFyDtbID4I5XOe1592ygKB8fSMloelowQ+PeD0E+u1m2UfYqCRS3PnChitb9EjZsse0DeOOwaxedAl9yvaE8wIo7VOLIR9GIcdEq4bUOfdjGtICqpJ/WvvqWeUx2cDiYQImPynesWzPTuwx/K2Bi5uky7DO6rOVxid5fcttBbpDfEduNO1r+hcK/v8tob1gWDt5Os82brbn1XM1vPsZOfwb+0SmTR7aWjXH5Pmznmd1PsJGpqb110tRfU0RZ7RJ2o71DQ2se26Xo9QzNEfzZzP92PxPUfKISEPInby5c9peq4qnqo/0vPVG/nKPNEelXxXQjcbdzlHqqnahCI19UM+X9Gsb6RVrEvhRjK4nthdSWrw/+GCkTio5i09AtU+ssChTSq1taa+A2ZwDnx5MnZi6PHU+jFwjI92+aHC3M/TPlG1ou773M6VBQRV66LO9q8mnzxTKWtk8+vPoedfBLWQ3edzrW3/kFN9kNhr6q+UGa5aXvfwAe1UhWSphBiqWz0ilj9zABIcAOpj5ISWLbPzJz/hdxGTeODZA/QtIG5uZN/ScqkjegKepjYOrkHIp9nZ+8QKYeTsK9xm/Nb2ZGa1dwaU1pufEZwH1fHEPe3VRf3SPaxceuchrDb2vXQoTIUudMTs2bS3CpooX/7QbD9647GVpql4+QXBF7kyqjZy44aBbx1XFRlzS23UujWmW3THiRKVpwsWEmcnQs2QF39BUZvPU2zF2zS4UtxW2zyz8+A3dJZe05O+DCDCm6sUwUYhvj1QC5YgU9W+dc/B2y/u8B8U/QmkGr6aVNuNncq1cKwsip60SZBAn2D6vXFiI16y7Dj3UCQBSOGjq7or+7rqXXvx1kMxZN5yKAK+fVfoo+/e/VVLWkBK199S53eO2lnAgZmVLRHl5dzpMfnoIQCzqNayOZf3Z2g7E7B0S5PESpf0khwlEJSKGa7oCwiDORVRn/rf4yrowAOI3WNlFmmnMudLNfsUb/unTryHkr/yL9lv0pPfXmN37640xchrp7WzxmCW+CDTSR8SX6ecqCmKBNRgxZMnffIlJbofiTu2rJ/BQtQCmYthM3wHYStoOD4kwhlPM/yb7CBa9tbJ+XxWdW8waFVrak/kTY/8jFmmmgr3AFBHrdWbG4HrXsL6iPfLWtBw5uTzenj1O4E0nyoIKUfi2jvx+QSldeGKU2NOB9fWWa+kYwhZ40BhjwlBmswFv964tmJP/oTR/sQBoUTptMTamRv76RuV9Q86Lva4fl0auCXqk4rrEcRqgdts4H2QWgKwaehAZ0DSSljVjV9FFNcztivf8fg0jwg+WnuKsVJG49Fx499USKuxF1TxYqZO38m4ovM7LHQg+pIkJTCc4PUgK3U2DQTlPROieEBe/fRFbX/SduP8fL3L/nuXjUzgSJ2zuVw67loRqYUTa/N6seayvhkqCrws3xdeQe61pjMzS/Tx7Yww9kpwPMxwLN9BtLkqnbEQWVZhW22qUzixzzvBG+ENAl1zt69KKv1zAygp0a5whQ1na8Dx6QVf3L9jY/w8Px5qMRhnGpbUTifSwPld1GruZuuHsx+OVFZvwqYV+iFXFzqy/fRrgmV46wcq77CGOga7Kx4EbBdaR2Gmvs+tBQllv9bsPUProsQt0vX1cHkgv18tLOo930tnP/5jA2l+dUIiykb54wZms/ahu7JuHIx1wXOWHsanT2S38Kfmmp+zyVL6yLFyDLyV9FIooikaPbKeD6B2osuBAlkxEWzfinbHBBZl3fjbRd9phX+ih61Yz54dClY1wGQ9we6r/3tXzE1sjOug9xP/C1BLBwhg3Rzv4AkAAOALAABQSwMEFAAICAgAo4B5PwAAAAAAAAAAAAAAACkAAAA4NjhjNWUxMWM0ZGNjNzkyYTE4YmU3NmQ1ZThmMTUwYVxsb2dvLmdpZiWUezzT+x/Hvy7TcmtpZVFKym2WNMevhWLut8UMNXeOS2eicreT6xAtSSuXJtfJbS5poZ1x/GKSrFxaUobEji7GUX3r4Hx/8/g9P6/36/N+vN//fj6vPHeCg4qihiIAACpOjrZE6Y2WliFcTur7Z4g+ACAHuLuS7Hg8HgyOUNMy0D6oZ6F5CH7I7YDhKSOMqYmJJQaHx1mc1rEgHrUm4fDOOAcSHk+wdyXKYii7zKNV7dMUThdibChY4gUdQpalS+o+7yKd8JJfAjOxYQx7MsUhONEuuNAqtoSiivztkFmJKvK6zgmiKZno4x+L8yzGepIJiT7+YeTQCO+w+Fx02DWbmNAISuKFi2TsVT/SdWJcTmgM7aJZzpXg7FgqjUpN88kopVxhpNJy0q4W0ugM+haMQgZDzr5JntCrHNSxPWRY1kcECxbBIj+oxM8BEetwCginQPBYEEFdg8dCKkkQggYdPttkQHmwL7ETQ+3SihHoZwv2pC8ezp13JnTbUVusae22eQMUPDMkvCosn03Nr0fRwX0MEF30l0nlmnWpwKZq3rJ2zZm9hqJDKAakzYCOlEAGTMiECZndh/Bs6GxZe8LtthxGRc6dRgaDWcJkFjLZpTUtxIphYt1CcP1g5v1+cvci6QEUOLBOG55hAwAHjuABwJg8XARIhRADgBiAs1F4HspAiNAe2G0qhiNECJQQYfAesU8CABIALoEjJAipUBKUNggAIAAH4XAQgQARKBCFggAAgsMhBAJCodjaJn+ij/INDF6i0e0Ycrut67CZxaStrVhbW2JgAGlrr5uYgDgchMOJ8XgIj2cRA1rP+HCDzrPS0qa8vcVE0nBY2GhsnIRIBInEdTIZCg1dolLXKRQoNhai0Vh0OquQwWKxOMwKFovNZknPFiw2h835PzyO9J1tuUBAp4vodAGHI2lo4EuHPD6Pz+fzBCCdvnHzJshkQkwmyGJBbDbE4UC8raWQz4f4fA5fwBdsIRQIQIEAkjZCISgUQkIhTygSCkUCoVgo2gISiYQisUgkFktdvIVELAbFYkjaSCSgRAJJHQQhqSDIszKlRvolZOKIBE/AanEyHABgOk621qSkqXISJQrphTyVGLAezuVGDydMLde4ufjejNgp3/zjKu3HwdEDuroWyDHbTbme3fJp6Vawfv1MPOlgUf4hBXS1u2ODSuYeX0UMcWrMZzKa68I1N+d2YGN52Lf4axt/h9+iiu/F9K6Xr5VTd74zybwQM4IHfrS2Hh9JpL388QL7whML6NfiNzNVP75ejUx5frLab4lya8NIhaFy+/Kd//p4e8f0mJv5JR/s9VhxgJzgm24Xa2R+TqfRVGO6lRLc/607OYFxy1SVONzQ0nhK5NqMChYLkipXT08KtrkmhwQGCxY0m8X9qwl9+oMTAa2BS3FuXFjd2HjFmqIOR51eUIkdJ6Uv/J4ww5ppvM723a+0WYcT89e8i481eyYkjGDKi4zPbrrlqfskP+8SCOfNyH/oaQ4GZX2zqC/hjoY/G7Gij7Sk4CMKRpB3fKlRg62uLDW/FyiRNUsbZWB8p9+vjHVw+31dI8PI6fg2Fg7b4JqbtCiw7Gzb5dVdEzXFFXmLFJVhzRZNNPuHnWFPnLLmTeRsn1Q9Hn0X4FKvPnoOLLjggRV+V5s6wKip1/06cKQ98La1Suve1R9j27LyTlopl4Va36vNU2DI6+VLPNKHe96T37xBWd/Q21HbPpwy0ds+R03haBbqZTwnqQ2kBkkGrNBfX3o1Be1kRgbDzu9SmI0b6q63zN3BCWv8kJSe2mAd9tPQyvSqud3ykHUcg6j6KeXFIIKC+mfSS6Fasb3ixrdxXo/hvfi1NwVGMx3H7Ew11TH81/Gf89ePrakNjIk9bjULj2Le31rwSla+WLn5Z/guEzNZx+myHGRYG2F4qbv02dWgSlUFLa26MmIrvsB5Zxr+oQ5d5hrq1KvL6NLfzZrw6DzOmODX9IbncLX/TB1VK560vGsn+xH9xt7U/WNm1cNk3yxxmob7q69zS30Zl8JwasAT8WP1uTLnKxXt5tkPMk4O6x/BOx7qwPmhNXTca5M/P/rKTHFXejZa1mesfnv70h4nu2suC4myyG1Rq4l73J9RnKJLyi9d70dqCBPe5758/JlR63H/ezShv+H6hpJWWwd8+EGdtffeI7DZoi5Q7+3iAZOsyr/6v9+vWOkKT/6uFoFGZuvralxWidzfTpn2I6c2fvxYJL+7Qp/yx5B2dkWIwRVfAqCq+yUlmkv2NBrqQ8JgNsZN6YpFBLqJ6qvxo+Y/Qy72LL+NSvMsMpJXdiVF+Zw40Xb+Ybjzxr3xAbrMpPfdxlBz8fPAVpheEWpWP12/7uYDI/+NZlaG3tDhiZGTws7J/siGKEZwoaau86PeYn7j2SHsGUXApZ/qsDyw0SN/03QIKdeBV0s40fUwAJFb8I6+11Fm5W9xXMdTTPSOb0XZNz4vtKRmVenSk4x2QJEp40KLwpCuIazD8mIu5cmlwgJOcWn9THHZ+YVvyWXxRLfYmeUv/o/OEF58KFz/tDNgZbP6lyEsLPj83tJp1fLXbeFKGA6SNPfJH7j3NobxiP5F/YigXMWZcNufyjj3qXO9azI1YLfj/OXOdnt/kRp7cfbps+O/fbO3kHDdGTPc6rtylFkz7/mqQp3qmF/r1tVtVv6dWHa7QcMCx8fig+3bpTnw6kx+34IqT8+4uVcBPeGVUJQWpOz9+ve6nmuOtwwv7Db+RPhqjB30ULgku/ozMQgzq1kQ6o4oZoGHB8/1NTowPQd7X5UVfAaW7MCWaou7qdn2Mt3j08dyihMyFlPm8lCuK1ohZZ7pHv/AOMdOnd6oWDXeJlEC1TRm86XZCTjZEWxb8EGZ/wNQSwcIqAfJRXEIAAB1CAAAUEsDBBQACAgIAKOAeT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAKOAeT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3ZkqPMlb7+/RSELiY8dktNroCnyo5aet+7qqsn2nZ0IAmp6JJADaiWDr+An8Jz67t5hvGb+EkmkySRWIRAK6j/+hcEJJDnO+fkWXI7+tP9eKTcWp5vu85xC3TUlmI5PbdvO8Pj1jQYtPXWn/74m6Oh5Q6trmcqA9cbm8FxC/OSdv+4peMe7WnWoK1Ci7Yxht12t9frtS1d63ex1u0ZA62lKPe+/QfHfWuOLX9i9qyL3rU1Nl+7PTMIP3wdBJM/PH58d3fXkZ/quN7w8XDY7dz7/ZbCqun4x63oxx/Y6xIP3aGwOFRV8Pi/37wWr2/bjh+YTs9qKZyEqf3H3/xydGc7ffdOubP7wfVxC+mscteWPbxmNCGNtJTHvNCEATKxeoF9a/ns0bnTkOZgPGmFxUyH3/9F/FJGMTktpW/f2n3LO26pHQKoZhCdEoqQqmGjpbiebTlBVBZE33ws33Z0a1t34rX8V/hF3FIC1x11Tf5G5W9/U6AKVeURPwBxgOxAqbilimsqEgcoDlgciCiDxeNYFMWiDBZlMGopt7Zvd0fWcWtgjnyGoO0MPMa9+NwPHkZWWJ/owox68IjR5Ns/WGH2vZYiIGcVf6Q+wmr4n6B5jkAw98XAm1b8oPwc0oxyn4NrEYgWkgcXkUcLPijoLUMfIHPfI+qj8N/wv8wXURGJ6S+K8/U+SPFOSDx6LNXjKNIIxb/mZSOpCayxz3UEGQoxuKgDhTB9oBqTbKIAgx00qDANUABRMGGnQFcoP2oK0tgNrCBFV3g5gJRQIYjO/oe18GVUIexl/KrG9FAB7ENYIUgBoR5hhWmPEuoi00uIWAlCFMIe4p8HkL8CUQVTdoZ0BbM6cjXUACuI2IPsnH0eKggoiD8MNAVShfL3AczVm+q86uyVUKGqQgF/IdNkpsVCg1l5XUGcGhrBZTuTaZCAqDfuy5+BO4l5wUqzNmjW0ok2KdEQ/nI0MrvWiNmGC85JRbk1R1wbwg8NXCdQJBOpuDb0zMm13fMvrCBgT/nKN/PWfG0G1v1TVtqX3w7L9lzHf++5wZk7mo4dX1F67kiN6+yOwNxvGNeanaC5G3j+Bpm7Qed+a7nfddkdZepb7Puu58viZr//gpeYNQsMyXfO6OHUs8ybiWsnyTh6HJqZI2vaG9l923SumLDyr3BclNjq8GZKWh2IgKyI6/UvHnwmwcr9F8tz2T2gdiBAiGCDqoSwHy3lQdxi7+gQqCGoGoCZF8Du+D2T6x4kHUo0QyUGAAQRRJkoPCy4h4n4tnUbs8i8t2bUDj2u2nMnL/xTdzS7FAJwZk6CqRd6DKxl9DhZJ85wZIVCEqo2M8e9m657fyGkA4l3XT5M2JkqatAdhsArHq8kI2YYHbviGJbhVYtLqWEZNSyhSnGz+/F9YMCwRHjsimNYismvqFpEKpBkAlV+xvbDJk1tRYojmysu/dy6Tx07eC1PArt3MyOVP/B2Ou5aMxniBc5t4YoIHyv5GbDFzxw9Toni0Y3lOdYoknzG8qk79YUizylF3+rZY3YqbkTAmZypn1idxNW+NfSsqLw5Cn02AWt4V50X6szl8FVPPXf8wrm9ZBKTqQAjw2NSxCrB7YO4HZIZ0iRpOPJ7nj3hcqt0mS25sWaS2bd9k5mi/rxyckVmL+mFrwzsgGPJVL9rdu2RHTwwbZ8G1y6TnXPTsa2R8oZ5aZ7pMfezz9osxgSu2SNrzC4rQSi8znRseXYv5pkZ+oWsttOI3nbMbs4xxe1+Y61pmtOSsF+O2P0FAq6Yo8m1yf3JqLkYmQ+WlwA1fNsbtx99Oirnj7gjqoxtZmXbTKHG5j0zrOx9XZ+1tAFzxRkXnZkrLoQpaqmAqnJHnz1BCeK/Hpg0UP5jYN/Poc1Qs38wcTIT1Mw0LWBW4Ia5t37oegWR4oc/ntv9vuXE1TVjnrOGcCLoVZgN4h+7Ytbd55+LXzBhKIQNz0w2IgYtZVU3zSq1Qw+CUxrSIk5Rdc+cUn6v4M1wq5fmFu7Ag+AWNaReAXXHigVjdhHlMXN/f6dsnG39THsIO+Qg+KaphuQbBvtSM8j4hlbk2/3EY8/w90aon7QUdvG49VvzkdL7T/me0MMT0UGS1dGN+OElPJ2z7fNMhSpewFa1JFvnHQ2fcyY0uZwxvIlQfsx5XGGVuQ8qnjTmr6ZclGKoTiVUvUdKvypUp8ugyhd/KoDih644rA9ViNBDpJVFUKGVoTqTUHUfKW2zKlZnq2G1Bani3kGo7Vy4tiJU53NIVda/8x0L1bvBwLcCDgwQykYq4rhMOUtLXAEoT1ZslOYtTRiErio+RW03yGupE3mJuEGjUYMmfmwZtKeHAdrGMeu547Hp9BUnTGi+d0cPQ9dpzVJspsoFTjEBh1AxIU/aC5Cmgbw/YU8BUcb6CkSpQfgDHbeu2QEft2x2IMetZ+xAj1vPRTWij+ewTlRD8kZ8YKGrwTMvRb5GgutRUrg004EKV2X6Ytn0rSE/i+vBYdtnTZNNWeQAwkjENBi/bBX0re+OeMYXaR57PBnZPTuIxWjE5f2FE1ieb4VJjGzi5sayJjyv9s659EzH59116eRJWagHNYK6DUDHSPwJK6J3dB1oOgaGpqoAEvikzbtaDo4X1/XhBOxQigkikBgsGkIa0RjmRLS1M01IsUs7HFbYtWGFQDvEvaNpFBGqIwOrKiQqETzJ4YTRXE4k/ZRnK/opm4ujzOm9PbJN7yFJQMoLSfwB4SunWKJt3al73gSw2mlcdJHF3IrTm85UydxyKl8FYkIXa3x+aEVACB0/ZDzi4pTVLLYyhHrjsvksEKWzgBpnrHCUr2LtNgRA1xFi7TYHV4hiW+voBtEBVqkOhYCunMgCarVMVlm3frEXfmZ7vZGVcsLPhIMNMt73zVdQ7E33XGdOIm6q+D/s0b4taOMdxFHpfl/599//RwFZ6ZB9nOkMBaiqV6ukFC17aDm3rIau5yvKvRplNR7UyKf9Ia/cMxzbws0FMvUB5irJ2OnZ98qJLH8iS51A/irEXLETFL30BIfv4pfIfL9Y2qjw8Qb2gPGhOudPFnF+UoXvkw1xHWe5riaaBBUfItuB1uF2IsF3cZOzPe62Kcv24lb75mC7hYh07iBCNexvzW2ci3k1SvMKdfBh8IpKXiEV7otX5U1oNvP8Smaebx4po6qZ51f1687ggrWd3ozXcx0/N1WRel0/pDaWhc8g9WYOqW5VpN7UD6nQc9kKUm/n+n0qy9Tb+iC18Z6dbA913EXdX6WLemkf9e6wEh2uGwSrjHe80D0OqrjHwYbcY7Q4KAIEHW5YBCGLuFP+cSgNK/rHGS15MdeeVB6c8GI1HdlY51+2OdnY2IQSKvJikYb0qqUOeut1nYSRYVcEioenAKRDwcK8QDw8bINpgTeLuNqvxtX+xhJCMKftSwxZOdzcgJpmfWgBw7YvHoC7etv3UrZ9beYhtCu7CC/r4yFIB6G9Qw/h5SJFGVZTlOHGFIVmwQ47z4bRMdWZdkCqkucmtGM/Yc00mj02hzNmhGeCYwObvUpISK+LKBiQHhroAJp8upClEYvqKup3CbD6fxmbttMZ2gNREds5NXs3Q8+dMhnLnc3xnkuo4oSTVkJsxVhNzdAg0iilYZcPibp8qG6oFBhq2FVhpML5tTpfi51KUCQtG8q/FGbJnHSWDIYDjVejO3SkN50pU+NOJj4ns1SuDMW5MixHuxvrZcpW72t6Mfjz3Vf4SGE1Auz/f119wPQ5jKzNf3yfusF/BS6ruPjZyhqawLqfG60JNzDITl3VzJQXxnOUnSQDaOpvaQ63Ii0VRXOd4YILOqUrAISXAaT91PCQX+Epgof+Ck8RPNqv8BTBo//s8GTn5SQtsvBNrHI2+bQ+Njk7iSZJl2eNTL4kQznCzmpDWDIEvbC+Ty2+Ok8yCP3ISrjjPzPfjP5VxKO2GCgfDZMP3c50gDqymYQtiVF5mVlntHggn2QAFov+CgHjRgL2p7bnBymoIiJCkJwMJpe2x6O88phEDzQHkzMWbAYvBilU7pV///0fSgTLDIQENqeoGJd0W3uacYRxrAcVGs4SjVp5CmExhbgihRlPNpxGvlcKUTGFpCKFGWcU4X1TiIsppBUpzPiTCOybQlJMoVaRwoxLGI6O2iuFtJhCvSKFGa9uW1Ka42agyM04RcpjxcnLl6ere5aXITAA0jVCDF3VKYB44UDIDdcey9rj0rXPC981TUUIG1CH0KCU5PTVbKX2RNaelK59bnQNqWZgSHTE14YiOQn0rdSeytrT0rXPC36xjiBBRNf5oomY7kpyNFl7rXTt82JToukG1hDVMQQqgWRHtddl7fXStc8NHfciOSfJ0KbrTkeWXy6wOalNYJNDFkiQdcbJmnol6crpPasLXadJup56//qniOJKBtk1Ju3ESJB2WT6dz56sLVWnkqpSDcOpUdD9tOGmoLiFYuFmponK6wY76HzWCUqI5Ed3OiypaCeoviJ5ghNUXdnuyAqCsoThGhNGEoS9NKdOWapIjamiCapOmSErSRStMVFaUgYtr7QAajWmSk9Q9da1vbJU6XWhKhl4PxHXKyU++/1qIXc/s0odrGzyyk7Efrfn8bXhgIukCUqMS2cv1FkggFWCwqE3WBcjcrSOTjBi0Q3UNH4d7WpM2rtFY9KWZLaTI9KsjYxH+8dPOpOXqh1q8GniKqQGpTpIz+/MlZpwTGdWbkS9Nze6d6GADKoIyGBDAvKzjuxtpogMq4jIcEMi8rNOfGmmiHyvIiLfNyQiP+nSAc2UEK+KhHgbkpCFueXDnjvUTAnxq0iIvyEJ+XmnTuxPSHI6Z9bLl59tP19eMONhyfD3JGlyI43gX/8sOQi+NrSll3a1MwmH64xOvy/W6WTU/361qB/AyC2EpFTkv6XJK6nF1ZEGMdAQEsuIISN3STtjK2vulmHMhyqM+XAwjAEdCnWqUt6a8ZUGMc3li74FvlxEK2QmOfNeWMMPGQZ9K2ZQer3Nb6vNpM7bRGplFs1gXrDgbLjoDLugQoyYZoRIi1nrbaCzGxRgqqrhDb3Ba6EmlefjDlYKL2TLkmSm3KBjJ8umX9QcDLhxNMo0Ah9FI3CRaQTG1RqB8fqL7q7sKeQt+Q1VCSKcvS1PoWmD9Ply+30TOzCE8bY86u7l/DIj5+aymfNpSTfz5s7vzi1O+npyE4UYSowLpR3XTNqX+4/jDMc+VfEfP9XAf1zS8AN1uw1/OVSvqqB61QBUYR1Q/VwF1c8NQBXVAdUvVVD90gBUSR1QPVlmCVOr9S23gzVAduu7DJVB9rQasqeNQFavA7Jn1ZA9awSyWw4EyyF7Xg3Z8yYgC0EdkH1SDdknjUC2Ft7W02rIPm0EsnjjSbLsgqRfZU/RlfJ75bfqI4Woyu+UM1R5cdJVEa20QF/J6DiOAFCHUAPx/kIVI5XCba1+/CyG8dN6MD6rFYzqjmF8GcP4OQEjrrxYZK1glJET7Mi5kyCcTUm3tbHvqxjHL+vh+KpWOJJd4/g6xpGFPAkkSeUNBmqFJI2RBAgZGoAG0ClV4Wa6hnN2HIiBPF0XyDe1AlLfMZBvYyDPUkDSytsT1ArIuGuggxOzncG2dPtdjOT5uki+qxOScaSzJSTL7LX8SXS5XInFoV7IXZSffc3Z/ou9IFotZyqK34rCdvgU5isWw2WufXajZTH9PLcjZNP7LFeZZFJ2QFdhN9R0v51QS6KWuBs27oVtVLdUMfS3NenrbhtZj3y+LxDgTnK1joPhgL2Jna83Ot6gHW+s3EmurVO0BFuzQOdNcD1AL5b7tkE6iduoQSwoY1g/C0sZxsncVr6SpvVLrmGNFmm7E4W/ycI3X6EwrT+qG1a0Q8NaaXLeRkzrXU3EvK2nQ9xU+85CYW1uNSzSIDlfMqS0du27bN7bpJNYfQwXbdfeLNBvatO+F8t9GyDY0TQCgEGBBuEBseBHI5z62NdpN8ytL2NcT75Gy1acSvP6RlrM1wsi12iNUDM0qOyBrnxgLKPX0fKOqayRxbuPXstNb96IkTXzWpsaCvtBRrDd2thX5uNkcqaJ8ay0ExkBEcc2yZdfMmK+NjzItOu4k1xpUj8Y0Ee1Ab1Y7pmPwxdbRQSrlBo6oY1K3pSxs2+lnX0n7ey5NJtnC+xstFK1Ix9w5QN9Gcr2VskSk93ZWbXKGhEbMbNObQQ+E0nBZHaSGLhBIl6Mulsb1LWc/p9EO0NYQJsocjBM6DfEw2xsOFUMf6826YT2EiUAWO0Y6tw/DeLBKsMk31cbJvm+EcMkazGF4kM1ZD80Allt+wNQP8bDMJ6khmFoVYdhfKzVMAw5BBV0EhsPULiZZR6ySF7ESD5dF8mLWiGJt4tkmZDliQxZnsoI5EJGIB8XhCzR1jOWTA0Owh/sAV+mBr1VUoN01yFLyUXLNhKyWA3x2w4yMziok9eW1HSUdNp0o5O8eygs8GsTPGYiFNRJbqCjHU7I7tUG9WK5bwMNdWb3+JZGTeJBxmG5jB2W9ymHRa/qsFzWymGZzVPYzaDwTzGQH9YF8lOtgNS2CmQZx++9dPw+SMfvk3T8Lhc4fpp4YCIf+C4fmErHL1jF8dN25/hVXYt0I77fZN+L6/zMvt/32pjAJb3CEBgdMfRH11WkQ61JnWNLhvXXhgdLe4UPZ2RzUBvQl/QKQxV15nY+VbUmRT3LE6pmjjF9Xi2l+nzPrCy74iVekkuFK7ov5UC9qgbqVUNAhXsF9XM1UD83A9RlizRuF9Mv1TD90gxM9yunJ8sHySTX+dpvRrAkpvttUE+rYXraDEyXdfhtF9OzapieNQNTfUOYZhNAfO8Ga9FuFiV37I7eUTscza7vjqaBddHzLMt57fbEMsQcWKxq0XLCtCRGyQ3NWQVxBXBqKGQDl9XXtzx7EOdKfCZP4Yci5x6UgBGIdlQsf18CRpSGUa8AY87ux4cFIyoLI07BCGAFGHP2Wj4QGEWvB9JRSRhJGkZaAcaczZ0PBEYxNRqhsjDSFIxQrQBjznbSBwEjMoSJgTooCaOWhrGKicnZv/qwYERlYdTTMFYxMTkbZh8IjLpweLSMw5N0tK/CfdzKboRwuyzUFtvCzVZBqU3SVGaqgYxXinf8IMV50fC9icxoz/QCy7fNaCNzP2DnYRAjhPPjcmE+/wrzO7nPK/fNni8fHbWXTm40/7et5bqexDiu3cf9pFY4brePOwvk00VAVhfIpzUFcicC+SzGMTXc9rzycNtntcIR7xbH5zGOT9bF8XmtcITbxLHS2JVzOQb5qRyD/GHB2BVdjl2JHuh/ReKBQfgD85ECK8yz1Lc7diV/r103y+dwkYPZNMyEC0IyjFYXM7rKsJYKaaONELKqwLb1jKDOD7xQk7cLx3/We6fE7GzBCimpvbIoM5EWd+jcX9EEzmaxZNAYlhQqTRtyN3nuDxct1NUsFn1vTMNWebZt3RhRxtiHbhS33c9mxj4ad/pkgbE3xAPX8oHhzNhjYeytr6i6sTd+XmN/3TidOHhLMjwUS6KqSUtyMBzirU0zONR4Q7Js9mVTVKU4VAE6SoYqTeJQzg5NMH+fgvPK+xS8qFV+BOw2z/QyxvFsXRxf1glHYOwWx1cxjqfr4viqVjjqu8XxdYzjybo4vq4VjnS3OL6JcfyyHopvaoXijrvX3sYofl4Pxbe1QhHtFsV3MYpX66H4rlYobrUnI4vi+xjFT+uh+L5WKKrbRLFMiuilTBG9kBmfpetuAlU88U0+YcsepL7MEfVWyRGx9/60SaJvvyaJ6hb52o1hSXGSCGjJ7gZ0OFmi/q9ZonowoncoWSKSvE2LVhKoG4vKmPvX0ty/ksb7VJr7k0XmPhowMpJP3Mguoa5cZ9tcydyDn9fcjxpjW34ac3/TmCZsibknyT4hWLQeWLNY1G2c1hyouTcboytLzD1KdgodmrV/K639G2m7vwjL/Tnf0kO5o0ZUeiwD+x9ylbK7VVYpA1veeLnOlt5pXJt18JZ+3BiWLLH0qXGEsEnNVzGLflSZTFYLrTlQS3/XGEYssfSpkeqkSUmwcvM6IuP9ThrvK2G6P+WbeiQndaBWtHlWZOpvZVA/XWVSB9jyVtB1NvWTxnjFP42pdw/F1KcGesKD4dBtYzh04JZ+2hhGFFv61DjP5s6t6bruyDJn5tUN2cMenlqZzyxmWv5YhtXWXHg3GPhWwFlAdbGQDCCFLDMnoYyE1+bWHmM8+Nc/Xc9mp34Gg/yVP4zEyh+XtmcOLcX5v/8V58rvFSdv5Ed2ERBjr2tUzC0VEQoy7AACDBUDzQAG+8NYoAo7SCMY6MgwNH59fjTIYoFJbya24jiXeVrX2kjMdOyxWKbED6wJfwFrBPyJZfX5gzPVm7AXMkVKNTDxEBk5JLi9bKm81YbFnNleb2SlvOkP0pvOdoldL8uAsbbR7s3N/llxWRS5B3ta6Cqutb+g6YNLmj57aDligRefiaoqPqs8qLKdlVfuGUZtYRlBdOkHmKskEwDPvldOZPkTWeoE8tG14bICJyh66wnmRlXcJmJpxNyGmMlQzx4wkCuow8dDUQe8B3X4uFgdvGVRYlIdvFVX5Qx3HJsxYvW9kuusEJAYOQqBt6IQF4eiEFqHmU9EDUygHo5vEuqhdQxqAF0HEEN+me5KWS4WK4tfTVn8lZUlsh2h932o1gMRrUORzhgPCKa6DrWM5uSIBtejrGhsTKsuD0SroLoHM3O5WHOCapoTrLf4cxStHqiVwRRlrYxg+MatzKdD0QfUARhijDRN1/dsYD4VBSdLBuKlg5O11l0O+bLWLrB1VhNiME3QVUoRBkhXDZhRmaRMbNmyXB2KJtE9WJarxSrzvZrKfF9VZTa4f16dtUZDOSGM4PkGjEs6J3oXKcVcVnSmBDtPikbJu9Ip0SiNaU4DlyvW92UZYaZ+wxkR4Zkgf2AzIIX461TvEQuAHu73epoBTaB3LY32iaUPAFHNv4zcodsZ2gNRH9s5NXs3Q8+dOmU3WeCbVyCxEVm459sed2dcvUWaB5lpvuMzssMUPj8fWu7Q6nrmH/8fUEsHCJpHzk52GgAAbjMBAFBLAQIUABQACAgIAKOAeT9g3Rzv4AkAAOALAAApAAAAAAAAAAAAAAAAAAAAAABjYjM2MWY1YzNmODEyYTExNTNlNzVlNjgwM2RiNTFlZFxtYWluLmdpZlBLAQIUABQACAgIAKOAeT+oB8lFcQgAAHUIAAApAAAAAAAAAAAAAAAAADcKAAA4NjhjNWUxMWM0ZGNjNzkyYTE4YmU3NmQ1ZThmMTUwYVxsb2dvLmdpZlBLAQIUABQACAgIAKOAeT/WN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAP8SAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAo4B5P5pHzk52GgAAbjMBAAwAAAAAAAAAAAAAAAAAXBMAAGdlb2dlYnJhLnhtbFBLBQYAAAAABAAEACwBAAAMLgAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Sidorna 261-266
ons
Här är det lämpligt med några laborationer. Kanske olika uppgifter som gruperna får redovisa på nätet.
5.5 Statistik i samhälle och vetenskap
Sidorna 267-275
fre
Här kan man tänka sig att eleverna gör egna undersökningar och redovisar...
Medelvärde och standardavvikelse
<ggb_applet width="1043" height="624" version="3.2" ggbBase64="UEsDBBQACAgIAPVzdT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VvNkto4ED4nT6HyYU8JY8k2P7uQVIDUJlXJZqvI5rA3YQvQYmzWlgkklbdJXmFfYF5sW5INxpphTHYOszEHGyy12vq+brUbtek/365CtGFJyuNoYOGWbSEW+XHAo/nAysTsadd6/uxxf87iOZsmFM3iZEXFwHJaxJLtGX/2+FE/XcQfEQ2VyAfOPg4skWTMQuk6YTRIF4yJcjPNtjzkNNm9m/7FfJEOrBkNU9mhVbyO1pkohP1V8IanxeWVut065GLMNzxgCQpjf2B53bYlv31gieA+DQeWa9uqhQws0naOOqHJkb2LOOGf4khI8YPykE5ZCPAnYhcyhDay19FdMxBGKOWfGFBFZFv/SjHQZ5kf8oDTSMJUUwQhhD7yQCxgOIbZLRifLwCGh7tamx/HSTDZpYKt0PZPlsQg6EgD7PKLnievUpgx3I/gltvFbWK7todtTDoeCOZ9HmmRnuN2MHHcttvpEH0DtpkwIQBKiuiWpQWh84QHe8blxet0GIeHpnXMIzGia5ElygucvEkRMrBgSolE8iKahyxvw2CmBfOX03g70ew4WvX73VoNUfOZzkdxGCcoATQeTH+ef071p5KRE91L2UrGVhK5Dql03497REmoz6n+1DbkkZ5aDhwXqLFd3IanSDZIgsF5C26U8QeWhbKIizfFBXjN8oBUyv+WraawaMp+s1eJ70ll/6riVf3KcjL8zPXIDX5WGgXMZauoAJ6Pwm3vlCDeC3r2KTmylyv872Y556Cvp2EasPpLlkQs1IskAg/O4izVK1H7qFIfMJ+v4FJ35Pek0iv/AKZ1a8DmCSsMpIOL9gvVa5cXYqW5f1VMQs4hBaP4AmIkGE5Io71lAQs311+TgKHYX6BU0CigSUA3G75kOphlAiLMwHp1/W1JI/Tyzfjl5P3rXy0UUAEaZPhkIVsxiClCLZMoW7GE+3uXGcoQ+6gPc8rymbVbhQlkwI1V9Nyv23zUwSOh/5alBIF2vaDwrYWLoLeDUFomRWl7Gwf5nXFBL1CueICwtdYKIMozFuQPD5EveLQGlSp8lCy2j/taZ8nRNQ93M+JUGfGazoh7YaTCiFdlpNt0RtpVRpymM9KpMkKazkj3EkcqjPSqjLhNZwSy5wolvcZTgi9PmyolRtra+FCCjby18U9gbCSuncZTYmSuFy8xUtdLLDFy10teckleDUqM7LXxqRoxstcGhNftOmGpLO4UeF4QuAU0D6yf/s5i8UtpI/Nn3aJ0HHMp2FZYZQ33SppdkzS7DjpyhG5S3ZatjZE8YIzOsQXpVu6Do3V8/TWa1wboPBSAd6xaI3XGdiOXrVtdtpxGtY3t/j+MbfyYbkBqY5haVrtpbuzPQ/wEDQkcDhwuHB4cbTg6cHTh6MGBbXmSkliKYimLpTCW0liKYymP5QAsRxD7i4VMrwnh1tbxPBQ1+3KqWHB/GcF8Vb2vwG5a6Kj0ecpAGFdN9BSf516P+ro6LQuh5WL9oWatm5/iKvV+vFrB4wFFdKUqejRSaLl8+wBRu2BAzzwTRWvpiak15nrudO/yQCNfxd6ZPnw7ksm4Fg7j2XgeGnN4BRNp2Q5uE7fX9pwetm3n3gDq4FcL5BBC31mwhuT2itoZ8aXGyv9O9xsSfC4iI6x+h7t9B6Safjgk5FxAxg7jf/W1e/h9Mb5pUj/6w+skIyODEdxwRsaXfeAqI0a0bUDKd5oRYxe46ZtZY2MTuOnvQY2NPeCmF0/GxhZw0+uw48sOcJUR8/2FJuwlnc7RjIyk6c/fkZGRND1HGxkZSdOfvyMjI2n6L5uRkZE0nhEjI2n8foCRkTSeETMj+fETkuNNwiFNRguaiMpWofQMRHGeoSFKBtZnuPsT5MqTI09tecL7E8lPX3JmDhuML+Rf/PQs6m4x6iFVb73ZNke1jhIVt9kG26S2dd7NZikTaKvG7uBHzUnT1ajT3FFlPH434HdVUUbr628IXIJJt1iuk3jDRM2640N+UeAI6ez6nwQRG8GQDUvqVlUfLLrxTXash2r8cG02Okal1mg9UKOHAuqq/F9CeV38sfrZv1BLBwiqDnAABwYAAIo9AABQSwECFAAUAAgICAD1c3U/qg5wAAcGAACKPQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAEEGAAAAAA==" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" />
Fri att använda. Från GeoGebraInstitutet
Gapminder - övning
www.gapminder.org
samtidigt som vi kör muntliga nationella prov får elevernas uppgifter på gapminder att jobba med.
Film - undertexter
En tanke är att eleverna får en film var från Khan Academy och att de gör en översättning till svenska av den engelska undertexten.
Monty Hall
Lös det teoretiskt eller leta rätt på en lösning på nätet.
Praktiskt experiment för att testa om det stämmer.
Redovisa
http://sv.wikipedia.org/wiki/Monty_Hall-problemet
5.6 Vilseledande statistik
Sidorna 276-277
må
5.7 Några statistiska lägesmått
Sidorna 278-282
ti
Nationellt prov Ma1C - Onsdagen den 14 december
Behovet av repetition gör att vi kan senarelägga avsnitt 5.6 och 5.7
Muntligt Nationellt prov
Egna undersökningar och gruppövningar
- Sannolikheterna bakom "Kasta gris"
- GapMinder