Begreppet gränsvärde: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 1: | Rad 1: | ||
== Teori == | |||
== | |||
{{defruta | '''Gränsväde i en punkt''' | {{defruta | '''Gränsväde i en punkt''' | ||
| Rad 6: | Rad 5: | ||
: <math> \lim_{x \to a} f(x) = b</math> utläses gränsvärdet för <math> f(x)</math> är lika med <math> b</math> då <math> x</math> går mot <math> a</math> | : <math> \lim_{x \to a} f(x) = b</math> utläses gränsvärdet för <math> f(x)</math> är lika med <math> b</math> då <math> x</math> går mot <math> a</math> | ||
}} | }} | ||
=== Beräkning av gränsvärden === | |||
{{Exruta | '''Beräkna gränsvärdet algebraiskt''' | {{Exruta | '''Beräkna gränsvärdet algebraiskt''' | ||
| Rad 30: | Rad 31: | ||
Rita grafen för funktionen <math> f(x) = (1 + \frac{1}{x})^x </math> och uppskatta gränsvärdet för <math> \lim_{x \to \infty} f(x) </math> | Rita grafen för funktionen <math> f(x) = (1 + \frac{1}{x})^x </math> och uppskatta gränsvärdet för <math> \lim_{x \to \infty} f(x) </math> | ||
== Lär mer == | |||
Versionen från 6 september 2018 kl. 11.15
Teori
| Definition |
|---|
Gränsväde i en punkt
|
Beräkning av gränsvärden
| Exempel |
|---|
| Beräkna gränsvärdet algebraiskt
Vad är gränsvärdet för [math]\displaystyle{ \.. \frac{x^2 - 4}{x - 2} }[/math] om [math]\displaystyle{ x }[/math] går mot 2 ?
|
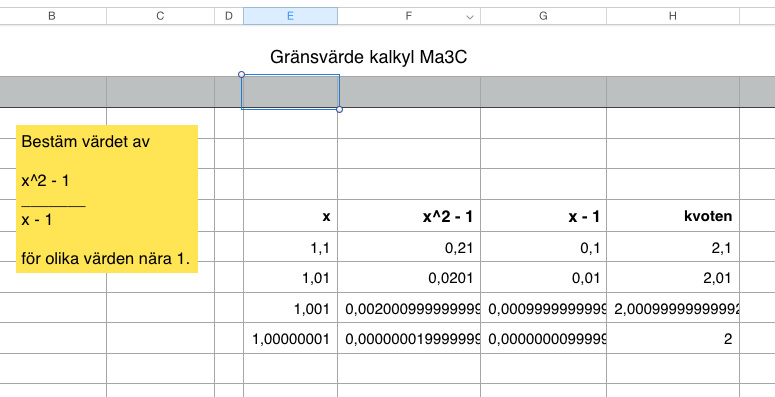
Numerisk beräkning av gränsvärden
Många gånger kan det löna sig att använda ett kalkylprogram om man vill se hur ett uttryck närmar sig gränsvärdet. Här syns ett exempel i Numbers:
Fördjupning
Rita grafen för funktionen [math]\displaystyle{ f(x) = (1 + \frac{1}{x})^x }[/math] och uppskatta gränsvärdet för [math]\displaystyle{ \lim_{x \to \infty} f(x) }[/math]