Normalfördelning: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) (→Övning) |
Hakan (diskussion | bidrag) |
||
| Rad 125: | Rad 125: | ||
{{matteboken |[https://www.matteboken.se/lektioner/matte-2/statistik/normalfordelning Normalförelning] }}<br /> | {{matteboken |[https://www.matteboken.se/lektioner/matte-2/statistik/normalfordelning Normalförelning] }}<br /> | ||
|} | |} | ||
=== Övning === | |||
här kan du läsa om normalfördelningen och testa hur den uppför sig i Geogebra | |||
{{GGB | | |||
[http://www.malinc.se/math/statistics/normal_distrsv.php Malin C - teori om normalfördelning] | |||
}} | |||
{{clear}} | {{clear}} | ||
== Exit ticket == | == Exit ticket == | ||
Versionen från 1 maj 2018 kl. 10.36
Teori
Definition


| Definition |
|---|
| Normalfördelningen
Normalfördelningen har täthetsfunktionen
där μ och σ är normalfördelningens karakteristiska konstanter: μ är väntevärdet och σ är standardavvikelsen för fördelningen. Denna normalfördelning betecknas med [math]\displaystyle{ N(\mu,\sigma)\, }[/math]. |
Normalfördelningens täthetsfunktion kan inte integreras med vanliga endimensionella metoder eftersom den inte har någon primitiv funktion som kan uttryckas analytiskt. Arean under kurvan kan emellertid med andra metoder visas vara 1, vilket den måste vara för att vara en sannolikhetsfördelning.
En standardiserad normalfördelning har μ = 0 och σ = 1.
Filmer
Exempel 1 i boken
Hemuppgift - Normalfördelning

Lös uppgiften till höger.
Är det en normalfördelning och hur vet du det?
Använd datorn till att redovisa ditt svar.
Var beredd att presentera din lösning med projektor.
GeoGebra-förslag till lösning - NP Ma D Normalfödelning
Bedömningsanvisning från NP
Redovisad godtagbar förklaring, t ex integralens värde anger den totala ökningen av antalet bin under 24 veckor
Aktivitet
Normalfördelningen

Gemensam övningsuppgift
Testa dessa data i GGB:
85, 87, 150, 100, 100, 90, 70, 72, 75, 70, 85, 143, 100, 121, 92, 66, 70, 69, 75, 80, 140, 92, 130, 83, 70, 68, 67, 75, 83, 149, 95, 130, 80, 68, 85, 75, 73, 78, 140, 90, 124, 86, 69, 70, 75, 77, 110, 165, 110, 150, 110, 115, 80, 75, 75, 98, 172, 110, 145, 110, 95, 52, 80, 96, 110, 168, 110, 145, 110, 80,80, 75, 89, 95, 170, 110, 145, 120, 89, 72, 79, 75, 95, 220, 100, 149, 100, 110,80, 85, 80, 90, 165, 103, 135, 95, 77, 76, 85, 80, 88, 155, 103, 120, 85, 79, 78, 82, 75, 85, 150, 103, 135, 90, 75, 85, 78, 75, 88, 150, 95, 130, 90, 70, 76, 89, 82, 95, 145, 100, 133, 90, 77, 89, 79, 80, 90, 165, 103, 135, 95, 77, 86, 80, 85, 100, 160, 120, 140, 100, 90, 79, 92, 70, 100, 165, 120, 140, 100, 120, 86, 71, 95, 100, 155, 120, 139, 100, 89, 86, 78, 78, 110, 158, 122, 145, 108, 95, 95, 78
Är de normalfördelade?
Skapa värden i Excel
Övning i att generera egna värden i Excel.
Använd denna fil till att generera slumptal.
Excel genererar två slumptal mellan 1-6. Sedan adderas de. Dessa värden ska du undersöka fördelningen av.
- Plocka in dem i GGB för att göra ett histogram.
- Är de normalfördelade?
Hur många värden behöver du för att det ska se bra ut jämfört med normalförelningskurvan?
Testa även att generera slumptal i GGB.
Normalfördelningskurva i GGB
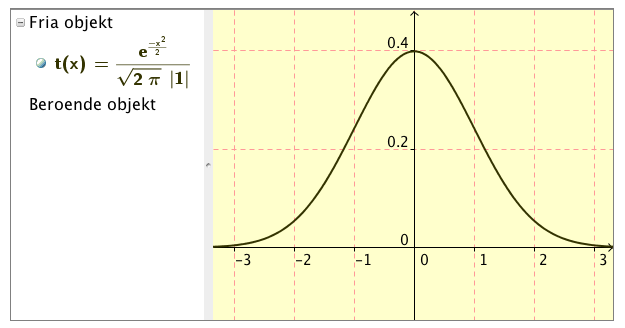
Intressant och lärorik överkursuppgift
Fel vid skapande av miniatyrbild:
Läs artikeln och lär dig hur man skapar svg i gnuplot:
Andelar i respektive kvartil
Mellan medelvärdet och en standardavvikelse ligger 34 % av värdena.
Pascals triangel
Återknyt
e
Lär mer
|
|
Övning
här kan du läsa om normalfördelningen och testa hur den uppför sig i Geogebra


