Grafer

Teori

Begrepp och egenskaper hos andragradsfunktionen

Definition
vertex är kurvans vändpunkt nollställen positivt före x2-termen betyder minimipunkt negativt före x2-termen betyder maximipunkt symmetrilinje genom vertex

Aktivitet

Glad ledsen gubbe och special points

Uppgift

Skriv in funktionen f(x) = a x^2 i GeoGebra. Då skapas en glidare från -5 till 5. Undersök hur grafen förändras för positiva och negativa värden på glidare a. Ändra funktionen f(x) = a x^2 + 2 x -3. Dubbelklicka i fältet just till höger om funktionen i algebrafönstret. Det kommer då upp en blå skylt med frågan Special points. Klicka på den och du ser punkter för vertex, nollställena och där grafen skär y-axeln. Reflektera över punkternas betydelse.

Hur ritar man en parabel om man vet funktionen?

Gör så här

Uppgift

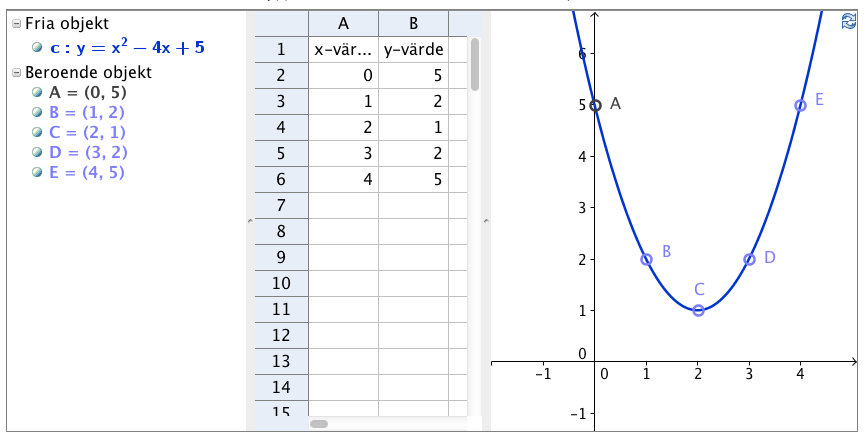
Starta geoGebra Classic Välj Spreadsheet Skriv in x- och y-vären som i figuren nedan. Klicka och dra för att markera alla talpar i värdetabellen. Använd verktyget skapa lista av punkter. Du ser nu fem punkter i grafikfönstret. I algebrafönstrets inmatningsfält skriver du polynom och väljer varianten med lista. Skriv in namnet på din lista, exempelvis L_1. Eventuellt behöver du välja att algebrafönstret ska visa definition och värde. Du ser nu vilken funktion som du ritat till dina punkter. Testa gärna att ändra något y-värde i värdetabellen så att anpassningen blir ett polynom av högre grad.

Man gör en värde tabell. Tag ett lämpligt x-värde och skriv i tabellens x-kolumn. Räkna ut vad y blir genom att sätta in x-värdet i funktion. Skriv y-värdet i dess kolumn. Nu har du det första talparet. Upprepa med ett antal lämpliga x-värden tills du fått minst tre gärna fem talpar. Det är viktigt att du väljer talparen så att du hittar vertex (min- eller maxpunkten).

Om du har funktionen i den allmänna formen y(x) = ax² + bx + c kan det vara bra att kvadratkomplettera.

Många andra Geogebras

Testa dina kunskaper om andragradsfunktioner

Bland annat Jonas Halls GGB med allt man behöver veta om andragradsfunktionens graf. Bör rensas och infogas på denna sida.

Gissa andragradsfunktionen i en tävling

Uppgift
En stor GeoGebraövning' Gissa andragradspolynom

Lär mer

Fördjupning

Det kan vara intressant att som bakgrund titta på denna sida om kägelsnitt.