Nollställe: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) (→Teori) |
||
| Rad 5: | Rad 5: | ||
== Teori == | == Teori == | ||
=== Andragradsekvationer och rötter === | |||
{{exruta|Lös ekvationen: | |||
:<math>x^2-8x+16=0</math> | |||
Vad händer? | |||
Pröva nu ekvationen: | |||
:<math>x^2-8x+17=0</math> | |||
här har vi en ekvation som saknar reella lösningar. | |||
}} | |||
[[Fil:Exempel1_sid_35_Ma2c.PNG|300px|right|CC By --[[Användare:Hakan|hakan]] 3 februari 2012 kl. 17.50 (UTC)]] | |||
{{defruta| | |||
En andragradsekvation kan ha | |||
två reella rötter ''eller'' | |||
en dubbelrot ''eller'' | |||
två komplexa rötter | |||
}} | |||
{{#ev:youtube|LTR1s87IC2I|320|right}} | |||
=== Uppdelning i faktorer med konjugatregeln === | === Uppdelning i faktorer med konjugatregeln === | ||
Versionen från 18 april 2018 kl. 21.32
Teori
Andragradsekvationer och rötter
| Exempel |
|---|
Lös ekvationen:
Vad händer? Pröva nu ekvationen:
här har vi en ekvation som saknar reella lösningar. |
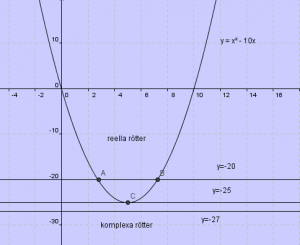
| Definition |
|---|
En andragradsekvation kan ha två reella rötter eller en dubbelrot eller två komplexa rötter |
Uppdelning i faktorer med konjugatregeln
| Uppgift |
|---|
|
Först ska vi repetera konjugatregeln med ett lösblad där det är rad snabba uppgifter. Dessa uppgifter bör klaras av på mindre än tre minuter. |
Uppdelning i faktorer med kvadreringsreglerna
| Uppgift |
|---|
|
Här ska vi också repetera kvadreringsreglerna med ett lösblad. |
En tänkvärd övning i GeoGebra
Aktivitet
| Uppgift |
|---|
| xxx'
|
Lär mer
|
|
|
|
|
|



