Vinklar

Teori

Beräkning av vinklar

Definition
Triangelns vinkelsumma 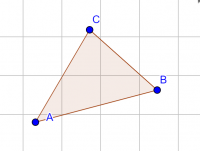Vinkelsumman i en triangel är 180o

Definition
Sidovinklar Sidovinklarna a och b är tillsammans 180o.

Definition
Likabelägna vinklar

Definition
Vertikalvinklar De två vinklarna är vertikalvinklar.

Definition
Alternatvinklar De två vinklarna är alternatvinklar. GeoGebra om Alternatvinklar mm.

Sats

Yttervinkelsatsen Yttervinkel till triangeln. Yttervnkeln är lika stor som summan av de två motstående inre vinklarna. γ = α+ β Bevis: Yttervinkelsatsen Benämn den tredje vinkeln i triangeln [math]\displaystyle{ \delta }[/math]. Då gäller att: [math]\displaystyle{ 180^\circ - \alpha - \beta = \delta = 180^\circ - \gamma }[/math] Således är: [math]\displaystyle{ \alpha + \beta = \gamma }[/math]

Aktivitet

Extrauppgift på kul

Uppgift
Kan du rita en regelbunden hexagon med hjälp av Geogebra? Med hjälp av linjal och passare kan man konstruera en regelbunden hexagon.

Lär mer

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

• Malin Christersson har en fin sajt där jag hittade en Geogebra om yttervinklar.
• På engelska finns en fantastisk GeoGebra Book om Vinklar av Tim Brzezinski med teori och övningar.

Exit ticket

Gör testet nedan: