Räta linjen Ma2c: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 173: | Rad 173: | ||
Avståndet d mellan två punkter i ett koordinatsystem, (x1, y1) och (x2, y2) kan skrivas | Avståndet d mellan två punkter i ett koordinatsystem, (x1, y1) och (x2, y2) kan skrivas | ||
: <math> d = \ | : <math> d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} </math> | ||
}} | }} | ||
Versionen från 9 mars 2018 kl. 16.40
Teori
Repetition och problemlösning
- Lutning på GeoGebra.se
- taxifärd från Geogebrainstitutet
- linjär funktion med glidare från Geogebrainstitutet
Hur ser ekvationen ut för linjen i bilden?
En rät linje går mellan punkterna.
- Vad har linjen för lutning? k-värdet
- Vad betyder et att k är negativt
- Var skär den y-axeln? m-värdet
- Skriv räta linjens ekvation på formen y = kx + m
Beräkna k och m algebraiskt
hur gör man för att ta fram räta linjens ekvation?
Här ska vi lära oss hur man tar fram räta linjens ekvation om man bara har två punkter att utgå ifrån eller om man har en punkt och linjens lutning. Det är alltså så att om man vet två saker om sin linje så kan man ta fram räta linjens ekvation och skriva den på formen y = kx + m.
Det handlar alltså om att hitta värdena för k och m.
| Definition |
|---|
| Att hitta räta linjens ekvation
För att rita en rät linje eller för att skriva dess ekvation behöver du antingen:
|
En punkt på linjen kan vara att veta var den skär en axel, exempelvis y-axeln.
Hitta k
Egentligen kokar det ner till att man behöver hitta k och m. Om man inte redan har fåt k angivet i uppgiften så tar man fram det på det viset vi lärt oss tidigare:
- [math]\displaystyle{ k = \frac {y_2 - y_1}{x_2 - x_1} }[/math]
Hitta m
Om vi har k så är vi halvvägs framme vid att kunna skriva räta linjens ekvation. Det som saknas är ett m-värde.
m-värdet får vi genom att använda en punkt på linjen. Punkten har ju ett värde på x och y som vi sätter in i räta linjens ekvation tillsammans med vårt k-värde.
- [math]\displaystyle{ y = kx + m }[/math]
Då är det ju bara m som är obekant.
| Exempel |
|---|
Bestäm m
Sätter man in värdena så får man:
Vilket ger:
Således: kan vi skriva räta linjens ekvation som
|
Riktningskoefficienten

| Definition |
|---|
| Riktningskoefficienten
|
| Exempel |
|---|
| Bestäm k
Bestäm riktningskoefficienten för den linje som går genom punkterna (1.2) och (4.-3) Vi räknar ut riktningskoefficienten med hjälp av x- och y-värdena ovan:
|
http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-4.png
http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-3.png
| Exempel |
|---|
| Billig städning + uträkning till exemplet
Uppgift Erika anställer en städare och får betala för 4 timmar 450 kr och för 9 timmar 990 kr Erika betalar både grundavgift och en avgift per timme. Hur stor är timpenningen Erika måste betala? Uträkning Tänk så här: Kostnaden ökar med [math]\displaystyle{ 990kr-450kr= 540kr }[/math] Tiden ökar med [math]\displaystyle{ 9-4= 5 timmar }[/math] [math]\displaystyle{ \frac{990-450}{9-4} = \frac{540}{5} = 108 kr/timme }[/math] Avgiften per timme blir[math]\displaystyle{ = 108 kr }[/math] |
Parallella och vinkelräta linjer
Parallella linjer

| Definition |
|---|
|
Två linjer är parallella om de har samma riktningskoefficient.
|
Vinkelräta linjer
| Definition |
|---|
|
Två linjer är vinkelräta om produkten av riktningskoefficienterna är minus ett.
|
Avståndsformeln och mittpunktsformeln
| Definition |
|---|
| Avståndsformeln
Avståndsformeln används för att beräkna avståndet mellan två punkter i ett koordinatsystem. Den bygger på Pythagoras sats. Avståndet d mellan två punkter i ett koordinatsystem, (x1, y1) och (x2, y2) kan skrivas
|

| Definition |
|---|
| Mittpunktsformeln
Mittpunktsformeln är en mattematisk ekvation. Två punkter P1 och P2 som kan ligga precis var som helst i ett kordinatsystem, med hjälp av mittpunktsformeln bestämma punkten mitt emellan Punkt1 och Punkt2 som har benämningen M.
|
| Exempel |
|---|
| Exmepel på problem
Du har två punkter (1, -2) och (-3, 5), hitta mittpunkten av de två punkterna med hjälp av mittpunktsformeln. Lösning
|
Allmän form (linjens ekvation)
Wikipedia skriver om injär_ekvation
En linjär ekvation kan även skrivas på så kallad allmän form:
- [math]\displaystyle{ Ax + By + C = 0\, }[/math]
eller på standardform:
- [math]\displaystyle{ A x +By = C.\, }[/math]
Om man känner till riktningskoefficienten och en punkt (x_0, y_0) på linjen kan man skriva den på enpunktsform:
- [math]\displaystyle{ y-y_0 = k(x-x_0)\, }[/math]
Aktiviteter för flera lektioner
Repetition och problemlösning
Kort repetition
Problemlösning - Diskutera
Jobba själv
Facit: (klicka expandera till höger)
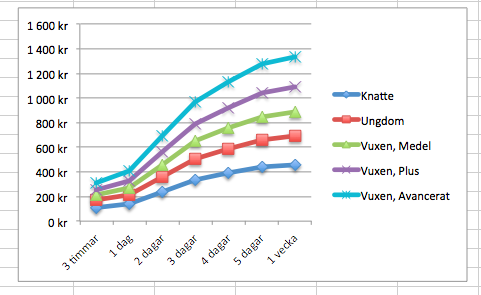
Ser du något som kunde gjorts bättre när det gäller skalan på x-axeln.
Att hitta k och m (algebraiskt)
| Uppgift |
|---|
|
En linje går genom punkterna (-3,4) och (5,-2). Bestäm räta linjens ekvation. Ta nu fram ett eget exempel (med lösning) där man bestämmer räta linjens ekvation när man känner två punkter. Prova att skriv det i Latex på din användarsida i Wikiskola. |
Latex-tips
<math>
\frac{}{}
</math>
Riktningskoefficienten
Parallella och vinkelräta linjer
Avståndsformeln och mittpunktsformeln
Lär mer
|
|
|
|
|
|
- Typtal räta linjens ekvation. Grundläggande begrepp som lutning och m-värde.
- Häfte med enkla uppgifter på y=kx+m som heter Övningsblad räta linjens ekvation. Finns bara på min dator. Jag har delat ut det.
- Två sidor med Blandade svåra uppgifter på räta linjen. Även dessa är från Uppgiftsbanken och (c). Därför finns filen på min dator men kan skrivas ut vid behov.
- MalinC förklarar Räta linjen Här finns det bra förklaringar och en del övningar. jag kan rekommendera fler delar av hemsidan. Sök efter sånt som har med vårt kapitel att göra.
- En laboration om knutar på ett snöre från sid 109 i boken.
- En stencil med två räta linjen där du gör en värdetabell, en graf och en ekvation. Tre representationer alltså.
Repetion och enklare uppgifter
Problemlösning
Klurig läxa
Hitta k och m
Riktningskoefficienten
Parallella och vinkelräta linjer
- Fin sida för dej som satsar på högre betyg på provet än E/D.
- Bevis på engelska om vinkelräta linjer. Observera att amerikaner använder m i stället för k!






