Likformighet och kongruens: Skillnad mellan sidversioner

Versionen från 22 februari 2018 kl. 21.21

Mål för undervisningen xxx

Här undersöker vi xxx.

Teori

Definition

Termen kongruens används för geometriska figurer som har samma storlek och form, men kan vara olika orienterade.

Två geometriska figurer är kongruenta, om och endast om, de kan fås att sammanfalla genom translation, rotation och spegling. Detta kan jämföras med den inom geometrin använda termen likformighet, vilken används om figurer av samma form men inte nödvändigtvis samma storlek. För bevarad likformighet är således även skalning tillåten.

Två plangeometriska figurer som kan fås att sammanfalla genom spegling, rotation och translation
Spegling
Rotation
Translation

Wikipedia skriver om Kongruens_(geometri)

Aktivitet

Uppgift
xxx'

Lär mer

Swayen till detta avsnitt: [https xxx]

läromedel: xxxxx

Läs om xxxxx

Exit ticket

Likformighet och kongruens

Ma2C: Likformighet 71 -74, sidan {{{2}}}

Khan Academy: likformiga trianglar

Likformighet

Alla figurer av samma färg är likformiga.

Definition

Likfromighet är två objekter som har exakt samma form, men är inte lika stora (se bild ⇒⇒).

Två trianglar är likformiga om något av följande är uppfyllt:

VVV: Motsvarande vinklar är lika.
SSS: Förhållandet mellan de tre sidparen är lika
SVS: Förhållandet mellan två sidpar är lika och mellanliggande vinkel är samma

Video

Exempel (Uppgift)

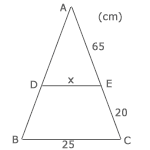
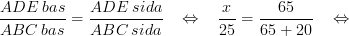
ADE bas/ABC bas betyder att vi tar måtten på sträcken DE från den lilla triangeln och dela den med måtten på sträcken BC från den stora triangeln samt ADE sida/ABC sida betyder att vi tar måtten på sträcken AE från den lilla triangeln och dela den med sträcken AC från den stora triangeln, och det blir alltså summan på AE och EC. Man kan också använda formeln genom att dela den stora triangeln med den lilla istället, och svaret blir detsamma.

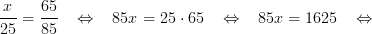
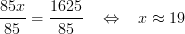
Användningsområden

Man kan tex. använda likformighet i avbildningar när man ska rita kartor och jorden på olika skalor, dvs. 1:2, exempelvis:-

Hund i längdskala 1:1

Hund i längdskala 1:2. Areaskalan är 1:4

Länkar

Likformighet GeoGebra

Topptriangelsatsen

Den här filmen handlar om likformighet och topptriangelsatsen. Observera att sidan som är 15 lång i exemplet gäller sidan på hela den stora triangeln.

Kongruens

Definition

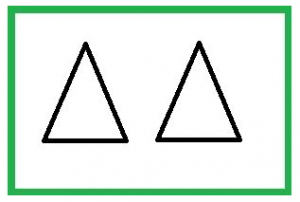
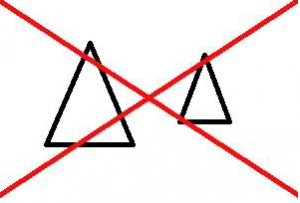
Kongruens

Två figurer är kongruenta om de har samma form och samma storlek.

Två trianglar är kongruenta om något av följande tre fall gäller:

Två sidor och mellanliggande vinkel (SVS = Sida-Vinkel-Sida)
De tre sidorna (SSS = Sida-Sida-Sida)
Två vinklar och mellanliggande sida (VSV = Vinkel-Sida-Vinkel)

Länkar

Bilder