Komplexa tal Ma2c

Teori

Vad ska man ha komplexa tal till?

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

komplexa tal

• Komplexa tal används när man räknar på växelström.
  • j-omegametoden

Komplexa rötter

Andragradsekvationer med ickereella rtöter uppstår när vi behöver ta roten ur ett negativt tal. Då använder vi komplexa tal. Repetera gärna genom att titta på sidan Tal_och_talmängder

Definition
Komplexa tal [math]\displaystyle{ \sqrt{-1} = i }[/math] [math]\displaystyle{ i^2 = -1 }[/math] Ett komplext tal består av en realdel [math]\displaystyle{ a }[/math] och en imaginärdel [math]\displaystyle{ b }[/math]. [math]\displaystyle{ z = a + bi }[/math] [math]\displaystyle{ Re z = a }[/math] [math]\displaystyle{ Im z = b }[/math]

Exempel

x2 = -16 har ingen reell rot men däremot två komplexa. [math]\displaystyle{ x^2 = -16 }[/math] [math]\displaystyle{ x = \pm \sqrt{-16} }[/math] [math]\displaystyle{ x = \pm \sqrt{i^2 * 16} }[/math] [math]\displaystyle{ x = \pm \sqrt{i^2} * \sqrt{16} }[/math] [math]\displaystyle{ x = \pm i * 4 }[/math] [math]\displaystyle{ x_1 = 4i }[/math] [math]\displaystyle{ x_2 = -4i }[/math] x2-4x+13=0 har också två komplexa rötter fast här består varje rot av både en realdel och en imaginärdel. [math]\displaystyle{ x^2 - 4x + 13 = 0 }[/math] [math]\displaystyle{ {{pq-formeln}} }[/math] [math]\displaystyle{ x = -\frac{-4}{2} \pm \sqrt{ (\frac{4}{2})^2 - 13 } }[/math] [math]\displaystyle{ x = 2 \pm \sqrt{4 - 13} }[/math] [math]\displaystyle{ x = 2 \pm \sqrt{-9} }[/math] [math]\displaystyle{ x = 2 \pm \sqrt{9*i^2} }[/math] [math]\displaystyle{ x = 2 \pm 3i }[/math] [math]\displaystyle{ x_1 = 2 +3i }[/math] [math]\displaystyle{ x_2 = 2 - 3i }[/math]

Läs mer: Komplexa tal på wikipedia

Aktivitet

Uppgift

Uppgift
CAS i Geogebra 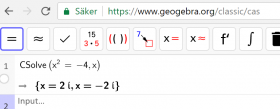Lär dig lösa andragradsekvationer med CAS-modulen i GeoGebra. CAS står för Computer Algebra System. GeoGebra Quickstart Tutorial.

Lär mer

Texter från högskolan

• Komplexa tal i elläran

En wiki med mycket teknik

• j-omegametoden

Fördjupning som hör till Ma4

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Magnus Rönnholm, CC

Konjugatet

Ett komplext tals konjugat kan bildas genom att spegla dess imaginärdel i x-axeln:

Konjugatet till ett komplext tal z = a + b i definieras som

[math]\displaystyle{ \bar{z} = a - b\,\mathrm i }[/math]

För konjugatet gäller

[math]\displaystyle{ \overline{z + w} = \overline{z} + \overline{w} \!\ }[/math]

[math]\displaystyle{ \overline{zw} = \overline{z}\; \overline{w} \!\ }[/math]

[math]\displaystyle{ \left| \overline{z} \right| = \left| z \right| }[/math]

Absolutbeloppet

Absolutbeloppet av ett komplext tal z = a + b i kan i det komplexa talplanet tolkas som avståndet från origo till punkten (a, b) och beräknas som

[math]\displaystyle{ r= \sqrt{a^2 + b^2} }[/math]

eller

[math]\displaystyle{ r= \sqrt{\mathrm{Re}(z)^2 + \mathrm{Im}(z)^2} }[/math]

För absolutbeloppet gäller

[math]\displaystyle{ |z_1 \cdot z_2| = |z_1|\cdot |z_2| }[/math]

[math]\displaystyle{ \left|{z_1 \over z_2} \right | = {|z_1|\over |z_2|} }[/math]