Induktion: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 3: | Rad 3: | ||
! Digital bok !! Pappersbok | ! Digital bok !! Pappersbok | ||
|- | |- | ||
| {{Gleerups| [https://gleerupsportal.se/laromedel/impuls-2/article/9a2b6bc7-6f4d-43ba-b68a-30f98d07a90e Induktion]}} || {{Heureka2| Kap 6 s 102 - 128}} | | {{Gleerups| [https://gleerupsportal.se/laromedel/impuls-2/article/9a2b6bc7-6f4d-43ba-b68a-30f98d07a90e Induktion] [https://gleerupsportal.se/laromedel/impuls-2/article/8882c005-152f-4081-9b2b-90107609c92c Uppgifter Induktion]}} || {{Heureka2| Kap 6 s 102 - 128}} | ||
|} | |} | ||
{{clear}} | {{clear}} | ||
Versionen från 13 november 2017 kl. 14.26
| Digital bok | Pappersbok |
|---|---|
Först kommer en kort sammanfattning av det viktigaste inom induktion.
Sammanfattning Induktion
Induktion behandlas i kapitel 6 i Heureka 2.
Induktion
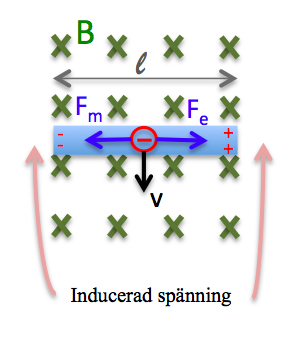
En ledare förflyttas i ett magnetfält. Om man ser till en laddning i ledaren så förflyttas den nedåt i bilden och vi har en laddning med en hastighet i ett magnetfält. Den påverkas således av en vinkelrät kraft. I det här fallet påverkas elektroner av en kraft till vänster i bilden och positiva laddnings påverkas av en kraft till höger. Detta gör att laddningarna förskjuts åt sidorna vilket ger upphov till ett elektriskt fält i ledaren och en elektromotorisk spänning (ems, e).
Om ledaren förflyttas med jämn fart uppstår en balans mellan de elektriska och magnetiska krafterna.
Kraften från det magnetiska fältet.
- [math]\displaystyle{ e = l B v }[/math]
Lenz lag
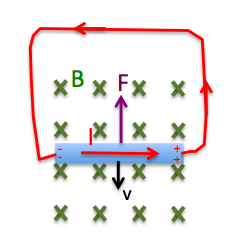
Det finns en kraft som är motriktad kraften som skapar ledarens rörelse. Det måste uträttas ett arbete för att skapa strömmen.
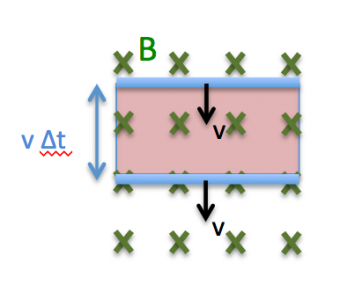
Magnetsikt flöde
B känner vi ju som magnetsk flödestäthet. Det är alltså areaberoende.
magnetskt flöde definieras som
- [math]\displaystyle{ \Phi = B A }[/math]
Där A är arean.
Enheten för magnetiskt flöde är T m2 eller Weber, Wb.
Induktionslagen på annan form
[math]\displaystyle{ e = \frac{\Delta \Phi}{\Delta t} \\ }[/math]
Induktans
En elektrisk ström som flyter genom en krets orsakar ett magnetiskt fält och därmed ett magnetiskt flöde .[math]\displaystyle{ \Phi. }[/math] genom kretsen. Förhållandet mellan det magnetiska flödet och strömstyrkan kallas induktans eller mera korrekt kretsens självinduktans. Vanligtvis används symbolen.[math]\displaystyle{ L. }[/math] för induktans. Den kvantitativa definitionen av induktans är
- [math]\displaystyle{ L= \frac{\Phi}{i}. }[/math]
SI-enheterna för induktans är Weber per ampere, eller Henry (H): 1 H = 1 Wb/A.
Transformatorn

Den vanligaste typen av transformator kan anses bestå av tre delar; primärlindning, sekundärlindning och kärna. En växelström genom primärlindningen ger upphov till ett tidsvarierande magnetiskt fält i kärnan. Kärnan överför det magnetiska fältet till sekundärlindningen i vilken det induceras en spänning.
Antalet lindningsvarv (N) på sekundär- respektive primärlindningen bestämmer förhållandet mellan transformatorns sekundär- och primärspänning:
- [math]\displaystyle{ \frac{U_s}{U_p}=\frac{N_s}{N_p} }[/math]
För strömmarna i respektive lindningar gäller det omvända förhållandet:
- [math]\displaystyle{ \frac{I_s}{I_p}=\frac{N_p}{N_s} }[/math]
Här nedan kommer länkar till sidor om varje avsnitt
Sid 106-112 - Introduktion till induktion samt demonstration
Kap 6 s 113-114 - Virvelströmmar
Kap 6 s 115-117 - Induktans, spole i en krets samt demo fyrkantsvåg
Kap 6 s 118-122 - Växelströmstranformatorn
Kap 6 s 123-128 - Lösningar uppg kap 6 Heureka2
Tekniska tillämpningar
Elektromagnetismen är mycket viktig i tekniska tillämningar, exempelvis elektriska generatorer och motorer.
Om Teslas induktionsmotor som sitter i Teslabilarna.
