Grupparbete Geometri Ma1c: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 85: | Rad 85: | ||
Ni kan redovisa genom att hålla ett tal (med presentationsverktyg), skapa en GeoGebra (med förklarande text och flera steg eller animering) eller skapa en sida på Wikiskola. | Ni kan redovisa genom att hålla ett tal (med presentationsverktyg), skapa en GeoGebra (med förklarande text och flera steg eller animering) eller skapa en sida på Wikiskola. | ||
'''[[Presentationstrick i GeoGebra]]''' handlar om hur du exempelvsi flyttar trianglar och samtidigt roterar dem genom att dra i en glidare. Dessutom hur du på ett magiskt sätt visar eller döljder objekt när du drar i glidaren. | |||
== Lär mer == | == Lär mer == | ||
Versionen från 26 september 2017 kl. 19.03
Pythagoras sats
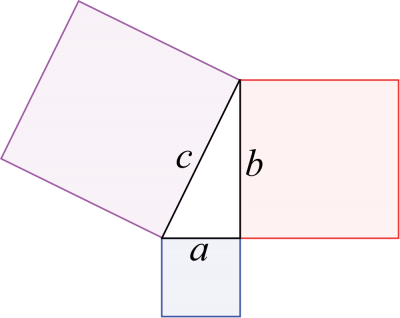
Varför ska man kunna Pythagoras sats?
- Det hör faktiskt till allmänbildningen
- Man kan faktiskt använda det i verkligheten. Tag ett rep och spänn upp en triangel med sidorna tre, fyra och fem meter och du har en rät vinkel med stora mått. Bra om du ska sätta ut en husgrund till exempel.
- Den är oerhört användbar till att lösa matematiska problem.
Definitioner

- En triangel är rätvinklig om en vinkel är rät (90 grader eller pi/2)
- Den längsta sidan i en rätvinklig triangel kallas hypotenusa.
- De två kortare sidorna i en rätvinklig triangel kallas kateter.
Sats
Summan av kateternas kvadrater är lika med kvadraten på hypotenusan.
- [math]\displaystyle{ a^2 + b^2 = c^2 }[/math]
Bevis
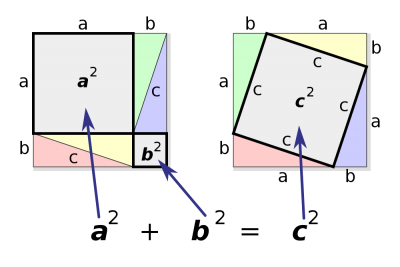

Bilderna kommer från commons.wikimedia.org
Aktivitet
Vi ser en film från TEDEd
Vi ser en film tillsammans på TEDEd.
Kolla om du förstår
Välj gärna ett bevis och fundera på om du förstår och kan förklara för dig själv hur beviset fungerar. Vad bygger beviset på för satser?
Länken nedan går till en s k GeoGebraBook. Det är en samling med flera GeoGebrakonstruktioner som du kan bläddra mellan. Den heter Proofs Without Words, av Steve Phelps, Feb 2, 2015. Tanken med att den är utan ord är att du ska få klura själv.
Proofs Without Words for the Pythagorean Theorem.
Problemlösning
Vi presenterar en serie problem av algebraisk geometrisk karaktär vilka lämpar sig att lösa med hjälp v Pythagoras sats.
Diskussion
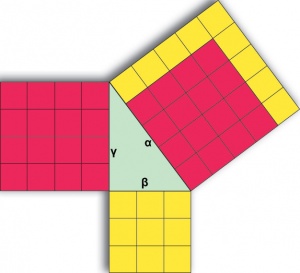
Är beviset till höger ett fullt allmängiltiga bevis?
Vilka grupper?
Tre per grupp, Vi lottar.
Ämnesområden
Välj ett bevis av Pythagoras sats genom att söka på geogebra.org eller Google. Lämpliga sökord: pythagorean theorem
Innehåll i presentationen
Använd text, bild, animeringar, filmer, etc för att skapa en pedagogisk presentation
- Definitioner, satser och bevis
- Exempel
Redovisningsformer
Ni kan redovisa genom att hålla ett tal (med presentationsverktyg), skapa en GeoGebra (med förklarande text och flera steg eller animering) eller skapa en sida på Wikiskola.
Presentationstrick i GeoGebra handlar om hur du exempelvsi flyttar trianglar och samtidigt roterar dem genom att dra i en glidare. Dessutom hur du på ett magiskt sätt visar eller döljder objekt när du drar i glidaren.
Lär mer
Webbmatte om Pythagoras sats Fendt nr 2
Uppgift: Titta själv igenom Geoegebras film om pythagoras sats.
Uppgift: Hitta ditt eget favoritbevis på nätet och visa för oss andra. Bra övning: Upptäck Pythagoras i GeoGebra.
