Grupparbete Geometri Ma1c: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 73: | Rad 73: | ||
Vi presenterar en serie problem av algebraisk geometrisk karaktär vilka lämpar sig att lösa med hjälp v Pythagoras sats. | Vi presenterar en serie problem av algebraisk geometrisk karaktär vilka lämpar sig att lösa med hjälp v Pythagoras sats. | ||
== Elevsidor == | |||
[[Pythagoras grupp 1]] | |||
Versionen från 21 september 2017 kl. 12.28
Pythagoras sats
Varför ska man kunna Pythagoras sats?
- Det hör faktiskt till allmänbildningen
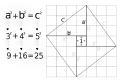
- Man kan faktiskt använda det i verkligheten. Tag ett rep och spänn upp en triangel med sidorna tre, fyra och fem meter och du har en rät vinkel med stora mått. Bra om du ska sätta ut en husgrund till exempel.
- Den är oerhört användbar till att lösa matematiska problem.
Definitioner
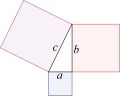
Vi definierar kateter, hypotenusa och rätvinklig triangel.
Sats
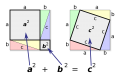
Summan av kateternas kvadrater är lika med kvadraten på hypotenusan.
- [math]\displaystyle{ a^2 + b^2 = c^2 }[/math]
Bevis:
Webbmatte om Pythagoras sats Fendt nr 2
Även här kommer bilderna från commons.wikimedia.org
Uppgift: Titta själv igenom Geoegebras film om pythagoras sats.
Uppgift: Hitta ditt eget favoritbevis på nätet och visa för oss andra. Bra övning: Upptäck Pythagoras i GeoGebra.
Aktivitet
Vi ser en film tillsammans på TEDEd.
Vilka grupper?
Tre per grupp, Vi lottar.
Ämnesområden
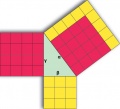
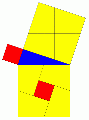
Olika bevis av Pythagoras sats
Innehåll i presentationen
Använd text, bild, animeringar, filmer, etc för att skapa en pedagogisk presentation
- Definitioner, satser och bevis
- Exempel
Redovisningsformer
Ni kan redovisa genom att hålla ett tal (med presentationsverktyg), skapa en GeoGebra (med förklarande text och flera steg eller animering) eller skapa en sida på Wikiskola.
Aktiviteter
Vi presenterar en serie problem av algebraisk geometrisk karaktär vilka lämpar sig att lösa med hjälp v Pythagoras sats.