Sin 3x = cos 2x: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) |
||
| Rad 42: | Rad 42: | ||
Svara på frågorna i formuläret nedan så vet vi vad du kan och vad du kan behöva diskutera mer eller repetera. | Svara på frågorna i formuläret nedan så vet vi vad du kan och vad du kan behöva diskutera mer eller repetera. | ||
{{Lista | | |||
<html> | <html> | ||
<iframe src="https://docs.google.com/forms/d/1LsS_gTbIPWMgaAWcJkw6DFuULON_MQJwtG_Y15snIsE/viewform?embedded=true" width="760" height="500" frameborder="0" marginheight="0" marginwidth="0">Loading...</iframe> | <iframe src="https://docs.google.com/forms/d/1LsS_gTbIPWMgaAWcJkw6DFuULON_MQJwtG_Y15snIsE/viewform?embedded=true" width="760" height="500" frameborder="0" marginheight="0" marginwidth="0">Loading...</iframe> | ||
</html> | </html> | ||
}} | |||
Versionen från 5 september 2016 kl. 20.10
Flippa teorin nedan
Lösning
Denna gång ingen film men du får förbereda dig genom att titta på denna förklaring (förenkling av den i boken).
Vi ska allts lösa ekvationen sin 3x = cos 2x
Repetition: Vi vet sen tidigare att cos x = sin (90°-x)
Alltså kan vi skriva skriva att cos 2x = sin (90°-2x)
Sätt in det i ekvationen ger sin 3x = sin (90-2x)
Den enkla lösningen ges av att
- 3x = 90 - 2x + n 360°
- 5x = 90 + n 360°
- x = 18 + n 72°
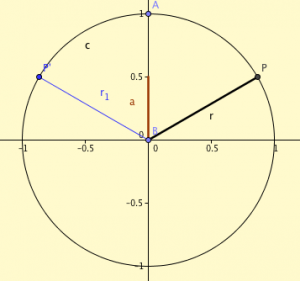
Den andra (inte lika uppenbara) lösningen får vi om tänker på att punkten på enhetscirkel som speglas i y-axeln också är en lösning. Det är alltså 180° minus vinkeln, se figur.
- 3x = 180 - (90 - 2x) + n 360° ( uttrycket inom parentesen är samma som i den enkla lösningen.
- 3x = 180 - 90 + 2x + n 360°
- x = 90 + n 360°
Lösningarna är x = 18, 90, 162, 234, ....
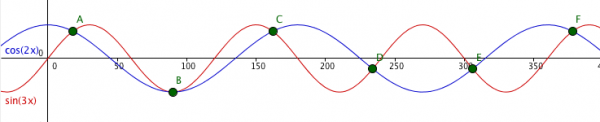
Lösning med grafritande hjälpmedel
Rita de två funktionerna y = sin 3x respektive y = cos 2x och finn skärningspunkterna.
Svara på frågorna nedan
Svara på frågorna i formuläret nedan så vet vi vad du kan och vad du kan behöva diskutera mer eller repetera.
Lista: (klicka expandera till höger)