Sin 3x = cos 2x: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 1: | Rad 1: | ||
[[Category:Matematik]] [[Category:Ma4]] [[Category:Aritmetik, algebra och geometri]] [[Category:Trigonometri]] | |||
== Flippa teorin nedan == | == Flippa teorin nedan == | ||
{{flipped | Denna gång ska du titta på en algebraisk lösning}} | {{flipped | Denna gång ska du titta på en algebraisk lösning}} | ||
Versionen från 1 mars 2016 kl. 19.15
Flippa teorin nedan
Lösning
Denna gång ingen film men du får förbereda dig genom att titta på denna förklaring (förenkling av den i boken).
Vi ska allts lösa ekvationen sin 3x = cos 2x
Repetition: Vi vet sen tidigare att cos x = sin (90°-x)
Alltså kan vi skriva skriva att cos 2x = sin (90°-2x)
Sätt in det i ekvationen ger sin 3x = sin (90-2x)
Den enkla lösningen ges av att
- 3x = 90 - 2x + n 360°
- 5x = 90 + n 360°
- x = 18 + n 72°
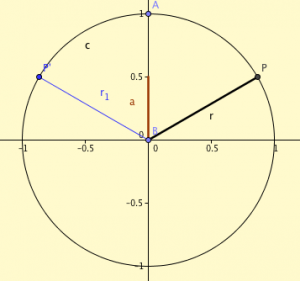
Den andra (inte lika uppenbara) lösningen får vi om tänker på att punkten på enhetscirkel som speglas i y-axeln också är en lösning. Det är alltså 180° minus vinkeln, se figur.
- 3x = 180 - (90 - 2x) + n 360° ( uttrycket inom parentesen är samma som i den enkla lösningen.
- 3x = 180 - 90 + 2x + n 360°
- x = 90 + n 360°
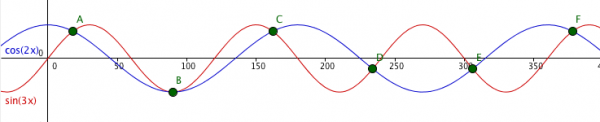
Lösningarna är x = 18, 90, 162, 234, ....
Lösning med grafritande hjälpmedel
Rita de två funktionerna y = sin 3x respektive y = cos 2x och finn skärningspunkterna.
Svara på frågorna nedan
Svara på frågorna i formuläret nedan så vet vi vad du kan och vad du kan behöva diskutera mer eller repetera.
När du gör filmen så får jag underlag att bedöma förmågorna att kommunicera och redovisa lösningar.
Använd till exempel Screencast-O-Matic. Filma och peka på lösningen ovan. Förklara. Lägg filmen på Youtube.
Screencast-O-Matic finns här.