Lektion 9 Cirkelns ekvation

Definition
Cirkeln En cirkel består av de punkter som ligger på samma avstånd till cirkelns mittpunkt. Avståndet från mittpunkten till cirkeln är radien.

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Sid 37-39 - Cirkelns ekvation, av åke Dahllöf

Centrum i origo

En cirkel med radien 2.

En cirkel med centrum i origo och radien r kan skrivas på formen:

[math]\displaystyle{ x^2 + y^2 = r^2.\!\ }[/math]

En punkt på cirkeln har ett avstånd från origo som beskrivs genom Pythagoras. I figuren till höger är radien roten ur 4, dvs 2.

Wikipedia skriver om Pythagoras sats

Flytta cirkelns mittpunkt

En cirkel med radien 2

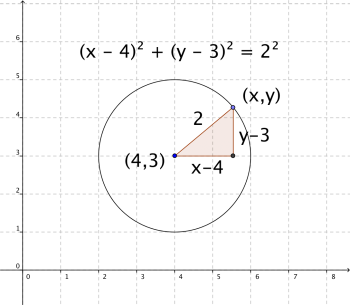
I ett koordinatsystem kan en cirkel med mittpunkt i (a, b) och radien r, beskrivas som mängden av punkter som uppfyller ekvationen

[math]\displaystyle{ \left(x - a \right)^2 + \left( y - b \right)^2=r^2. }[/math]

Ekvationen kan ställas upp genom utnyttjande av Pythagoras sats för avståndet mellan punkterna [math]\displaystyle{ (a,b) }[/math] och [math]\displaystyle{ (x,y) }[/math].

Se det som att man flyttar cirkelns mittpunkt från origo till punkten [math]\displaystyle{ (a,b) }[/math] genom att sätta in a och b i uttrycket ovan.

Exempel

Cirkelns ekvation är:

[math]\displaystyle{ 9=(x+2)^2+(y-3)^2 }[/math]

Den här cirkeln har sin mittpunkt i x = -2 och y = 3. Det är de värdena som ger noll inom respektive parentes.

Pröva att sätta in x = 0 respektive y = 0 ger punkterna där cirkeln skär axlarna.

Var skär cirkeln x-axeln?