Lektion 4 - Enhetscirkeln: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 21: | Rad 21: | ||
:<math>\cos \. (- t) = \cos t</math> | :<math>\cos \. (- t) = \cos t</math> | ||
}} | }} | ||
<html> | |||
<iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/79980/width/1366/height/558/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/auto" width="1366px" height="558px" style="border:0px;"> </iframe> | |||
</html> | |||
=== Trigonometriska ekvationer === | === Trigonometriska ekvationer === | ||
Versionen från 2 september 2015 kl. 23.46
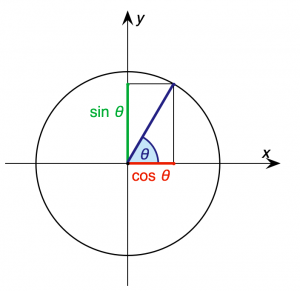
Dagens lektion handlar om trigonometri och cirklar. genom att titta på enhetscirkeln går vi utanför den rätvinkliga triangeln och kan arbeta med vinklar större än 90°. Genom att enhetscirklen har radien ett blir hypotenusan 1.
| Definition |
|---|
Sinus och kosings i enhetscirkeln
|
Texten i ovanstående avsnitt kommer från Wikipedia.se
Viktiga samband
| Definition |
|---|
Speglingar i x-axeln och y-axeln
|
Trigonometriska ekvationer
Trigonometriska ekvationer förklaras i Exempel 2 i boken. Filmen till höger förklarar vad det handlar om.
Det trigonometriska ekvationerna har ofta flera lösningar.
Fördjupning: Här är en lösning till ekvationen sin v = o.5 i Wolfram Alpha. Den visar två lösningar till ekvationen (samt fler om man går ytterligare varv runt enhetscirkeln).
Fördjupning - Enhetscirkeln
Kunskapskontroll Ma3C - Enhetscirkeln
Öva själv
Konstigt facit: Bry er inte om bilden i facit till 1301.

