Lektion 4 - Enhetscirkeln: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) (→Övrigt) |
||
| Rad 32: | Rad 32: | ||
'''Konstigt facit:''' Bry er inte om bilden i facit till 1301. | '''Konstigt facit:''' Bry er inte om bilden i facit till 1301. | ||
{{tnkruta|Öva matte på [[Mattecentrums_räknestugor]]}} | {{tnkruta|Öva matte på [[Mattecentrums_räknestugor]]}} | ||
{{khanruta|[http://www.khanacademy.org/math/trigonometry/e/unit_circle Unit circle]}} | {{khanruta|[http://www.khanacademy.org/math/trigonometry/e/unit_circle Unit circle]}} | ||
Versionen från 1 september 2015 kl. 12.37
Det handlar om trigonometri och cirklar.
En enhetscirkel är en cirkel i planet med radie 1. Ofta talar man om enhetscirkeln och avser då en enhetscirkel med mittpunkt i origo. Av Pythagoras sats följer att enhetscirkeln kan beskrivas i kartesiska koordinater som mängden av punkter (x, y) sådana att x2 + y2 = 1. I polära koordinater blir detta den trigonometriska ettan.
För att beräkna de kartesiska koordinaterna (x, y) för en punkt på enhetscirkeln som befinner sig vid vinkeln t mätt från x-axeln kan man använda cosinus och sinus:
| Definition |
|---|
|
Texten i ovanstående avsnitt kommer från Wikipedia.se
Viktiga samband
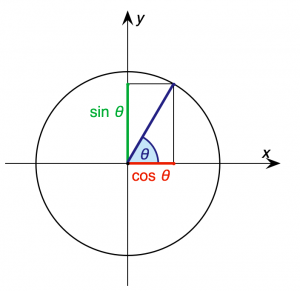
| Definition |
|---|
Speglingar i x-axeln och y-axeln
|
Fördjupning - Enhetscirkeln
Övrigt
Konstigt facit: Bry er inte om bilden i facit till 1301.

