Multiplikation och division i polär form

Repetition

[math]\displaystyle{ cos (u+v) = cos u cos v - sin u sin v }[/math]

[math]\displaystyle{ sin (u+v) = sin u cos v + cos u sin v }[/math]

[math]\displaystyle{ cos (u-v) = cos u cos v + sin u sin v }[/math]

[math]\displaystyle{ sin (u-v) = sin u cos v - cos u sin v }[/math]

Multiplikation

Vi kommer använda:

[math]\displaystyle{ cos (u+v) = cos u cos v - sin u sin v }[/math]

[math]\displaystyle{ sin (u+v) = sin u cos v + cos u sin v }[/math]

Två komplexa tal

[math]\displaystyle{ z = r (cos u + i sin u) }[/math]

[math]\displaystyle{ w = s (cos v + i sin v) }[/math]

Division med komplexa tal på polär form

Vid division av två komplexa tal dividerar men längderna på vektorerna:

[math]\displaystyle{ | \frac{z}{w} | = \frac{|z|}{|w|} }[/math]

I analogi med multiplikationen så ska man subtrahera argumenten vid division av komplexa tal:

[math]\displaystyle{ arg \frac{z}{w} = arg z - arg w }[/math]

NP-uppgift

NP MaE vt 2000 uppg 5

Np MaE ht 1999

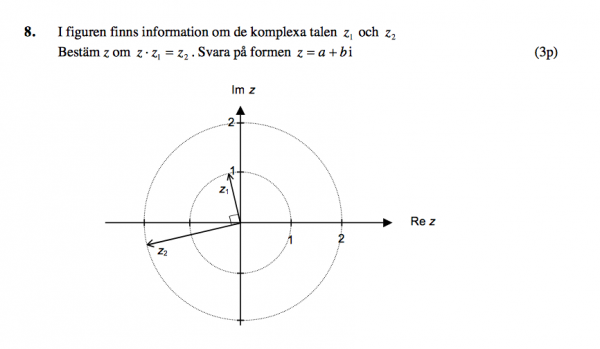
Uppgiften från Provbanken.