Rörelse Heureka: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) (→Övning) |
Hakan (diskussion | bidrag) |
||
| Rad 100: | Rad 100: | ||
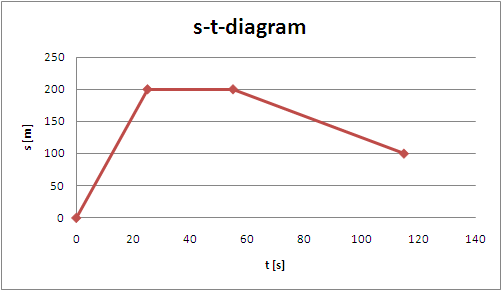
[[Fil:S-t-diagram.PNG|small|right|Sträcka-tid-diagram ser ut så här:]] | [[Fil:S-t-diagram.PNG|small|right|Sträcka-tid-diagram ser ut så här:]] | ||
=== Socrative === | |||
: vt-diagram: två frågor. Rum 282058 | |||
: You can share this quiz using SOC#: SOC-2242874 | |||
=== Repetition === | |||
Forts genomgång av extrabladet om vektorer. | |||
=== Sträcka-tid-diagram === | |||
Att utläsa hastigheten ur diagram. | Att utläsa hastigheten ur diagram. | ||
Versionen från 16 oktober 2013 kl. 11.21
Intro Rörelse
Appar
Appar som loggar sensordata:
http://www.appbrain.com/app/sensor-and-gps-monitor/org.instk.datamonitor
Intro
Wolfram Demo Galileo lutande tornet i Pisa.
Vi behöver jobba färdigt med SI-enheter, sid 21-23.
Länkar
Innehålll
Föremål i rörelse
Film
Min film men pingisbollen på Youtube: http://www.youtube.com/watch?v=OYuJXnwDPIE. Men det blir bättre med MovieMaker för där visas tiden i hundradelar.
Beskriv rörelsen med ord Beskriv diagrammet Försök Göra en kurva med hastigheten.
Förklara hur man går till väga när man räknar ut hastigheten med hjälp av mätpunkter i Excel.
Hur långt hann vi? DEDT10 han göra v-t-kurvor men vi hann inte med att diskutera dem. Ska de vara räta eller ... ? Samma ungefär med NV, dock ej vt-kurvor alls.
Ventenskapshistoria
- Nicolaus Copernicus, 19 February 1473 – 24 May 1543)
- Tycho Brahe, (14 December 1546 – 24 October 1601),
- Galileo Galilei, 15 February 1564– 8 January 1642
- Johannes Kepler, December 27, 1571 – November 15, 1630)
- Sir Isaac Newton (25 December 1642 – 20 March 172
Länkar
- http://en.wikipedia.org/wiki/Timeline_of_classical_mechanics
- http://en.wikipedia.org/wiki/Newtonian_physics
- http://en.wikipedia.org/wiki/Physics
- http://en.wikipedia.org/wiki/History_of_classical_mechanics
- http://en.wikipedia.org/wiki/Isaac_Newton
- http://sv.wikipedia.org/wiki/Isaac_Newton
Film
- Genier, Darwin, Newton, mm 88 min. Bara på dvd.
- Den rörliga jorden, 51 min.
Youtube - flippbart
- http://www.youtube.com/watch?v=-eUUHvOS0AM Läge-tid-graf (s-t-graf)
- http://www.youtube.com/watch?v=DBUjWHAOewA medelhastighet och momentanhastighet
- http://www.youtube.com/watch?v=VqzRnxn4cQo medelhastighet
- http://www.youtube.com/watch?v=9KDXOV6FtIQ likformig rörelse
- http://www.youtube.com/watch?v=uwBLQQ-nCZ8 hastighet-tid-diagram
Lektion 1 - Medelhastighet
- Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.
vm = ∆s/∆t
- Hastighet som en vektor, s 28-29.
- Fart är hur fort det går i vardagligt tal.
- Hastigheten har en storlek och en riktning. Den ritas som en vektor.
Film
- Isaac Newton och gravitationen - Milstolpar inom naturvetenskap och teknik, 15 min. Den börjar med de gamla grekerna, uppehåller sig länge vid Newton och berör Einstein.
Momentanhastighet
Intervall
Tangenten
- GGB-filen finns på GeogebraTube.
Flippa
Lektion 2 - Hastighet
Socrative
- vt-diagram: två frågor. Rum 282058
- You can share this quiz using SOC#: SOC-2242874
Repetition
Forts genomgång av extrabladet om vektorer.
Sträcka-tid-diagram
Att utläsa hastigheten ur diagram.
- ∆s
- ∆t
- vm = ∆s/∆t (som vi vet sedan tidigare)
- brantare lutning är högre hastighet
- vågrät = stillastående
- avtagande lutning betyder att färden går tillbaks
Bokens Exempel 3.5: Gå igen detta och förklara vad en tangent är. En applet förklarar
Uppgifter: Gör uppgifternas 308-312 på sidan 32. Lösning i Excel till uppgift 310
Datorövning: titta på s-t-diagrammet med pingisboleln igen.
- Excelfil med pingisdata.
- Beräkna medelhastigehten för hela resan.
- Hur ändras hastigheten under bollens färd?
Datorövning: Movin Man från PhET Colorado
Övning
Lektion 3 - Acceleration och vt-diagram


Acceleration
- Medelaccelerationen = ∆v/∆t
- ∆v = vefter-vföre
- ∆t = tefter-tföre
- Acceleration enligt Wikipedia.
- Gå igenom exempel 3.8 i boken.
Tyngdaccelerationen
- Tyngdaccelerationen är cirka 9,82 m/s2 vid jordytan. Eftersom jorden är plattare vid polerna ökar tyngdaccelerationen ju längre norrut vi kommer från ekvatorn.
v-t-diagram
- vt-graf Wikipedia.
- Här kan man jämföra st- och vt-grafer. Motsvarar Exempel 3.9 i boken.
- Lutningen i vt-diagrammet visar accelerationen:
- brantare lutning <==> större acceleration
- lutar "neråt" <==> retratado
Datorövning:
- titta på filmen med pingisboleln igen.
- Använd ditt s-t-diagrammet med pingisbollen igen till att skapa ett vt-diagram. Är rörelsen accelererad? Excelfil med pingisdata.
- Räkna ut medelaccelerationen. (Detta motsvarar exempel 3.7)
Mer att titta på:
Tre kurvor i ett diagram
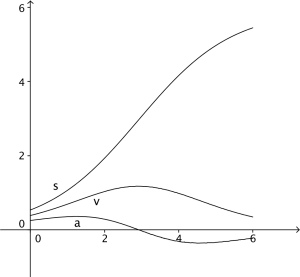
Bilden till höger har skapats genom att göra kurvanpassning med ett polynom till några punkter. Det ger en s-t-graf. Genom att derivera denna får vi v(t). Andraderivatan ger sedan a(t).
Pröva själv: Tre kurvor i denna Geogebra visar s(t), v(t) och a(t) i samma diagram: s v och a sfa t
Lösning upp 4.3-4.4
Lösning Heureka uppg 4_3-4_4 med Geogebra
Lektion 4 - Begynnelsehastighet - formler för s och v
Laborationsinstruktion: Gå igenom instruktionen till Acceleerationslabben
Begynnelsehastighet och förändring av hastigheten
Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration a, gäller då att:
v = v0 + at
v0 är hastigheten vid start och t är så klart tiden från start.
| Exempel |
|---|
| Fritt fall
Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare? t = 1,5 s. a = g = 9,82 m/s2. v0 = 0 Formel: v = v0 + at v = at = 9,82 m/s2 * 1,5 s = 14,7 m/s |
area
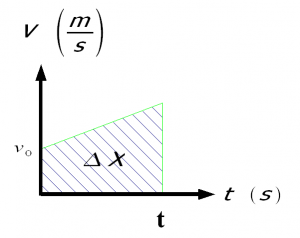
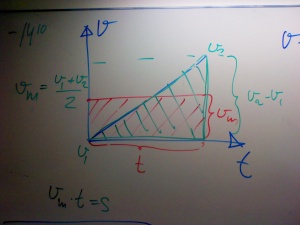
Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.
vm = (vefter + vföre) / 2
Men sträckan är ju vm * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.
naturvetenskap.org ger en beskrivning.
Animering av sträcka under vt-kurva
<swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>

sträcka
Härled uttrycket nedan som på sidan 41.
s = v0t + at2/2
härledning
s = vm t = t(v0 + v)/2 = t(v0 + v0 + at)/2 = t(2v0 + at)/2 = v0t + at2/2
| Uppgift |
|---|
| 5MBBDRYXvA8
Hur djup är brunnen? |
Räkna uppgifter
Lektion 5 - Räkneövning
Spelprogrammering och fysik
| Uppgift |
|---|
| Rörelseformler i javascript
Målet är att ni ska få ner filer i er dator och göra ändringar på dem så att ni kommer in i programmeringen och har något att jobba vidare med. Spara ner filerna 02.html och 02.js i en mapp på din dator.
|
Lektion 6 - Övningar