Regressionsanalys

Teori

Linjär regression

Regressionslinjen i blått är funktionen som bäst approximerar de röda datapunkterna

Definition

Regressionsanalys, regression, är en gren inom statistik där målet är att skapa en funktion som bäst passar observerad data. Vid enkel linjär regression utgår man från att en rät linje kan anpassas till data och regressionsekvationen är då [math]\displaystyle{ y=a+bx, \, }[/math] där y (vertikal) är den beroende (den som påverkas) variabeln och x (horisontell) är den oberoende (den som påverkar). Interceptet med y-axeln a och lutningen b beräknas så att felet jämfört med observerade data blir så litet som möjligt. Felet kan beräknas med exempelvis minstakvadratmetoden.

Linjär regression med GGB Classic

1. Använd GeoGebra Classic.
2. Skriv in dina värden i två kolumner.
3. Klicka Skapa en lista med punkter.
4. Skriv in RegressionLin(Lista_{1}) i inmatningsfönstret
5. Eventuellt behöver du högerklicka för att visa axlar.

Se exempel.

Regression i GeoGebras Grafräknare

1. Lägg in dina punkter manuellt.
2. Skapa en lista med Lista= {A,B,C,D,E,F}
3. Skriv RegressionLin(Lista)

Korrelation och kausalitet

Debatten i media (kanske i synnerhet sociala medier) innehåller många (ibland medvetna) missuppfattningar där en korrelation presenteras som ett kausalt samband.

Kausalitet handlar om orsak och verkan.

Exempel

Aktivitet

Uppgift
Pendellabb 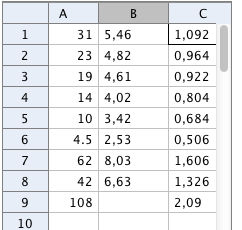Första kolumnen visar snörets längd för en pendel. I andra kolumnen visas tiden för fem svängningar. Därefter räknas svängningstiden för en svängning ut. I GGB kan man göra regression och pröva räta linjen, en andragradsfunktion och en potensfunktion. Läs mer om hur Pendeln fungerar.

Facit: Så här kan en regressionsanalys av pendeldata (i Classic) se ut. Vilken slutsats drar du?

Lär mer

Linjär regression med GGB

• http://www.geogebratube.org/student/m14559
• http://www.geogebratube.org/material/show/id/34178