Nollställe: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 49: | Rad 49: | ||
=== Uppdelning i faktorer med kvadreringsreglerna === | === Uppdelning i faktorer med kvadreringsreglerna === | ||
{{uppgruta| | {{uppgruta| | ||
Här ska vi också [[repetera kvadreringsreglerna]] med ett lösblad. | Här ska vi också '''[[repetera kvadreringsreglerna]]''' med ett lösblad. | ||
Du ska även kunna kvadreringsreglerna baklänges. | |||
Exempel: | |||
: '''1+2x+x<sup>2</sup>''' {{=}} 1(1+x)<sup>2</sup> | |||
Testa nu om du kan kvadratern med kvadreingsregeln baklänges! | |||
# '''4+8x+4x<sup>2</sup>'''{{=}} | |||
# '''4-12x+9x<sup>2</sup>'''{{=}} | |||
# '''64+144x+81x<sup>2</sup>'''{{=}} | |||
# '''0.25-10x+100x<sup>2</sup>'''{{=}} | |||
# '''a<sup>2</sup>-2ab+b<sup>2</sup>'''{{=}} | |||
# '''a<sup>2</sup>+2abx+b<sup>2</sup>x<sup>2</sup>'''{{=}} | |||
# '''0.16a<sup>2</sup>+2.4ax+9x<sup>2</sup>'''{{=}} | |||
# '''9y<sup>2</sup>-12x<sup>2</sup>y+4x<sup>4</sup>'''{{=}} | |||
}} | }} | ||
Versionen från 23 april 2018 kl. 22.26
Teori
Andragradsekvationer och rötter
| Exempel |
|---|
Lös ekvationen:
Vad händer? Pröva nu ekvationen:
här har vi en ekvation som saknar reella lösningar. |
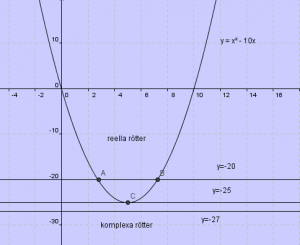
| Definition |
|---|
En andragradsekvation kan ha två reella rötter eller en dubbelrot eller två komplexa rötter |
Uppdelning i faktorer med konjugatregeln
| Uppgift |
|---|
|
Först ska vi repetera konjugatregeln med ett lösblad där det är rad snabba uppgifter. Dessa uppgifter bör klaras av på mindre än tre minuter. Sedan testar vi om du kan använda konjugatregeln baklänges. Dela upp följande uttryck i faktorer:
|
Uppdelning i faktorer med kvadreringsreglerna
| Uppgift |
|---|
|
Här ska vi också repetera kvadreringsreglerna med ett lösblad. Du ska även kunna kvadreringsreglerna baklänges. Exempel:
Testa nu om du kan kvadratern med kvadreingsregeln baklänges!
|
Aktivitet
Tempot är viktigt
Om du gör ett prov kanske det innehåller 12 uppgifter som du ska göra på en timme. Några uppgifter är lätta och går fort men några andra kräver mycket mer tid. Det ger oss anledning att fundera över hur fort man bör kunna lösa uppgifter. En rimlig hastighet är att du löser cirka 20 uppgifter per timme om uppgifterna är lagom svåra. Det innebär i snitt tre minuter per uppgift.
| Uppgift |
|---|
| Se om du kan göra en uppgift på tre minuter
Välj en uppgift i Kunskapsmatrisen på den betygsnivå som ligger nära det betyg du hade i Ma1c. Se om du kan göra uppgiften på tre minuter. Din lärare tar tid. Du ska redovisa din lösning iinom de tre minutrarna. |
Många andra Geogebras
Testa dina kunskaper om andragradsfunktioner
Bland annat Jonas Halls GGB med allt man behöver veta om andragradsfunktionens graf. Bör rensas och infogas på denna sida.
En tänkvärd övning i GeoGebra
Lär mer
|
|
|
|
|
|



