Vinklar: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) (→Teori) |
||
| Rad 7: | Rad 7: | ||
<html><script id="WolframAlphaScript" src="http://www.wolframalpha.com/input/embed/?type=small" type="text/javascript"></script></html> | <html><script id="WolframAlphaScript" src="http://www.wolframalpha.com/input/embed/?type=small" type="text/javascript"></script></html> | ||
=== Beteckning av vinklar === | |||
{{defruta| | |||
En vinkel kan betecknas på följande sätt: | |||
# grekiska bokstäver (SIS 01 61 38) | |||
# <math> \angle A</math> (efter punkten av spets A) | |||
# <math> \angle BAC</math> (efter linjerna BA och AC) | |||
# <math> \angle (c,b)</math> (efter linjerna c och b) | |||
}} | |||
=== Beräkning av vinklar === | === Beräkning av vinklar === | ||
Versionen från 17 april 2018 kl. 08.08
Teori
Beteckning av vinklar
| Definition |
|---|
|
En vinkel kan betecknas på följande sätt:
|
Beräkning av vinklar
| Definition |
|---|
Triangelns vinkelsumma
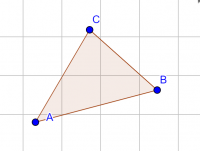 Vinkelsumman i en triangel är 180o |
| Definition |
|---|
Sidovinklar
 Sidovinklarna a och b är tillsammans 180o. |
| Definition |
|---|
| Likabelägna vinklar
|
| Definition |
|---|
Vertikalvinklar
 |
| Definition |
|---|
Alternatvinklar
 De två vinklarna är alternatvinklar. GeoGebra om Alternatvinklar mm. |
| Sats
|
Yttervinkelsatsen
 Yttervnkeln är lika stor som summan av de två motstående inre vinklarna.
Bevis: Yttervinkelsatsen Benämn den tredje vinkeln i triangeln [math]\displaystyle{ \delta }[/math]. Då gäller att:
Således är:
|
Aktivitet
Triangelns vinkelsumma
Öva vinkeldefinitioner
Extrauppgift på kul
| Uppgift |
|---|
| Kan du rita en regelbunden hexagon med hjälp av Geogebra?
 |
Lär mer
|
|
|
|
|
|
|
|
.svg)
- Malin Christersson har en fin sajt där jag hittade en Geogebra om yttervinklar.
- På engelska finns en fantastisk GeoGebra Book om Vinklar av Tim Brzezinski med teori och övningar.
Exit ticket
Gör testet nedan: