Trigonometriska ekvationer: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) (→Teori) |
||
| Rad 12: | Rad 12: | ||
{{defruta | '''Ekvationen <math>\sin(x) = a </math>''' | {{defruta | '''Ekvationen <math>\sin(x) = a </math>''' | ||
Om x = v är '''en''' llösning till ekvationen <math>\sin(x) = a </math> så '''är''' alla lösningar | Om <math>x = v</math> är '''en''' llösning till ekvationen <math>\sin(x) = a </math> så '''är''' alla lösningar | ||
<math> x = v + n \cdot 360° </math>''' | <math> x = v + n \cdot 360° </math>''' | ||
| Rad 23: | Rad 23: | ||
{{defruta | '''Ekvationen <math>\cos(x) = a </math>''' | {{defruta | '''Ekvationen <math>\cos(x) = a </math>''' | ||
Om x = v är '''en''' lösning till ekvationen <math>\cos(x) = a </math> så '''är''' alla lösningar | Om <math>x = v</math> är '''en''' lösning till ekvationen <math>\cos(x) = a </math> så '''är''' alla lösningar | ||
<math> x = +/- v + n \cdot 360° </math>''' | <math> x = +/- v + n \cdot 360° </math>''' | ||
Versionen från 1 september 2016 kl. 21.14
Teori
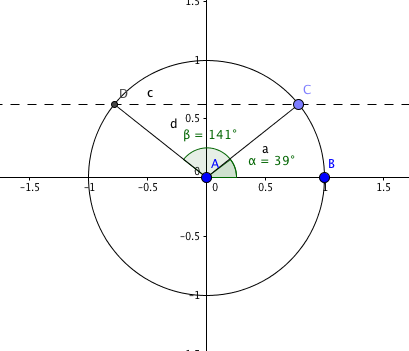
Henriks fjärde Phlipp:
| Definition |
|---|
| Ekvationen [math]\displaystyle{ \sin(x) = a }[/math]
Om [math]\displaystyle{ x = v }[/math] är en llösning till ekvationen [math]\displaystyle{ \sin(x) = a }[/math] så är alla lösningar [math]\displaystyle{ x = v + n \cdot 360° }[/math] eller [math]\displaystyle{ x = 180° - v + n \cdot 360° }[/math]
|
| Definition |
|---|
| Ekvationen [math]\displaystyle{ \cos(x) = a }[/math]
Om [math]\displaystyle{ x = v }[/math] är en lösning till ekvationen [math]\displaystyle{ \cos(x) = a }[/math] så är alla lösningar [math]\displaystyle{ x = +/- v + n \cdot 360° }[/math] |
Frågor att besvara hemma
Här är frågorna till dagens phlippp: Klicka på extrahera.
Lista: (klicka expandera till höger)
Kahoot
https://play.kahoot.it/#/k/dcf1120e-3f6c-4e14-bf05-1fc6f986c94b