Lektion 4 - Enhetscirkeln: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
Ingen redigeringssammanfattning
Rad 7: Rad 7:
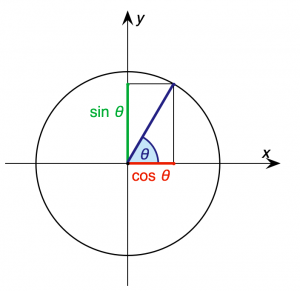
[[Fil:Unit_circle.svg|300px|right|Enhetscirkeln. Koordinaten för en punkt på cirkeln kan beräknas utifrån vinkeln ''t'' med hjälp av cosinus och sinus.]]
[[Fil:Unit_circle.svg|300px|right|Enhetscirkeln. Koordinaten för en punkt på cirkeln kan beräknas utifrån vinkeln ''t'' med hjälp av cosinus och sinus.]]


Det handlar om trigonometri och cirklar.
Dagens lektion handlar om trigonometri och cirklar. genom att titta på enhetscirkeln går vi utanför den rätvinkliga triangeln och kan arbeta med vinklar större än 90°. Genom att enhetscirklen har radien ett blir hypotenusan 1.  
 
En enhetscirkel är en cirkel i planet med radie 1. Ofta talar man om enhetscirkeln och avser då en enhetscirkel med mittpunkt i origo.
Av Pythagoras sats följer att enhetscirkeln kan beskrivas i kartesiska koordinater som mängden av punkter (x, y) sådana att x2 + y2 = 1. I polära koordinater blir detta den trigonometriska ettan.
 
För att beräkna de kartesiska koordinaterna (x, y) för en punkt på enhetscirkeln som befinner sig vid vinkeln t mätt från x-axeln kan man använda cosinus och sinus:


{{defruta |
{{defruta |

Versionen från 1 september 2015 kl. 12.52

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!
Ma3C: Enhetscirkeln, sidan 16-21
Load video
YouTube
Enhetscirkeln intro
Load video
YouTube
Enhetscirkeln del 2
Enhetscirkeln. Koordinaten för en punkt på cirkeln kan beräknas utifrån vinkeln t med hjälp av cosinus och sinus.
Enhetscirkeln. Koordinaten för en punkt på cirkeln kan beräknas utifrån vinkeln t med hjälp av cosinus och sinus.

Dagens lektion handlar om trigonometri och cirklar. genom att titta på enhetscirkeln går vi utanför den rätvinkliga triangeln och kan arbeta med vinklar större än 90°. Genom att enhetscirklen har radien ett blir hypotenusan 1.

Definition
[math]\displaystyle{ x = \cos t \qquad y = \sin t }[/math]


Texten i ovanstående avsnitt kommer från Wikipedia.se

Viktiga samband

Definition
Speglingar i x-axeln och y-axeln
[math]\displaystyle{ x = \sin (180-t = \sin t }[/math]
[math]\displaystyle{ \cos (- t) = \cos t }[/math]


Fördjupning - Enhetscirkeln

Öva själv

Tänk! Öva matte på Mattecentrums_räknestugor

Öva på Khan: Unit circle

Läxa! Lös uppgifterna 1301-1309 och gärna fler.

Konstigt facit: Bry er inte om bilden i facit till 1301.

Hämtad från ”https://wikiskola.se/index.php?title=Lektion_4_-_Enhetscirkeln&oldid=32457”