Rörelse Heureka: Skillnad mellan sidversioner

VisuellWikitext

Versionen från 30 september 2012 kl. 20.23

Lektion 4 - Intro Rörelse

Appar

Appar som loggar sensordata:

http://www.appbrain.com/app/sensor-and-gps-monitor/org.instk.datamonitor

Intro

Wolfram Demo Galileo lutande tornet i Pisa.

Vi behöver jobba färdigt med SI-enheter, sid 21-23.

Länkar

Hastighet enligt Wikipedia

Innehålll

Föremål i rörelse

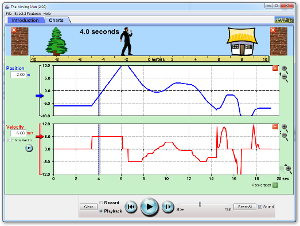
Film Min film men pingisbollen på Youtube: http://www.youtube.com/watch?v=OYuJXnwDPIE. Men det blir bättre med MovieMaker för där visas tiden i hundradelar.

Beskriv rörelsen med ord Beskriv diagrammet Försök Göra en kurva med hastigheten.

Förklara hur man går till väga när man räknar ut hastigheten med hjälp av mätpunkter i Excel.

Hur långt hann vi? DEDT10 han göra v-t-kurvor men vi hann inte med att diskutera dem. Ska de vara räta eller ... ? Samma ungefär med NV, dock ej vt-kurvor alls.

Ventenskapshistoria

Nicolaus Copernicus, 19 February 1473 – 24 May 1543)
Tycho Brahe, (14 December 1546 – 24 October 1601),
Galileo Galilei, 15 February 1564– 8 January 1642
Johannes Kepler, December 27, 1571 – November 15, 1630)
Sir Isaac Newton (25 December 1642 – 20 March 172

Länkar

Film

Genier, Darwin, Newton, mm 88 min. Bara på dvd.
Den rörliga jorden, 51 min.

Lektion 1 - Medelhastighet

Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.

v_m = ∆s/∆t

Hastighet som en vektor, s 28-29.
- Fart är hur fort det går i vardagligt tal.
- Hastigheten har en storlek och en riktning. Den ritas som en vektor.

Film

Isaac Newton och gravitationen - Milstolpar inom naturvetenskap och teknik, 15 min. Den börjar med de gamla grekerna, uppehåller sig länge vid Newton och berör Einstein.

Momentanhastighet

Intervall

Tangenten

<ggb_applet width="727" height="406" version="4.0" ggbBase64="UEsDBBQACAAIAIK2O0EAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAIK2O0EAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VndbuM2Fr6ePgWhq2QxsUlRpKSBPUVbbNEB0jYzmV0s9qIFJdE2a/1Vkh170NfZJ9kX20NSkmU7442ToJMGcSiSh+fwfOfXyuTrTZaitaxqVeRTh4ywg2QeF4nK51Nn1cyuAufrt19N5rKYy6gSaFZUmWimjqcpVTJ1ZESJy2N+FXmhuPJoJK8iP2ZXhPqeH3MSylg6CG1q9SYvfhKZrEsRy9t4ITNxXcSiMYIXTVO+GY/v7u5GnahRUc3H83k02tSJg+CaeT112oc3wG7v0B015C7GZPyvH68t+yuV143ItXytwkq9/erV5E7lSXGH7lTSLKaO7/oOWkg1X4BOjHAHjTVRCYCUMm7UWtZwdDA1OjdZ6Rgykev9V/YJpb06DkrUWiWymjp45HGf+4z6gct5wDBxUFEpmTctLWlljjtuk7WSd5atfjISPQc1RZFGQnNEf/yBXOxi9FoPxA4uDJzbLWzXMLWDawfPDszSePa4Z0k9S+NZGo86aK1qFaVy6sxEWgOCKp9VYL1+XjfbVJr7tAs77clr0KlWn4CYYnATCzmsY/xafzh8PL0x3leSDKQ21epMoZ1IY9KHinSfpCjt1fTuUdNln1GTnxBq9X6InoQNZIIo82s+RxLpKTUPJdr50wRy709RcTLuQmXSRgeqF5q29Z5GZrWOFxoiFmq3JwjiD3EfvJwhEsLguwiiARGGPAZTEiCuRx9RHzY8RFGANB2hyAQHC+CP5xtmHDFgpld9iElEQJCHGEXExJSHIJKQiUuIUZcCBWOIwSEtnriaBeXI4zCjAfLgjjokfQKEFA7CHMS7iBJE9WHiI5cjrvkRT4c6D/TVgaWLOEacaIYQ1RDRNpqBPkBUa9OlNZWXq2YPojhLusemKHtbADXko13Ws/lpLym+mqQikinUiVttSYTWItURYQTNirxBnRFduzavRLlQcX0rmwZO1eg3sRbXopGb74G67mQb2rjI65uqaL4r0lWW1wjFRYr7OxcpGTy7/a1hQgcb3nCDDTb44Nm/V24BO2hVS5BfVHVHLpLknabYpQZA8uc83X5bSbEsC7WvxmRsSs5EruJUJUrk/wRn1VI0LujeCgRFortIUSW32xo8GG3+LasCcAx9XXO3dkYJ07M6FjrEvHAUDn8CsPi23WMYCA1Tue6xFxvZqzWvVDJ8fld/W6RJr6TR6ztRNqvKNAWQ9Cp922/yeSqN7U3EQsWNl1GxubVGp5bXx20Js1Z+NDd4Ioh5lzEgaMfIjoZGX6ynwoYGGwrceZFK+n0SuobCjJEdDRW4pb1aqyjptCS4E6Nqk6mwsxcPxqd1/V7lqrnuJo2KlztNNf1PqyySvWfssyTPxHIyPvCcyVJWuUxbRwVDropVbeNu4MOJjFUGU7vRAiK0sf4BF7CriZxXsrt3atotC5fZxUMfPFo2rL6viuxdvv4InnBwgcm4u+WkjitVan9DEST3pdz5VKJqAbUhGZ7TkQWqx7oGADyNhgZibtUsCjD1D//9z1Lk6O8pNFV1o+bAA1IHUOgAS2UG/RRqjLPlq0xWKu6BF6ZVg0uuWj3oiFhNNOqoiH6DnHZgrJ1VYfsz7ohEWi6EbvBadqnYymoPKsPtxyJpBXdiU90Zokzl+jD4fyY2EKbAMKoh3zXQHINx8l1zbK/W5gvoLHTg6xMmA2wh+gP9MFMb2ccxYKY+gY+IPWV2YdFAJl5Cu1mbFqhpo9Q8/KCSROb9bUUO3mRsAsmotOoiqAPSenp/tAT1TX4YeEJrmP9roujQRNA0vyQb6Z7dGImcb6SwNVJI/lQj4UdZaVNWIE7zaUGewdfBje4LLjaXaIouBPob2lz+chFd2iZh366zVW7C19kdP23DQdoaGpEwOjCjmfWGxA80JD6BJjuF5sPd9ubQbckoeLrX7qv7hXIL563bEo8/xW9PIv1syeXIbb9p3fbi5jWaXdxcXna8TDNzn+u2G/3557XimU5rKm+t7aA9SpvBHWGXMj+g1Hc97mFg/sm+rrHvK/Ttdedl2bDh6kEBHwIXF1km8gTl5nvZR6jssO7svikIbKAUREeyVXfVdBux5dbyOAJUu0OPV/y4PPC5ZP5oOK/02xgcupz4PCC+S7luVLftiy9A9IqMSEhDQlwShPqlTdeQPyYry99ze6S2jR64ZKpi1Zw2w21alPLACPER+svT6B+mquU9FfYIiC9ScI869ofi+/A8nRwr/4K6izZH35ydoymmbZKmf/UGUB5aiHcx/gIsdNNaiJ9tITfsuj//L2Choyr6vquiia6iydlV9P2jqqh+dzi3Q2SHp+d9g8hWj5wEnAchoSwMIO0FJ+sofWAdPYbuQwed1NDJs6H78GKg6xpBOqKEETfAnss8PyCB/yzQ7de+a9007Je+97b/+HBUAedn9B/zl9J/uCMeco+FAGTohThkBls2Cm33ASAHmGHMfR86PcbxM3YfKnts9zE/7j5+JWf2H3DguANhPnZ56EPCDKhLvlBNfpYGZDx8e2Ve/bb/xXz7P1BLBwjJLgUMYwcAAGIdAABQSwECFAAUAAgACACCtjtB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAIK2O0HJLgUMYwcAAGIdAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA+gcAAAAA" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Lektion 6 - Hastighet

Repetition: Forts genomgång av extrabladet om vektorer.

Idag gör vi sid 30-32.

Sträcka-tid-diagram

Att utläsa hastigheten ur diagram.

∆s
∆t
v_m = ∆s/∆t (som vi vet sedan tidigare)
brantare lutning är högre hastighet
vågrät = stillastående
avtagande lutning betyder att färden går tillbaks

Bokens Exempel 3.5: Gå igen detta och förklara vad en tangent är. En applet förklarar

Uppgifter: Gör uppgifternas 308-312 på sidan 32. Lösning i Excel till uppgift 310

Datorövning: titta på s-t-diagrammet med pingisboleln igen.

Excelfil med pingisdata.
Beräkna medelhastigehten för hela resan.
Hur ändras hastigheten under bollens färd?

Datorövning: Movin Man från PhET Colorado

Click to Run

Lektion 7 - Acceleration och vt-diagram

Bedömningsmatrisen för densitetslabben

Planering: Vi behöver bestämma datum för laborationen om acceleration. Förslag:

TEDT10 onsdag vecka 39 kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
TEDT10  onsdag vecka 40 kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
NVNV10 tisdag kl 8-9.30 vecka 39. (NV10 ledigt)
NV10 onsdag kl 12.40-14.10 vecka 39. (NVNV10 ledigt)

v 38 Genomgång idag: neXus FYSIK sid S 33-38.

Acceleration

Medelaccelerationen = ∆v/∆t
- ∆v = v_efter-v_före
- ∆t = t_efter-t_före
Acceleration enligt Wikipedia.
Gå igenom exempel 3.8 i boken.

Tyngdaccelerationen

Tyngdaccelerationen är cirka 9,82 m/s² vid jordytan. Eftersom jorden är plattare vid polerna ökar tyngdaccelerationen ju längre norrut vi kommer från ekvatorn.

v-t-diagram

vt-graf Wikipedia.
- Här kan man jämföra st- och vt-grafer. Motsvarar Exempel 3.9 i boken.
Lutningen i vt-diagrammet visar accelerationen:
- brantare lutning <==> större acceleration
- lutar "neråt" <==> retardation

Datorövning:

titta på filmen med pingisboleln igen.
Använd ditt s-t-diagrammet med pingisbollen igen till att skapa ett vt-diagram. Är rörelsen accelererad? Excelfil med pingisdata.
Räkna ut medelaccelerationen. (Detta motsvarar exempel 3.7)

Mer att titta på:

Lektion 8 - Begynnelsehastighet - formler för s och v

v 38 Idag: Sid 39-44

Laborationsinstruktion: Gå igenom instruktionen till Acceleerationslabben

Begynnelsehastighet och förändring av hastigheten

Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration a, gäller då att:

v = v₀ + at

v₀ är hastigheten vid start och t är så klart tiden från start.

Exempel: Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare?

t = 1,5 s. a = g = 9,82 m/s². 
v = at = 9,82 m/s² * 1,5 s = 14,7 m/s

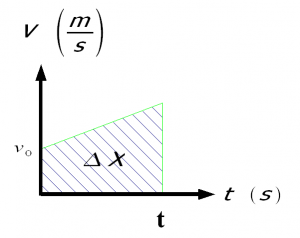
area

Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.

v_m = (v_efter - v_före) / 2

Men sträckan är ju v_m * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.

naturvetenskap.org ger en beskrivning.

Animering av sträcka under vt-kurva <swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>

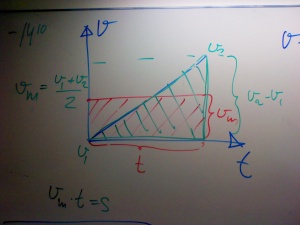
Khan om sträcka = area under vt-kurva

sträcka

Härled uttrycket nedan som på sidan 41.

s = v₀t + at²/2

Extrablad: Rörelselära ... Och Övningsuppgifter på hastighet och fart.

v 39

Sid 45-53

Uppgifter: 320-327

@@ Rad 56: / Rad 56: @@
 * [http://www.sli.se/prodinfo.asp?a=U101740-01&page=default.asp&sid=cb033b78-90a5-4d4b-9bbe-2e9e0722208e&db=4&e=videostream&g=&w=galileo&s=-1&p=1&st=0&sub=&ss=1&otyp=product&lev=&tlang=&slang= Den rörliga jorden], 51 min.
-== Lektion 5 - Medelhastighet ==
+== Lektion 1 - Medelhastighet ==
 * Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.