Matematik 3C: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
Rad 41: Rad 41:
{{lm3c|Trigonometri|10}}
{{lm3c|Trigonometri|10}}
:
:
{{Läxa|Lös mins uppgifterna 1201-1207 och gärna fler.
{{Läxa|Lös uppgifterna 1201-1207 och gärna fler.
}}
}}
{{flipp}}


=== Lektion 3 - Fasta värden ===
=== Lektion 3 - Fasta värden ===

Versionen från 28 augusti 2012 kl. 12.09

Länkar

  • Roger Bengtsson har en sajt på wikidot. Den är CC och innehåller mycket bra förklarande texter, mm.

Trigonometri

Lektion 1 - Algebra repetition

Uppgift
Repetitionstest

Skriv formler eller algebraiska förklaringar för detta:

  • kvadreringsreglerna
  • formelhantering: Vad är [math]\displaystyle{ R }[/math] om [math]\displaystyle{ I=\frac{U}{R} }[/math]
  • pq-formeln
  • Pythagoras sats


Läxa!

  • Räkna uppgifterna på sidan 9.
  • Titta även igenom innehållet till lektion 2 här på wikiskola.


Lektion 2

Load video
YouTube
Load video
YouTube
Load video
YouTube

Trigonometri grundläggande

CC By
CC Wikimedia.org

Andra länkar om trigonometri

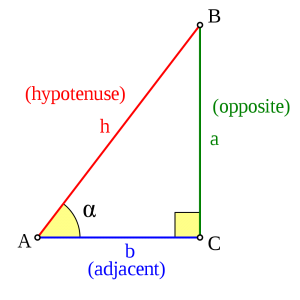
Definitioner:

  • Motstående katet
  • Närliggande katet
  • Sin v = motstående katet / hypotenusan
  • Cos v = närliggande katet / hypotenusan
  • Tangens v = motstående katet / närliggande katet

Digitalt

Definition: Ta reda på vinkeln

Om y = roten ur x så är 'y2 = x. Dessa två hänger ihop och den ena kan ses som den omvända av den andre. Detta kallas inversen, den inversa funktionen.

På samma sätt som det finns en invers funktion till kvadraten på ett tal, nämligen roten ur så finns det en invers funktion till sinus och cosinus. 

Om sin v = a/h då är v = arcsin(a/h) eller sin-1(a/h)
Om cos v = b/h då är v = arccos(b/h) eller cos-1(b/h)
0ch på samma sätt för tangens

Den rätvinkliga triangeln

rätvinklig triangel, kateter, hypotenusa

sinus

cosinus

tangens

Ma3C: Trigonometri, sidan 10

Läxa! Lös uppgifterna 1201-1207 och gärna fler.

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!


Lektion 3 - Fasta värden

Load video
YouTube

En halv liksidig triangel

En halv kvadrat

Lektion 4 - Enhetscirkeln

Load video
YouTube
Enhetscirkeln intro
Load video
YouTube
Enhetscirkeln del 2

Det handlar om trigonometri och cirklar.

malin C om Enhetscirkeln.

Lektion 5 - Triangelsatserna

Load video
YouTube
Sinussatse
Load video
YouTube
Cosinussatsen
Load video
YouTube
Areasatsen


lektion 6 Cirkelns ekvation

Här har vi en film från Youtube.

Load video
YouTube
Cirkelns ekvation

Javascript, titta på funktionen cirkel. Sid 5 i boken spelprogramering.nu.

  • Läs första sidan
  • Koden ovan anropar en funktion som heter circle och som finns i ett bibliotek på sajten spelprogrammering.nu. Undersök hur funktionen ser ut.
  • Ritas cirkeln på så sätt som i matteboken?
  • * En cirkelbåge som går 360 grader är praktiskt. Det kallas polära koordinater.
  • Kan vi gå tillväga som i funktionen för triangeln och skapa en cirkel med vår formel från matteboken?

Testa funktionen i GGB.

Derivator

Provkarta

Denna sida är ett slags provkarta på vad wikiskola har att erbjuda och visar olika typer av delar som kan ingå i en sida. Här finns bilder som ligger på wikimedia, formler som kopierats från wikipedia, filmer, GeoGebra, en quiz och en widget från Wolfram Alpha. Det finns mallar för exempel (blå), definitioner (rosa), länkar, (bruna), uppgifter, (gula), bokhänvisningar (lila), tänkare (orange) samt Khanövningar (gröna).


Embed:

<a href="https://wikiskola.se/index.php/Matematik_3C">Click to open the embedded page at Wikiskola.se</a><iframe src="https://wikiskola.se/index.php/Matematik_3C" style="width:1200px;height:800px;border:0px;" frameborder="0" scrolling="yes"></iframe>


Problemlösning med derivatan

Detta är en sammanfattning som introduktion till avsnittet om derivator. Den innehåller ett fysikproblem med en måsjägare.

3.2 Derivator

Använda derivatans definition

Deriveringsregler för polynom

Tillämpningar på derivata

3.3 Derivator och grafer

Rita kurvor med hjälp av derivatan

Största och minsta värde

Derivatans graf

Andraderivatan

Maximi- och minimiproblem

3.4 Merom derivator

Lite Algebra

Derivatan av potensfunktioner

Diskontinuerliga funktioner

Diskreta funktioner

Inflexionspunkt och derivata

Tillämpningar (ej i Liber)

Derivator kommer till användning på många områden inom naturvetenskap, ekonomi, mm. Här kommer ett exempel från fysiken.

Exempel
Tryck

Antag att [math]\displaystyle{ p(h) }[/math] betyder lufttrycket (i pascal) vid höjden [math]\displaystyle{ h }[/math] (i meter) över havsnivån. Då kommer derivatan [math]\displaystyle{ p'(h) }[/math] att ange hur mycket trycket ökar per meter i höjdled. Derivatan får alltså den fysikaliska enheten pascal per meter. Eftersom trycket i själva verket avtar med höjden, kommer alltså derivatan att bli negativ.

Texten i ovanstående avsnitt kommer från Wikipedia.se


Derivataquiz

1 Derivatan av 2x3 är:

x2
3x2
6x2
x3/3

2 Derivatan beskriver hur något förändras.

Sannt.
Falskt.

3 Derivatan anger hur krokig en kurva är.

Sannt.
Falskt.

4  

Den svarta kurvan illustrerar en godtyckligt vald funktion.
Vad kallas den röda linjen?

5 Förändringen mellan två punkter ges av att [math]\displaystyle{ {\Delta y = 200} }[/math] och [math]\displaystyle{ {\Delta x = 3} }[/math]. Vad blir lutningen?



Läs mer:
  1. Bruno Kevius om derivatan
  2. Matteboken Matte C har innehåll om derivator
  3. Matteboken Matte D
  4. GGB-övningar i mängder. A-nivå


Prov

Integraler

Kan man tänka sig någon trevlig frågeställning som ingång till integralerna?

Hämtad från ”https://wikiskola.se/index.php?title=Matematik_3C&oldid=15791”