Procent år 7: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| (112 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
== | == planer == | ||
* [[Terminsplan matte år 7 vt]] | * [[Terminsplan matte år 7 vt]] | ||
* [[Kursplan_i_procent_som_anpassats_för_år_7|Kursplan]] | * [[Kursplan_i_procent_som_anpassats_för_år_7|Kursplan]] | ||
'''Inledning''' | '''Inledning''' | ||
| Rad 9: | Rad 8: | ||
* Läxor som vanligt men även en klurig hemuppgift som alternativ. | * Läxor som vanligt men även en klurig hemuppgift som alternativ. | ||
{{procent_introduktion_ar_7}} | |||
{{Bråk_decimal_procentform}} | |||
{{Hur_mycket_är_x_procent_av_något}} | |||
{{procentandelen}} | |||
{{Räkna_mer_med_procent}} | |||
{{Procentformeln}} | |||
{{Procent_Kunskapskontroll_m_Forms}} | |||
{{Procent_Förändring}} | |||
== Lektion 10 - Över G2 == | |||
Extrauppgifter på papper eller här: | |||
* [[Media:Forforstaelsetest_procent_ak_7.doc|Förförståelsetest]] procent åk 7. | |||
* Gammalt [[Media:Prov_procent_ak7.doc|procentprov]] nr 1. | |||
{{Procent_Repetition}} | |||
== Lektion 12 - Prov == | |||
== Lektion | |||
Nuvarande version från 20 maj 2011 kl. 11.01
planer
Inledning
- Läxor som vanligt men även en klurig hemuppgift som alternativ.
Lektion 1 - Introduktion Procent
Testa vad du kan redan
Ladda om sidan om du inte ser frågorna.
Det här testet bygger på en sida i Google Drive. När alla har gjort testet kan ni titta på statistiken och diskutera vad ni behöver öva på.
Svara på frågorna och tryck på Submit när du är klar.
Se resultatet genom att expandera rutan
Här ser vi resultatet. Vi kommer att projicera det på tavlan så vi kan diskutera det.
Det ser tyvärr ut som att jag måste vara inloggad för att se resultaten trots att jag har delat filen.
Här är kalkylarket där man kan nollställa resultatet genom att ta bort svarsraderna i tabellen.
Lär dig grunderna om procent
Lektion 2 - procentbegreppet
Förstå procentbegreppet.
Teori: Vad är procent 1?
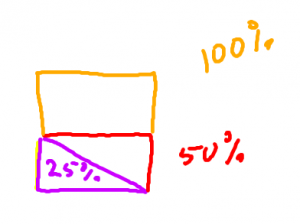
Procent betyder hundradelar. procent är att dela det hela i hundra delar. Här ser du att det egentligen är samma sak som bråk.
Lektion 3 - bråk-, decimal, procentform
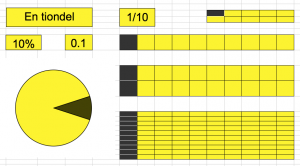
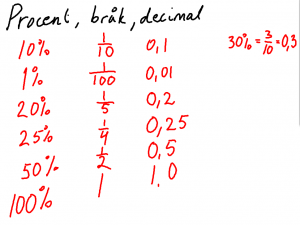
Mål: Kunna utföra omvandlingar mellan tal i bråkform och tal i decimalform till procentform.
Omvandlingar mellan bråk-, decimal- och procentform. Procent är bråk. Det vet vi sen tidigare. men hundradelar är decimaltal, 0.01. Så procent är även decimaltal
Data. matteva om procent-, decimal- och bråkform
Excel: Bilden med en tiondel i olika gulsvarta representationer kommer från en Excelfil som heter Procent_som_bilder.xlsx. Kanske vill du prova att skapa en egen bild av något annat procenttal.
lektion 4 - Enkla procenttal
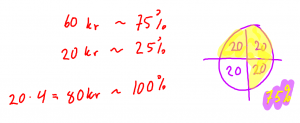
Mål: Behärska 100, 50, 25, 20, 10 %
Mål: kunna göra enklare procentberäkningar i huvudet
Teori: Räkna med procent 1
Utgå ifrån de kända procenttalen och deras motsvarigheter i bråkform.
exempel. Om du vet att tio procent är en tiondel. Då är 10% av 200 = 20. Då vet du också att 30 % av 200 är 60 (3*20)
Samma sak med hundradelar En procent av 350 är 3,50. 4% av 350 är 4 * 3,50 = 14.
Teori: Räkna med procent 2
Tag procenten * det hela och dela med 100
vad är 10 % av 400? 400/100 = 4. 10 * 4 = 40. Svar: 40.
'
Film
Exempelvis lär vi oss att räkna ut 4 % av 120 i denna film: Martin Procent 1
Data. matteva har en övning med procentrutor som är ganska fiffig om man fastnar för den eller helt knäpp om man inte gillar den. Försök klura ut vad du tycker.
Uppgift 2: Gruppuppgift. Hälften och hälften igen. Arbetsblad 4:7 (Andelar i %) från Lärarhandledningen till matteDirekt år 7.
Lektion 5 - beräkna procent av något
Kunna beräkna hur mycket _____% är av något.
Webbmatte: Läs och begrunda Vi söker delen
Formel. Delen = Andelen * det hela
Uppgift.
- Gruppuppgift. Procentspel. Arbetsblad 4:8 från MD. Ett papper per elev så att ni kan läsa instruktionen men ni bör spela på samma plan. Lärarhandledning till Procentspel.
- Färglägg en matteruta från lektion.se som finns uppkopierad på papper.
- PPT. Presentation om procenträkning med två olika sätt att förkorta bort nollor och sätta decimaler.
- En uppgift från ett Nigeriabrev.
Lektion 6 - Räkna ut hur många procent det är
Mål. kunna beräkna procenttalet då delen och helheten är givna
Teori: Vad är procent 2?
Vad är procent om man ser till den praktiska användningen?
Formel: andelen = delen / det hela
Bondestam återkommer med en formel för procenträkningen:
Centikuber och procent
Hur många procent är rosa? Laboration. Du får en näven centikuber av olika färg. Ta reda på hur många procent av dessa som är rosa. Om du inte har centikuber kan du be eleverna titta på denna flipchart.
Detta är en praktisk övning som börjar med en presentation. Sedan får du en näve centikuber i olika färger. uppgiften är att beräkan andelen rosa och ange detta som ett procenttal. Titta på presentationen först och testa sedan. Det är lätt!
Presentationen ligger inbäddad bredvid om man snabbt vill titta igenom den men eftersom den är animerad kan det vara roligare att köra powerpointfilen Centikuber och procent2.
Gör en egen undersökning om procenten
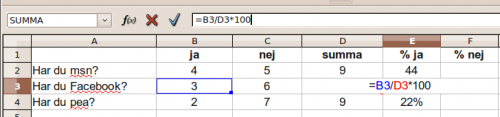
- Gruppuppgift. Gör en undersökning där du ställer frågot till ett antal kompisar. Frågorna hittar du på själv. Det ska vara frågor som är av typen Ja/Nej eller där man kan svara rätt eller fel. Hitta på omkring tio frågor. frågorna kan gärna höra till ett tema, exemelvis sport , ordkunskap, matematik, film eller liknade. Sedan gör du en tabell i Excel och skriver in dina värden. Du kan låta Excel räkna ut procenten åt dig men det får din lärare visa dig. En exempelfil finns här.
Procent på E-nivå
Här är en presentation av grunderna i procenträkning. Du får en genomgång av de olika sätten att tänka för att förstå procent. När du förstått detta kommer du förmodligen at använda dig av en formel för att räkna ut procentuppgifter. Mer om detta snart.
Det finns några saker som behöver en kommunikativ förbättring. I så fall ligger filen här: Powerpoint: Procent genomgång grunder2
Lektion 7 - Räkna mer med procent: decimaltal och multiplikation
Nu ska vi lära oss den metod som de flesta vuxna användernär de räknar procent i vardagliga livet. Det händer att elever säger "Varför sa du inte det här med en gång" när de får reda på detta. En didaktisk tankeställare för oss lärare.
Presentationen till höger finns för nedladdning här: Procent 2 varianter
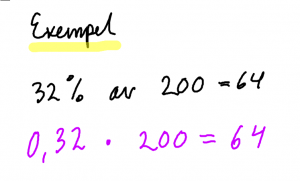
Mål: Kunna göra beräkningar med procent.
Teori: Räkna med procent 3
gör om procent till ett decimaltal. Multiplicera (gärna med miniräknare)
32 % av 200 kr = 0,32 * 200 kr = 64 kr
Tillåt miniräknare på provet. Jag menar ... de kluriga uppgifterna är ju ändå svåra. de klurigaste uppgifterna är kanske att räkna procent 1...
Film
Här kommer först Mikael Bondestam och förklarar hur man räknar ut procent på de två vanligaste sätten, dels genom att multiplicera med ett decimaltal och dels genom att ta ett enklare procenttal.
Om frågan är vad 20 % av 50 kr är kan man dels ta 0,20 * 50 = 10 eller tänka 10 % innebär 50 / 10 = 5 kr och sedan ta 2 * 5 = 10 kr (vilket då är 20 %).

Mikael Bondestam om skillnaden mellan procent och procentenheter.
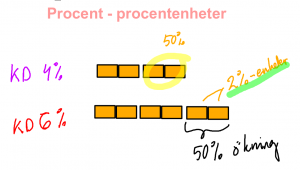
Övningsuppgift på procent - procentenheter
- Det är skillnad på procent och procentenheter
- Om vi tänker oss att miljöpartiet ökar från 8% till 10% i en undersökning av väljarsympatier då kan man uttrycka ökningen på två sätt.
- 1 Miljöpartiet har ökat med 2 procentenheter
- 2 Miljöpartiet har ökat med 25%
- Fundera en stund och förklara hur det här hänger ihop.
Lektion 8 - Överkurs om procentformeln

Vi har ju tidigare stött på uttrycket andelen = delen / det hela. om man förstått och lärt sig det uttrycket har man stor nytta av att kunna modifiera algebraiska uttryck. Det finns några regler som gäller för vaad man kan göra för att förändra ett uttryck utan att förstöra sambandet. uttrycket om andel är egentligen tre uttryck i ett. Som det ser ut nu visar det hur man kan räkna ut andelen. men om man vrder på uttrycket kan man använda det för att räkna ut delen. Eller Det hela. tricket är att skriva om uttrycket så att rätt ord kommer för likhetstecknet.
Denna flipchart berättar hur man kan stuva om i formler och hur det används på andelen-formeln.
Vänd på uttrycket andelen = delen / det hela.
Då blir uttrycket: det hela = delen / andelen
exempel. Du vet att 4 motsvara 20 % Hur mycket är det hela? använd ekvationen 0,20 = 4 / x <==> x = 4 / 0,20
Jämför med det traditionella sättet att räkna enligt Räkna med procent 1.
Ex.: Om 4 motsvarar 20 % så gäller att 2 motsvarar 10 % och då får vi att 20 motsvarar 100 %
Alternativ. Man ser kanske att 20 % är en femtedel. Då är det bara att multiplicera 4 med 5.
Det viktiga här är att inse att man kan göra på flera olika sätt men att de senare lämpar sig bäst för huvudräkning med enklare tal. Med siffror från verkliga uppgifter går det oftast inte jämnt ut och då lämpar sig ekvationslösningen och dator/miniräknare bäst.
Övning - Momsberäkningar
- Du vet att det är 25% moms på en vara som man köper i affären men om du köper in saker i ett företag så anges priset ex moms (utan moms). Tänk dig att köpt en vara för 50 kr (ex moms). Hur mycket ska du lägga på för att få priset inkl moms?
- Det är inte 25%, varför?
Kunskapskontroll med Google Forms
Klicka på länken och svara på frågorna. tryck Submit / Skicka när du är klar. Ladda om sidan ifall formuläret inte syns.
Det här testet kan eleverna göra och sedan kan man titta på statistiken över svaren och diskutera vad man behöver arbeta mer med i gruppen.
Se resultatet genom att expandera rutan
Här ser vi resultatet. Vi kommer att projicera det på tavlan så vi kan diskutera det.
Här är kalkylarket där man kan nollställa resultatet genom att ta bort svarsraderna i tabellen. Nollställ innan du kör detta med en ny elevgrupp.
Jag kan redigera frågorna här.--Håkan Elderstig 2 november 2012 kl. 23.06 (UTC)
Lektion 9 - Över G
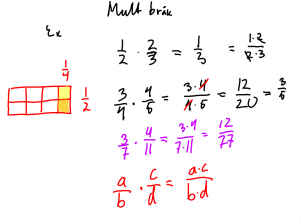
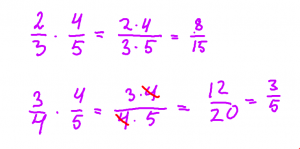
MD År 8
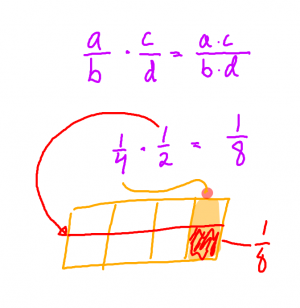
Det kan vara lämpligt att ta upp multiplikation av bråk sid 150, förändringsfaktor s 164, upprepade förändringar s 165, ekvationer s 166, division av bråk s 169-171.
Över G. Kunna räkna med förändring.
Över G: Kunna räkna med upprepad förändring.
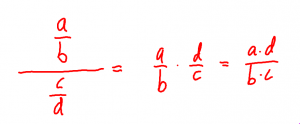
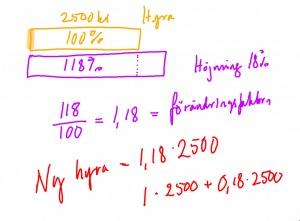
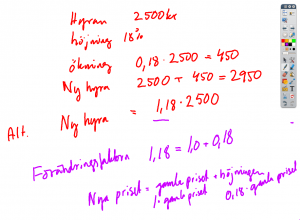
Procent på procent
- Antag att vi har en vara som från början kostar 200 kr.
- Priset på varan höjs fyra gånger med 5%.
- Hur mycket kostar varan då?
- Det handlar om en höjning i taget så det innebär inte en höjning med 4*5 = 20%.
- Hur kan det se ut. Visa med ett exempel
- Egentligen fungerar det lika dant oavsett vad ursprungspriset är. Kalla ursprungspriset för x och försök skapa ett uttryck för priset efter höjningarna.
- Pröva att generalisera uttrycket ytterligare. Kalla räntan för r. hur ser uttrycket ut nu?
Lektion 10 - Över G2
Extrauppgifter på papper eller här:
- Förförståelsetest procent åk 7.
- Gammalt procentprov nr 1.
Lektion 11 - repetition
Repetitionsuppgifter: Nu är det dags att dela ut repetitionsfrågor till kap 7 och 8. Dessutom kan det finnas gamla prov att öva på.
Om provet
Det är ok att använda miniräknare på provets B-del. Vi har bland annat lärt oss metoden att omvandla procent till decimalform och multoplicera med det hela. Detta fungerar i alla sammanhang och är anpassat för att använda miniräknare.
- PPT Presentation med sammanfattning av grunderna i procenräkning.
- Det finns en definition av procentbegreppet på svenska Wikipedia. Den är värd att läsa för att den är lite mer teoretisk än vad du finner i matteboken.
- Jag kan rekommendera att en genomläsning av hela denna sida på wikiskola om procent.
