Sin 3x = cos 2x: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| (11 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
[[Category:Matematik]] [[Category:Ma4]] [[Category:Aritmetik, algebra och geometri]] [[Category:Trigonometri]] | |||
== Flippa teorin nedan == | == Flippa teorin nedan == | ||
{{ | {{flipped | Denna gång ska du titta på en algebraisk lösning}} | ||
{{lm4| sin 3x = cos 2x | 43-44 }} | {{lm4| sin 3x = cos 2x | 43-44 }} | ||
{{uppgruta | Försök lösa ekvationen <math>\sin(3x) = \cos(2x)</math> | |||
<br /> | |||
Vilka svårigheter kan du förutse? | |||
En ledtråd finner du i figuren nedan. | |||
}} | |||
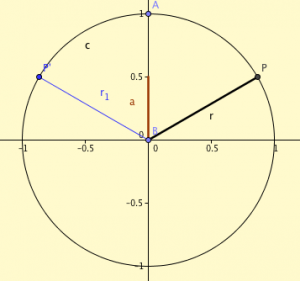
[[Fil:Sinus i enhetscirkel.png|miniatyr|Sinus för vinkeln motsvarar höjden på y-axeln. Det finns två vinklar som ger samma värde, alfa och 180° - alfa.]] | [[Fil:Sinus i enhetscirkel.png|miniatyr|Sinus för vinkeln motsvarar höjden på y-axeln. Det finns två vinklar som ger samma värde, alfa och 180° - alfa.]] | ||
<html><iframe scrolling="no" src="https://www.geogebra.org/material/iframe/id/snVumJPn/width/244/height/207/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/auto" width="244px" height="207px" style="border:0px;"> </iframe></html> | |||
=== Lösning === | === Lösning === | ||
| Rad 32: | Rad 42: | ||
=== Lösning med grafritande hjälpmedel === | === Lösning med grafritande hjälpmedel === | ||
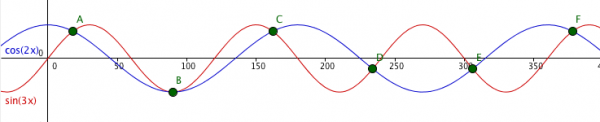
[[Fil:Sin 3x eq cos 2x.png| | [[Fil:Sin 3x eq cos 2x.png| 600px |Grafisk lösning till Sin 3x = cos 2x]] | ||
Rita de två funktionerna y = sin 3x respektive y = cos 2x och finn skärningspunkterna. | Rita de två funktionerna y = sin 3x respektive y = cos 2x och finn skärningspunkterna. | ||
{{clear}} | |||
== Svara på frågorna nedan == | == Svara på frågorna nedan == | ||
Svara på frågorna i formuläret nedan så vet vi vad du kan och vad du kan behöva diskutera mer eller repetera. | Svara på frågorna i formuläret nedan så vet vi vad du kan och vad du kan behöva diskutera mer eller repetera. | ||
{{Lista | | |||
<html> | |||
<iframe src="https://docs.google.com/forms/d/1LsS_gTbIPWMgaAWcJkw6DFuULON_MQJwtG_Y15snIsE/viewform?embedded=true" width="760" height="500" frameborder="0" marginheight="0" marginwidth="0">Loading...</iframe> | |||
</html> | |||
}} | |||
Nuvarande version från 5 september 2016 kl. 20.34
Flippa teorin nedan
| Uppgift |
|---|
| Försök lösa ekvationen [math]\displaystyle{ \sin(3x) = \cos(2x) }[/math]
En ledtråd finner du i figuren nedan. |
Lösning
Denna gång ingen film men du får förbereda dig genom att titta på denna förklaring (förenkling av den i boken).
Vi ska allts lösa ekvationen sin 3x = cos 2x
Repetition: Vi vet sen tidigare att cos x = sin (90°-x)
Alltså kan vi skriva skriva att cos 2x = sin (90°-2x)
Sätt in det i ekvationen ger sin 3x = sin (90-2x)
Den enkla lösningen ges av att
- 3x = 90 - 2x + n 360°
- 5x = 90 + n 360°
- x = 18 + n 72°
Den andra (inte lika uppenbara) lösningen får vi om tänker på att punkten på enhetscirkel som speglas i y-axeln också är en lösning. Det är alltså 180° minus vinkeln, se figur.
- 3x = 180 - (90 - 2x) + n 360° ( uttrycket inom parentesen är samma som i den enkla lösningen.
- 3x = 180 - 90 + 2x + n 360°
- x = 90 + n 360°
Lösningarna är x = 18, 90, 162, 234, ....
Lösning med grafritande hjälpmedel
Rita de två funktionerna y = sin 3x respektive y = cos 2x och finn skärningspunkterna.
Svara på frågorna nedan
Svara på frågorna i formuläret nedan så vet vi vad du kan och vad du kan behöva diskutera mer eller repetera.
Lista: (klicka expandera till höger)