Rörelse Heureka: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
 
(112 mellanliggande sidversioner av samma användare visas inte)
Rad 55: Rad 55:
* [http://www.sli.se/prodinfo.asp?a=DVD%20%20181&page=default.asp&sid=e77cc91b-06d8-4c05-a115-d1e735218d1c&db=4&e=&g=&w=galileo&s=-1&p=1&st=0&sub=&ss=1&otyp=product&lev=&tlang=&slang= Genier, Darwin, Newton, mm] 88 min. Bara på dvd.
* [http://www.sli.se/prodinfo.asp?a=DVD%20%20181&page=default.asp&sid=e77cc91b-06d8-4c05-a115-d1e735218d1c&db=4&e=&g=&w=galileo&s=-1&p=1&st=0&sub=&ss=1&otyp=product&lev=&tlang=&slang= Genier, Darwin, Newton, mm] 88 min. Bara på dvd.
* [http://www.sli.se/prodinfo.asp?a=U101740-01&page=default.asp&sid=cb033b78-90a5-4d4b-9bbe-2e9e0722208e&db=4&e=videostream&g=&w=galileo&s=-1&p=1&st=0&sub=&ss=1&otyp=product&lev=&tlang=&slang= Den rörliga jorden], 51 min.
* [http://www.sli.se/prodinfo.asp?a=U101740-01&page=default.asp&sid=cb033b78-90a5-4d4b-9bbe-2e9e0722208e&db=4&e=videostream&g=&w=galileo&s=-1&p=1&st=0&sub=&ss=1&otyp=product&lev=&tlang=&slang= Den rörliga jorden], 51 min.
== Youtube - flippbart ==
* http://www.youtube.com/watch?v=DBUjWHAOewA medelhastighet och momentanhastighet
* http://www.youtube.com/watch?v=VqzRnxn4cQo medelhastighet
* http://www.youtube.com/watch?v=9KDXOV6FtIQ likformig rörelse
* http://www.youtube.com/watch?v=uwBLQQ-nCZ8 hastighet-tid-diagram
* http://www.youtube.com/watch?feature=player_detailpage&v=z_k6LaoponE st, vt, at och frit fall
== Flippa st-grafen ==
{{flipped|
{{#ev:youtube |-eUUHvOS0AM|340 }}
: [http://www.youtube.com/watch?v{{=}}-eUUHvOS0AM Läge-tid-graf (s-t-graf)]
}}
== Läge-tid-grafen ==


== Lektion 1 - Medelhastighet ==
== Lektion 1 - Medelhastighet ==


{{Heureka|Sidorna 66-75.
}}
* Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.
* Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.
  v<sub>m</sub> = ∆s/∆t
  v<sub>m</sub> = ∆s/∆t
Rad 73: Rad 93:
=== Tangenten ===
=== Tangenten ===


<ggb_applet width="727" height="406"  version="4.0" ggbBase64="UEsDBBQACAAIAIK2O0EAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAIK2O0EAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VndbuM2Fr6ePgWhq2QxsUlRpKSBPUVbbNEB0jYzmV0s9qIFJdE2a/1Vkh170NfZJ9kX20NSkmU7442ToJMGcSiSh+fwfOfXyuTrTZaitaxqVeRTh4ywg2QeF4nK51Nn1cyuAufrt19N5rKYy6gSaFZUmWimjqcpVTJ1ZESJy2N+FXmhuPJoJK8iP2ZXhPqeH3MSylg6CG1q9SYvfhKZrEsRy9t4ITNxXcSiMYIXTVO+GY/v7u5GnahRUc3H83k02tSJg+CaeT112oc3wG7v0B015C7GZPyvH68t+yuV143ItXytwkq9/erV5E7lSXGH7lTSLKaO7/oOWkg1X4BOjHAHjTVRCYCUMm7UWtZwdDA1OjdZ6Rgykev9V/YJpb06DkrUWiWymjp45HGf+4z6gct5wDBxUFEpmTctLWlljjtuk7WSd5atfjISPQc1RZFGQnNEf/yBXOxi9FoPxA4uDJzbLWzXMLWDawfPDszSePa4Z0k9S+NZGo86aK1qFaVy6sxEWgOCKp9VYL1+XjfbVJr7tAs77clr0KlWn4CYYnATCzmsY/xafzh8PL0x3leSDKQ21epMoZ1IY9KHinSfpCjt1fTuUdNln1GTnxBq9X6InoQNZIIo82s+RxLpKTUPJdr50wRy709RcTLuQmXSRgeqF5q29Z5GZrWOFxoiFmq3JwjiD3EfvJwhEsLguwiiARGGPAZTEiCuRx9RHzY8RFGANB2hyAQHC+CP5xtmHDFgpld9iElEQJCHGEXExJSHIJKQiUuIUZcCBWOIwSEtnriaBeXI4zCjAfLgjjokfQKEFA7CHMS7iBJE9WHiI5cjrvkRT4c6D/TVgaWLOEacaIYQ1RDRNpqBPkBUa9OlNZWXq2YPojhLusemKHtbADXko13Ws/lpLym+mqQikinUiVttSYTWItURYQTNirxBnRFduzavRLlQcX0rmwZO1eg3sRbXopGb74G67mQb2rjI65uqaL4r0lWW1wjFRYr7OxcpGTy7/a1hQgcb3nCDDTb44Nm/V24BO2hVS5BfVHVHLpLknabYpQZA8uc83X5bSbEsC7WvxmRsSs5EruJUJUrk/wRn1VI0LujeCgRFortIUSW32xo8GG3+LasCcAx9XXO3dkYJ07M6FjrEvHAUDn8CsPi23WMYCA1Tue6xFxvZqzWvVDJ8fld/W6RJr6TR6ztRNqvKNAWQ9Cp922/yeSqN7U3EQsWNl1GxubVGp5bXx20Js1Z+NDd4Ioh5lzEgaMfIjoZGX6ynwoYGGwrceZFK+n0SuobCjJEdDRW4pb1aqyjptCS4E6Nqk6mwsxcPxqd1/V7lqrnuJo2KlztNNf1PqyySvWfssyTPxHIyPvCcyVJWuUxbRwVDropVbeNu4MOJjFUGU7vRAiK0sf4BF7CriZxXsrt3atotC5fZxUMfPFo2rL6viuxdvv4InnBwgcm4u+WkjitVan9DEST3pdz5VKJqAbUhGZ7TkQWqx7oGADyNhgZibtUsCjD1D//9z1Lk6O8pNFV1o+bAA1IHUOgAS2UG/RRqjLPlq0xWKu6BF6ZVg0uuWj3oiFhNNOqoiH6DnHZgrJ1VYfsz7ohEWi6EbvBadqnYymoPKsPtxyJpBXdiU90Zokzl+jD4fyY2EKbAMKoh3zXQHINx8l1zbK/W5gvoLHTg6xMmA2wh+gP9MFMb2ccxYKY+gY+IPWV2YdFAJl5Cu1mbFqhpo9Q8/KCSROb9bUUO3mRsAsmotOoiqAPSenp/tAT1TX4YeEJrmP9roujQRNA0vyQb6Z7dGImcb6SwNVJI/lQj4UdZaVNWIE7zaUGewdfBje4LLjaXaIouBPob2lz+chFd2iZh366zVW7C19kdP23DQdoaGpEwOjCjmfWGxA80JD6BJjuF5sPd9ubQbckoeLrX7qv7hXIL563bEo8/xW9PIv1syeXIbb9p3fbi5jWaXdxcXna8TDNzn+u2G/3557XimU5rKm+t7aA9SpvBHWGXMj+g1Hc97mFg/sm+rrHvK/Ttdedl2bDh6kEBHwIXF1km8gTl5nvZR6jssO7svikIbKAUREeyVXfVdBux5dbyOAJUu0OPV/y4PPC5ZP5oOK/02xgcupz4PCC+S7luVLftiy9A9IqMSEhDQlwShPqlTdeQPyYry99ze6S2jR64ZKpi1Zw2w21alPLACPER+svT6B+mquU9FfYIiC9ScI869ofi+/A8nRwr/4K6izZH35ydoymmbZKmf/UGUB5aiHcx/gIsdNNaiJ9tITfsuj//L2Choyr6vquiia6iydlV9P2jqqh+dzi3Q2SHp+d9g8hWj5wEnAchoSwMIO0FJ+sofWAdPYbuQwed1NDJs6H78GKg6xpBOqKEETfAnss8PyCB/yzQ7de+a9007Je+97b/+HBUAedn9B/zl9J/uCMeco+FAGTohThkBls2Cm33ASAHmGHMfR86PcbxM3YfKnts9zE/7j5+JWf2H3DguANhPnZ56EPCDKhLvlBNfpYGZDx8e2Ve/bb/xXz7P1BLBwjJLgUMYwcAAGIdAABQSwECFAAUAAgACACCtjtB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAIK2O0HJLgUMYwcAAGIdAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA+gcAAAAA" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
<html>
<iframe scrolling="no" src="http://www.geogebratube.org/material/iframe/id/52977/width/727/height/364/border/888888/rc/false/ai/false/sdz/false/smb/false/stb/false/stbh/true/ld/false/sri/false/at/preferhtml5" width="727px" height="364px" style="border:0px;"> </iframe>
</html>
 
 
 
: GGB-filen finns på [http://www.geogebratube.org/material/show/id/52977 GeogebraTube].
 
== Flippa ==
{{flipped|
{{#ev:youtube | DgkQ9uf0Qi8 | 340 }}
: http://www.youtube.com/watch?v{{=}}DgkQ9uf0Qi8 hastighet tid (v-t-graf)
}}


== Lektion 2 - Hastighet ==
== Lektion 2 - Hastighet ==
{{Heureka|Sidorna 76-80.
}}
[[Fil:S-t-diagram.PNG|small|right|Sträcka-tid-diagram ser ut så här:]]
=== Socrative ===


[[Fil:S-t-diagram.PNG|small|right|Sträcka-tid-diagram ser ut så här:]]
: [http://m.socrative.com/student/#joinRoom Socrative] vt-diagram: två frågor. Rum 282058
: You can share this quiz using SOC#: SOC-2242874


'''Repetition:''' Forts genomgång av extrabladet om vektorer.
=== Repetition ===


'''Idag ''' gör vi sid 30-32.
Forts genomgång av extrabladet om vektorer.  


'''Sträcka-tid-diagram'''
=== Sträcka-tid-diagram ===


Att utläsa hastigheten ur diagram.
Att utläsa hastigheten ur diagram.
Rad 105: Rad 143:


<html><div style="position: relative; width: 300px; height: 226px;"><a href="http://phet.colorado.edu/sims/moving-man/moving-man_en.jnlp" style="text-decoration: none;"><img src="http://phet.colorado.edu/sims/moving-man/moving-man-screenshot.png" alt="The Moving Man" style="border: none;" width="300" height="226"/><div style="position: absolute; width: 200px; height: 80px; left: 50px; top: 73px; background-color: #FFF; opacity: 0.6; filter: alpha(opacity = 60);"></div><table style="position: absolute; width: 200px; height: 80px; left: 50px; top: 73px;"><tr><td style="text-align: center; color: #000; font-size: 24px; font-family: Arial,sans-serif;">Click to Run</td></tr></table></a></div></html>
<html><div style="position: relative; width: 300px; height: 226px;"><a href="http://phet.colorado.edu/sims/moving-man/moving-man_en.jnlp" style="text-decoration: none;"><img src="http://phet.colorado.edu/sims/moving-man/moving-man-screenshot.png" alt="The Moving Man" style="border: none;" width="300" height="226"/><div style="position: absolute; width: 200px; height: 80px; left: 50px; top: 73px; background-color: #FFF; opacity: 0.6; filter: alpha(opacity = 60);"></div><table style="position: absolute; width: 200px; height: 80px; left: 50px; top: 73px;"><tr><td style="text-align: center; color: #000; font-size: 24px; font-family: Arial,sans-serif;">Click to Run</td></tr></table></a></div></html>
<br />
=== Övning ===
<html>
<iframe scrolling="no" src="http://www.geogebratube.org/material/iframe/id/53001/width/1065/height/343/border/888888/rc/false/ai/false/sdz/false/smb/false/stb/false/stbh/true/ld/false/sri/false/at/preferhtml5" width="800px" height="343px" style="border:0px;"> </iframe>
</html>
<br />
<br />


== Lektion 3 - Acceleration och vt-diagram ==
== Lektion 3 - Acceleration och vt-diagram ==
[[File:Falling ball.jpg|200px|right|Falling ball]]


'''Bedömningsmatrisen''' för densitetslabben
{{Heureka|Sidorna 81-83.
}}
[[Fil:Acceleration.svg|thumb|left|250px|Den blå kurvan i vt-diagramet visar hastighetens förändring. Tangenten används för att beräkna accelerationen i den punkt där den gröna linjen tangerar den blå hastighetsgrafen.]]
[[Fil:Falling ball.jpg|200px|right|Falling ball]]


'''Planering:''' Vi behöver bestämma datum för laborationen om acceleration. Förslag:
=== Acceleration ===
TEDT10 onsdag vecka '''39''' kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
TEDT10  onsdag vecka '''40''' kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
NVNV10 tisdag kl 8-9.30 vecka '''39'''. (NV10 ledigt)
NV10 onsdag kl 12.40-14.10 vecka '''39'''. (NVNV10 ledigt)


<font color=green>v 38</font color=green>
'''Genomgång idag: ''' neXus FYSIK sid S 33-38.
'''Acceleration'''
* Medelaccelerationen = ∆v/∆t
* Medelaccelerationen = ∆v/∆t
** ∆v = v<sub>efter</sub>-v<sub>före</sub>
** ∆v = v<sub>efter</sub>-v<sub>före</sub>
Rad 128: Rad 167:
* Gå igenom exempel 3.8 i boken.
* Gå igenom exempel 3.8 i boken.


'''Tyngdaccelerationen'''
=== Tyngdaccelerationen ===
 
* Tyngdaccelerationen är cirka 9,82 m/s<sup>2</sup> vid jordytan. Eftersom jorden är plattare vid polerna ökar tyngdaccelerationen  ju längre norrut vi kommer från ekvatorn.
* Tyngdaccelerationen är cirka 9,82 m/s<sup>2</sup> vid jordytan. Eftersom jorden är plattare vid polerna ökar tyngdaccelerationen  ju längre norrut vi kommer från ekvatorn.


'''v-t-diagram''' 
==== v-t-diagram ====
 
* [http://en.wikipedia.org/wiki/Velocity_vs._time_graph vt-graf Wikipedia].
* [http://en.wikipedia.org/wiki/Velocity_vs._time_graph vt-graf Wikipedia].
** Här kan man jämföra st- och vt-grafer. Motsvarar Exempel 3.9 i boken.
** Här kan man jämföra st- och vt-grafer. Motsvarar Exempel 3.9 i boken.
* Lutningen i vt-diagrammet visar accelerationen:
* Lutningen i vt-diagrammet visar accelerationen:
** brantare lutning <==> större acceleration
** brantare lutning <==> större acceleration
** lutar "neråt" <==> retardation
** lutar "neråt" <==> retratado
 


'''Datorövning:'''
{{uppgruta| '''Datorövning'''
<youtube>OYuJXnwDPIE</youtube>  
<youtube>OYuJXnwDPIE</youtube>  
* titta på filmen med pingisboleln igen.  
* titta på filmen med pingisboleln igen.  
* Hämta data här: [[media:Rullande_pingisboll_övningsdata.xlsx| Excelfil med mätdata]]
* Använd ditt s-t-diagrammet med pingisbollen igen till att skapa ett vt-diagram. Är rörelsen accelererad? [[Media:Demonstration_med_pingisboll3.xls|Excelfil med pingisdata]].
* Använd ditt s-t-diagrammet med pingisbollen igen till att skapa ett vt-diagram. Är rörelsen accelererad? [[Media:Demonstration_med_pingisboll3.xls|Excelfil med pingisdata]].
* Räkna ut medelaccelerationen. (Detta motsvarar exempel 3.7)
* Räkna ut medelaccelerationen. (Detta motsvarar exempel 3.7)
 
}}
{{khanruta|Se filmen om acceleration
{{khanruta|Se filmen om acceleration
[http://www.khanacademy.org/science/physics/mechanics/v/acceleration?playlist Khan Academy om acceleration]
[http://www.khanacademy.org/science/physics/mechanics/v/acceleration?playlist Khan Academy om acceleration]
Rad 153: Rad 194:
* [http://www.georgiostheodoridis.se/archives/FyAstgrafMedelhastMomentHast.html Georgios smedja i matematik och fysik].
* [http://www.georgiostheodoridis.se/archives/FyAstgrafMedelhastMomentHast.html Georgios smedja i matematik och fysik].


== Lektion 8 - Begynnelsehastighet - formler för s och v ==
{{läxa|Läs sidorna i boken
: Lös uppgifterna 4.20-4.29
}}
 
=== Tre kurvor i ett diagram ===
[[Fil:S_v_t_som_regression_m_s-kurva.png|right|300px|Bilden visar tre grafer. överst är st-grafen, sedan ligger vt-grafen och underst ser du at-grafen]]
 
Bilden till höger har skapats genom att göra kurvanpassning med ett polynom till några punkter. Det ger en s-t-graf. Genom att derivera denna får vi v(t). Andraderivatan ger sedan a(t).
 
'''Pröva själv:''' Tre kurvor i denna Geogebra visar s(t), v(t) och a(t) i samma diagram: [[s v och a sfa t]]
<br />
{{clear}}
 
==== Lösning upp 4.3-4.4 ====
 
[[Lösning Heureka uppg 4_3-4_4 med Geogebra]]
 
== Flippa Fritt fall ==
{{flipped|
{{#ev:youtube | doD_I2X4jtk | 340 }}
:  [http://www.youtube.com/watch?v{{=}}doD_I2X4jtk PolhemsJocke: Fysik 1 Fritt fall och acceleration]
}}
 
== Tracker videoanalys av fritt fallande boll ==
 
* [[Tracker/Fallande boll|Fallande boll]]


== Lektion 4 - Begynnelsehastighet - formler för s och v ==
{{Heureka|Sidorna 84-90.
}}
[[Fil:Trapez_vt.png|thumb|Sträckan = arean under en vt-graf. CC By Tharbad]]
[[Fil:Trapez_vt.png|thumb|Sträckan = arean under en vt-graf. CC By Tharbad]]
<font color=green>v 38 </font color=green>'''Idag:''' Sid 39-44


'''Laborationsinstruktion:''' Gå igenom instruktionen till Acceleerationslabben
'''Laborationsinstruktion:''' Gå igenom instruktionen till Acceleerationslabben


'''Begynnelsehastighet och förändring av hastigheten'''
=== Begynnelsehastighet och förändring av hastigheten ===


Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration ''a'', gäller då att:
Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration ''a'', gäller då att:
Rad 168: Rad 235:
''v<sub>0</sub>'' är hastigheten vid start och ''t'' är så klart tiden från start.
''v<sub>0</sub>'' är hastigheten vid start och ''t'' är så klart tiden från start.


Exempel: Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare?
{{Exruta|'''Fritt fall'''
  t = 1,5 s. a = g = 9,82 m/s<sup>2</sup>.  
Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare?
  v = at = 9,82 m/s<sup>2</sup> * 1,5 s = 14,7 m/s
  t <nowiki>=</nowiki> 1,5 s.
a <nowiki>=</nowiki> g <nowiki>=</nowiki> 9,82 m/s<sup>2</sup>.  
  v<sub>0</sub> <nowiki>=</nowiki> 0
'''Formel''':  v <nowiki>=</nowiki> v<sub>0</sub> + at
v <nowiki>=</nowiki> at <nowiki>=</nowiki> 9,82 m/s<sup>2</sup> * 1,5 s <nowiki>=</nowiki> 14,7 m/s
}}


'''area'''
=== area ===


Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.
Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.
  v<sub>m</sub> = (v<sub>efter</sub> - v<sub>före</sub>) / 2  
  v<sub>m</sub> = (v<sub>efter</sub> + v<sub>före</sub>) / 2  
Men sträckan är ju v<sub>m</sub> * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.
Men sträckan är ju v<sub>m</sub> * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.


[http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=87&Itemid=94 naturvetenskap.org ger en beskrivning.]
[http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=87&Itemid=94 naturvetenskap.org ger en beskrivning.]


'''Animering av sträcka under vt-kurva'''
=== Animering av sträcka under vt-kurva ===
<swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>
<swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>


Rad 187: Rad 260:
[[Fil:FysikA_320.jpg|thumb|uppgift 320 b, c, d]]
[[Fil:FysikA_320.jpg|thumb|uppgift 320 b, c, d]]


[http://www.khanacademy.org/video/why-distance-is-area-under-velocity-time-line?playlist=Physics Khan om sträcka = area under  vt-kurva]
{{khanruta|'''Se filmen!'''
[http://www.khanacademy.org/video/why-distance-is-area-under-velocity-time-line Khan om sträcka <nowiki>=</nowiki> area under  vt-kurva]
}}


'''sträcka'''
=== sträcka ===


Härled uttrycket nedan som på sidan 41.
Härled uttrycket nedan som på sidan 41.
  s = v<sub>0</sub>t + at<sup>2</sup>/2
  s = v<sub>0</sub>t + at<sup>2</sup>/2


'''Extrablad:''' Rörelselära ...  Och Övningsuppgifter på hastighet och fart.
==== härledning ====


<font color=green>v 39</font color=green>
s = v<sub>m</sub> t = t(v<sub>0</sub> + v)/2 = t(v<sub>0</sub> + v<sub>0</sub> + at)/2 = t(2v<sub>0</sub> + at)/2 = v<sub>0</sub>t + at<sup>2</sup>/2


Sid 45-53
=== Fritt fall i önskebrunn på Tom Tits ===


'''Uppgifter''': 320-327
{{:onskebrunnen}}
 
=== Räkna uppgifter ===
 
{{läxa|Läs sidorna i boken, sid 96
: Lös uppgifterna i Heureka: 4.30-4.31
}}
 
== Lektion 5 - Räkneövning ==
 
{{TIS|Åke Dahllöf|
* '''Uppgift 1:''' [[Media:Övningsuppgift_på_hastighet_och_fart.pdf|Övningsuppgift_på_hastighet_och_fart]]
* '''Uppgift 2:''' [[Media:Uppgifter_på_rörelseformlerna.pdf|Uppgifter_på_rörelseformlerna]]
* '''Uppgift 3:''' [[Media:Sammanställning_av_rörelselagarna.pdf|Sammanställning_av_rörelselagarna‎]]
* '''Uppgift 4:''' [[Media:Rörelselära_demouppgifter.pdf|Rörelselära_demouppgifter‎]]
}}
 
=== Spelprogrammering och fysik ===
{{jspel|Idag gör vi kapitel 9.1 i boken Spelprogrammering och fysik. i
: http://spelprogrammering.nu
}}
{{uppgruta|'''Rörelseformler i javascript'''
 
'''Målet''' är att ni ska få ner filer i er dator och göra ändringar på dem så att ni kommer in i programmeringen och har något att jobba vidare med.
 
Spara ner filerna 02.html och 02.js i en mapp på din dator.
* Pröva att göra ändringar av bollens färg och storlek.
* Ändra värdet för g och se vad som händer
* Vad är det för formel som styr bollens rörelse? Var känner du igen den ifrån?
}}
 
== Lektion 6 - Övningar ==
{{Heureka|Sidorna 91-96.
}}
{{tnkruta |
Jonathan har två bollar vilka han döpt till Δs och Δt. Vad blir deras hastighet om Δs är täljare och Δt är nämnare?
}}
{{clear}}

Nuvarande version från 11 augusti 2015 kl. 07.42

Intro Rörelse

Appar

Appar som loggar sensordata:

http://www.appbrain.com/app/sensor-and-gps-monitor/org.instk.datamonitor

Intro

Wolfram Demo Galileo lutande tornet i Pisa.

Vi behöver jobba färdigt med SI-enheter, sid 21-23.

Länkar

Hastighet enligt Wikipedia


Innehålll

Föremål i rörelse


Film Min film men pingisbollen på Youtube: http://www.youtube.com/watch?v=OYuJXnwDPIE. Men det blir bättre med MovieMaker för där visas tiden i hundradelar.

Beskriv rörelsen med ord Beskriv diagrammet Försök Göra en kurva med hastigheten.

Förklara hur man går till väga när man räknar ut hastigheten med hjälp av mätpunkter i Excel.

Hur långt hann vi? DEDT10 han göra v-t-kurvor men vi hann inte med att diskutera dem. Ska de vara räta eller ... ? Samma ungefär med NV, dock ej vt-kurvor alls.

Ventenskapshistoria

  • Nicolaus Copernicus, 19 February 1473 – 24 May 1543)
  • Tycho Brahe, (14 December 1546 – 24 October 1601),
  • Galileo Galilei, 15 February 1564– 8 January 1642
  • Johannes Kepler, December 27, 1571 – November 15, 1630)
  • Sir Isaac Newton (25 December 1642 – 20 March 172

Länkar

Film

Youtube - flippbart

Flippa st-grafen

Flippa = Gör detta till nästa lektion!

Load video
YouTube
Läge-tid-graf (s-t-graf)


Läge-tid-grafen

Lektion 1 - Medelhastighet

NoK Heureka Fysik 1: Sidorna 66-75.

  • Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.
vm = ∆s/∆t
  • Hastighet som en vektor, s 28-29.
    • Fart är hur fort det går i vardagligt tal.
    • Hastigheten har en storlek och en riktning. Den ritas som en vektor.

Film

Momentanhastighet

Intervall

Tangenten


GGB-filen finns på GeogebraTube.

Flippa

Flippa = Gör detta till nästa lektion!

Load video
YouTube
http://www.youtube.com/watch?v=DgkQ9uf0Qi8 hastighet tid (v-t-graf)


Lektion 2 - Hastighet

NoK Heureka Fysik 1: Sidorna 76-80.

Sträcka-tid-diagram ser ut så här:
Sträcka-tid-diagram ser ut så här:

Socrative

Socrative vt-diagram: två frågor. Rum 282058
You can share this quiz using SOC#: SOC-2242874

Repetition

Forts genomgång av extrabladet om vektorer.

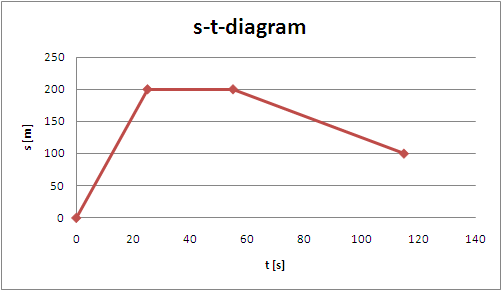
Sträcka-tid-diagram

Att utläsa hastigheten ur diagram.

  • ∆s
  • ∆t
  • vm = ∆s/∆t (som vi vet sedan tidigare)
  • brantare lutning är högre hastighet
  • vågrät = stillastående
  • avtagande lutning betyder att färden går tillbaks

Bokens Exempel 3.5: Gå igen detta och förklara vad en tangent är. En applet förklarar

Uppgifter: Gör uppgifternas 308-312 på sidan 32. Lösning i Excel till uppgift 310

Datorövning: titta på s-t-diagrammet med pingisboleln igen.

  1. Excelfil med pingisdata.
  2. Beräkna medelhastigehten för hela resan.
  3. Hur ändras hastigheten under bollens färd?

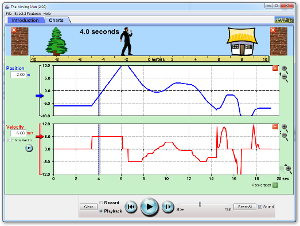
Datorövning: Movin Man från PhET Colorado

The Moving Man
Click to Run


Övning



Lektion 3 - Acceleration och vt-diagram

NoK Heureka Fysik 1: Sidorna 81-83.

Den blå kurvan i vt-diagramet visar hastighetens förändring. Tangenten används för att beräkna accelerationen i den punkt där den gröna linjen tangerar den blå hastighetsgrafen.
Falling ball
Falling ball

Acceleration

Tyngdaccelerationen

  • Tyngdaccelerationen är cirka 9,82 m/s2 vid jordytan. Eftersom jorden är plattare vid polerna ökar tyngdaccelerationen ju längre norrut vi kommer från ekvatorn.

v-t-diagram

  • vt-graf Wikipedia.
    • Här kan man jämföra st- och vt-grafer. Motsvarar Exempel 3.9 i boken.
  • Lutningen i vt-diagrammet visar accelerationen:
    • brantare lutning <==> större acceleration
    • lutar "neråt" <==> retratado
Uppgift
Datorövning
Load video
YouTube
  • titta på filmen med pingisboleln igen.
  • Hämta data här: Excelfil med mätdata
  • Använd ditt s-t-diagrammet med pingisbollen igen till att skapa ett vt-diagram. Är rörelsen accelererad? Excelfil med pingisdata.
  • Räkna ut medelaccelerationen. (Detta motsvarar exempel 3.7)
Öva på Khan: Se filmen om acceleration

Khan Academy om acceleration


Mer att titta på:

Läxa! Läs sidorna i boken

Lös uppgifterna 4.20-4.29


Tre kurvor i ett diagram

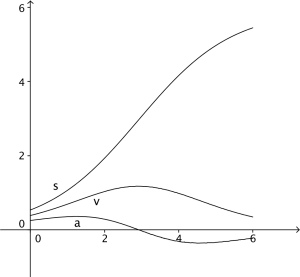
Bilden visar tre grafer. överst är st-grafen, sedan ligger vt-grafen och underst ser du at-grafen
Bilden visar tre grafer. överst är st-grafen, sedan ligger vt-grafen och underst ser du at-grafen

Bilden till höger har skapats genom att göra kurvanpassning med ett polynom till några punkter. Det ger en s-t-graf. Genom att derivera denna får vi v(t). Andraderivatan ger sedan a(t).

Pröva själv: Tre kurvor i denna Geogebra visar s(t), v(t) och a(t) i samma diagram: s v och a sfa t

Lösning upp 4.3-4.4

Lösning Heureka uppg 4_3-4_4 med Geogebra

Flippa Fritt fall

Flippa = Gör detta till nästa lektion!

Load video
YouTube
PolhemsJocke: Fysik 1 Fritt fall och acceleration


Tracker videoanalys av fritt fallande boll

Lektion 4 - Begynnelsehastighet - formler för s och v

NoK Heureka Fysik 1: Sidorna 84-90.

Sträckan = arean under en vt-graf. CC By Tharbad

Laborationsinstruktion: Gå igenom instruktionen till Acceleerationslabben

Begynnelsehastighet och förändring av hastigheten

Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration a, gäller då att: 

v = v0 + at

v0 är hastigheten vid start och t är så klart tiden från start.

Exempel
Fritt fall

Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare? 

t = 1,5 s.
a = g = 9,82 m/s2. 
v0 = 0

Formel:  v = v0 + at
v = at = 9,82 m/s2 * 1,5 s = 14,7 m/s


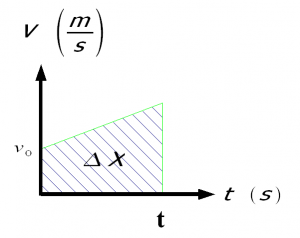
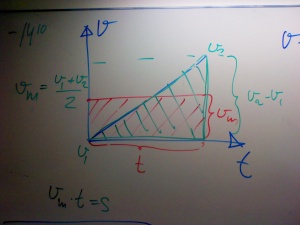
area

Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan. 

vm = (vefter + vföre) / 2

Men sträckan är ju vm * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.

naturvetenskap.org ger en beskrivning.

Animering av sträcka under vt-kurva

<swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>

uppgift 320 b, c, d
Öva på Khan: Se filmen!

Khan om sträcka = area under vt-kurva


sträcka

Härled uttrycket nedan som på sidan 41. 

s = v0t + at2/2

härledning

s = vm t = t(v0 + v)/2 = t(v0 + v0 + at)/2 = t(2v0 + at)/2 = v0t + at2/2

Fritt fall i önskebrunn på Tom Tits

Önskebrunnen på Tom Tits

Load video
YouTube

Beräkning av djupet 

s = at2/2

Vi hjälps åt med att ta tid. Genom att beräkna medelvärdet får vi bättre noggrannhet.

Mätning av djupet

En annan metod är att ta ett måttband och mäta djupet. Det visade att brunnen var ungefär 5 m djup.

Räkna uppgifter

Läxa! Läs sidorna i boken, sid 96

Lös uppgifterna i Heureka: 4.30-4.31


Lektion 5 - Räkneövning

Åke Dahllöf har skapat och delar


Spelprogrammering och fysik

Javascript och spel Kod: CC By SA spelprogrammering.nu

Idag gör vi kapitel 9.1 i boken Spelprogrammering och fysik. i

http://spelprogrammering.nu
Uppgift
Rörelseformler i javascript

Målet är att ni ska få ner filer i er dator och göra ändringar på dem så att ni kommer in i programmeringen och har något att jobba vidare med.

Spara ner filerna 02.html och 02.js i en mapp på din dator.

  • Pröva att göra ändringar av bollens färg och storlek.
  • Ändra värdet för g och se vad som händer
  • Vad är det för formel som styr bollens rörelse? Var känner du igen den ifrån?


Lektion 6 - Övningar

NoK Heureka Fysik 1: Sidorna 91-96.

Tänk! Jonathan har två bollar vilka han döpt till Δs och Δt. Vad blir deras hastighet om Δs är täljare och Δt är nämnare?

Hämtad från ”https://wikiskola.se/index.php?title=Rörelse_Heureka&oldid=32341”